Read the manual below or download the PDF.
SHARC: Surface Hopping in the Adiabatic Representation Including Arbitrary Couplings-Manual
Contents
1 Introduction
1.1 Capabilities
1.1.1 New features in SHARC Version 2.0
1.1.2 New features in SHARC Version 2.1
1.1.3 New features in SHARC Version 2.1.1
1.1.4 New features in SHARC Version 3.0
1.2 References
1.3 Authors
1.4 Suggestions and Bug Reports
1.5 Notation in this Manual
2 Installation
2.1 How To Obtain
2.2 Terms of Use
2.3 Installation
2.3.1 WFOVERLAP Program
2.3.2 Libraries
2.3.3 Test Suite
2.3.4 Additional Programs
2.3.5 Quantum Chemistry Programs
3 Execution
3.1 Running a single trajectory
3.1.1 Input files
3.1.2 Running the dynamics code
3.1.3 Output files
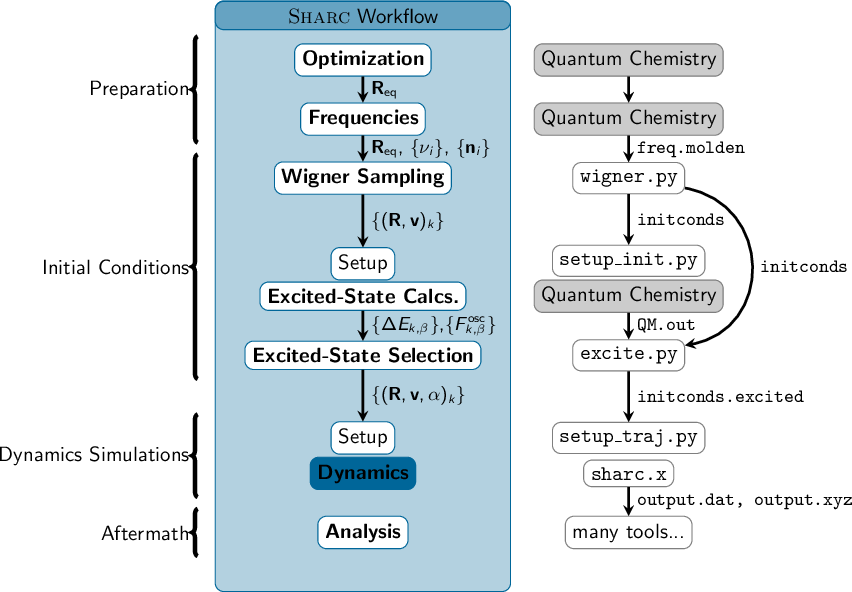
3.2 Typical workflow for an ensemble of trajectories
3.2.1 Initial condition generation
3.2.2 Running the dynamics simulations
3.2.3 Analysis of the dynamics results
3.3 Auxilliary Programs and Scripts
3.3.1 Setup
3.3.2 Analysis
3.3.3 Interfaces
3.3.4 Others
3.4 The PYSHARC dynamics driver
4 Input files
4.1 Main input file
4.1.1 General remarks
4.1.2 Input keywords
4.1.3 Detailed Description of the Keywords
4.1.4 Example
4.2 Geometry file
4.3 Velocity file
4.4 Coefficient file
4.5 Laser file
4.6 Atom mask file
4.7 RATTLE file
5 Output files
5.1 Log file
5.2 Listing file
5.3 Data file
5.3.1 Specification of the data file
5.4 Data file in NetCDF format
5.5 XYZ file
6 Interfaces
6.1 Interface Specifications
6.1.1 QM.in Specification
6.1.2 QM.out Specification
6.1.3 Further Specifications
6.1.4 Save Directory Specification
6.2 Overview over Interfaces
6.2.1 Example Directory
6.3 MOLPRO Interface
6.3.1 Template file: MOLPRO.template
6.3.2 Resource file: MOLPRO.resources
6.3.3 Error checking
6.3.4 Things to keep in mind
6.3.5 Molpro input generator: molpro_input.py
6.4 MOLCAS Interface
6.4.1 Template file: MOLCAS.template
6.4.2 Resource file: MOLCAS.resources
6.4.3 Template file generator: molcas_input.py
6.4.4 QM/MM key file: MOLCAS.qmmm.key
6.4.5 QM/MM connection table file: MOLCAS.qmmm.table
6.5 COLUMBUS Interface
6.5.1 Template input
6.5.2 Resource file: COLUMBUS.resources
6.5.3 Template setup
6.6 Analytical PESs Interface
6.6.1 Parametrization
6.6.2 Template file: Analytical.template
6.7 ADF Interface
6.7.1 Template file: ADF.template
6.7.2 Resource file: ADF.resources
6.7.3 QM/MM force field file: ADF.qmmm.ff
6.7.4 QM/MM connection table file: ADF.qmmm.table
6.7.5 Input file generator: ADF_input.py
6.7.6 Frequencies converter: ADF_freq.py
6.8 RICC2 Interface
6.8.1 Template file: RICC2.template
6.8.2 Resource file: RICC2.resources
6.8.3 QM/MM force field file
6.8.4 QM/MM connection table file: RICC2.qmmm.table
6.9 LVC Interface
6.9.1 Input files
6.9.2 Template File Setup: wigner.py, setup_LVCparam.py, and create_LVCparam.py
6.10 GAUSSIAN Interface
6.10.1 Template file: GAUSSIAN.template
6.10.2 Resource file: GAUSSIAN.resources
6.11 ORCA Interface
6.11.1 Template file: ORCA.template
6.11.2 Resource file: ORCA.resources
6.11.3 QM/MM force field file
6.11.4 QM/MM connection table file: ORCA.qmmm.table
6.12 BAGEL Interface
6.12.1 Template file: BAGEL.template
6.12.2 Resource file: BAGEL.resources
6.13 The WFOVERLAP Program
6.13.1 Installation
6.13.2 Workflow
6.13.3 Calling the program
6.13.4 Input data
6.13.5 Output
7 Auxilliary Scripts
7.1 Wigner Distribution Sampling: wigner.py
7.1.1 Usage
7.1.2 Normal mode types
7.1.3 Non-default masses
7.1.4 Sampling at finite temperatures
7.1.5 Output
7.2 Vibrational State Selected Sampling: state_selected.py
7.2.1 Usage
7.2.2 Major options
7.2.3 Normal mode types
7.2.4 Non-default masses
7.2.5 Output
7.3 AMBER Trajectory Sampling: amber_to_initconds.py
7.3.1 Usage
7.3.2 Time Step
7.3.3 Atom Types and Masses
7.3.4 Output
7.4 SHARC Trajectory Sampling: sharctraj_to_initconds.py
7.4.1 Usage
7.4.2 Random Picking of Time Step
7.4.3 Output
7.5 Setup of Initial Calculations: setup_init.py
7.5.1 Usage
7.5.2 Input
7.5.3 Interface-specific input
7.5.4 Input for Run Scripts
7.5.5 Output
7.6 Excitation Selection: excite.py
7.6.1 Usage
7.6.2 Input
7.6.3 Matrix diagonalization
7.6.4 Output
7.6.5 Specification of the initconds.excited file format
7.7 Setup of Trajectories: setup_traj.py
7.7.1 Input
7.7.2 Interface-specific input
7.7.3 Output control
7.7.4 Run script setup
7.7.5 Output
7.8 Laser field generation: laser.x
7.8.1 Usage
7.8.2 Input
7.9 Calculation of Absorption Spectra: spectrum.py
7.9.1 Input
7.9.2 Output
7.9.3 Error Analysis
7.10 File transfer: retrieve.sh
7.11 Data Extractor: data_extractor.x
7.11.1 Usage
7.11.2 Output
7.12 Data Extractor for NetCDF: data_extractor_NetCDF.x
7.12.1 Usage
7.12.2 Output
7.13 Data Converter for NetCDF: data_converter.x
7.13.1 Usage
7.13.2 Output
7.14 Plotting the Extracted Data: make_gnuscript.py
7.15 Ensemble Diagnostics Tool: diagnostics.py
7.15.1 Usage
7.15.2 Input
7.16 Calculation of Ensemble Populations: populations.py
7.16.1 Usage
7.16.2 Output
7.17 Calculation of Numbers of Hops: transition.py
7.17.1 Usage
7.18 Fitting population data to kinetic models: make_fit.py
7.18.1 Usage
7.18.2 Input
7.18.3 Output
7.19 Fitting population data to kinetic models: make_fitscript.py
7.19.1 Usage
7.19.2 Input
7.19.3 Output
7.20 Estimating Errors of Fits: bootstrap.py
7.20.1 Usage
7.20.2 Input
7.20.3 Output
7.21 Obtaining Special Geometries: crossing.py
7.21.1 Usage
7.21.2 Output
7.22 Internal Coordinates Analysis: geo.py
7.22.1 Input
7.22.2 Options
7.23 Essential Dynamics Analysis: trajana_essdyn.py
7.23.1 Usage
7.23.2 Input
7.23.3 Output
7.24 Normal Mode Analysis: trajana_nma.py
7.24.1 Usage
7.24.2 Input
7.24.3 Output
7.25 General Data Analysis: data_collector.py
7.25.1 Usage
7.25.2 Input
7.25.3 Output
7.26 Optimizations: orca_External and setup_orca_opt.py
7.26.1 Usage
7.26.2 Input
7.26.3 Output
7.26.4 Description of orca_External
7.27 Single Point Calculations: setup_single_point.py
7.27.1 Usage
7.27.2 Input
7.27.3 Output
7.28 Format Data from QM.out Files: QMout_print.py
7.28.1 Usage
7.28.2 Output
7.29 Diagonalization Helper: diagonalizer.x
8 Methods and Algorithms
8.1 Absorption Spectrum
8.2 Active and inactive states
8.3 Amdahl’s Law
8.4 Bootstrapping for Population Fits
8.5 Computing electronic populations
8.6 Damping
8.7 Decoherence
8.7.1 Energy-based decoherence
8.7.2 Augmented FSSH decoherence
8.8 Essential Dynamics Analysis
8.9 Excitation Selection
8.9.1 Excitation Selection with Diabatization
8.10 Global fits and kinetic models
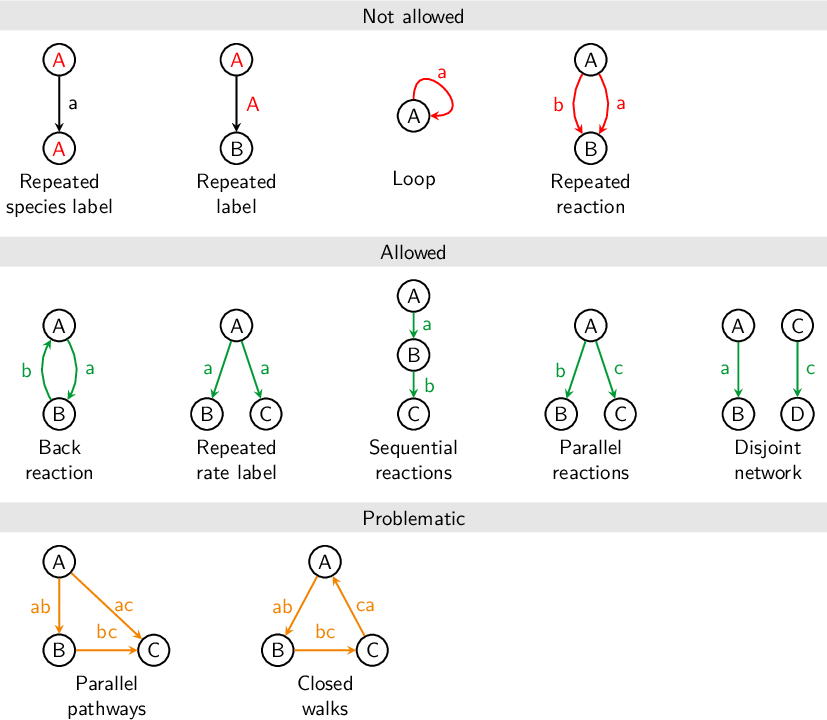
8.10.1 Reaction networks
8.10.2 Kinetic models
8.10.3 Global fit
8.11 Gradient transformation
8.11.1 Nuclear gradient tensor transformation scheme
8.11.2 Time derivative matrix transformation scheme
8.11.3 Dipole moment derivatives
8.12 Internal coordinates definitions
8.13 Kinetic energy adjustments
8.13.1 Reflection for frustrated hops
8.13.2 Choices of momentum adjustment direction
8.14 Projection operator
8.15 Fewest switches with time uncertainty
8.16 Laser fields
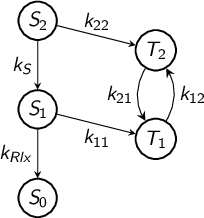
8.16.1 Form of the laser field
8.16.2 Envelope functions
8.16.3 Field functions
8.16.4 Chirped pulses
8.16.5 Quadratic chirp without Fourier transform
8.17 Laser interactions
8.17.1 Surface Hopping with laser fields
8.18 Linear Vibronic Coupling Models
8.18.1 Obtaining LVC parameters from ab initio data
8.19 Normal Mode Analysis
8.20 Optimization of Crossing Points
8.21 Phase tracking
8.21.1 Phase tracking of the transformation matrix
8.21.2 Tracking of the phase of the MCH wave functions
8.22 Random initial velocities
8.23 Representations
8.23.1 Current state in MCH representation
8.24 Sampling from Wigner Distribution
8.24.1 Sampling at Non-zero Temperature
8.25 Scaling
8.26 Seeding of the RNG
8.27 Selection of gradients and nonadiabatic couplings
8.28 State ordering
8.29 Surface Hopping
8.30 Self-Consistent Potential Methods
8.31 Effective Nonadiabatic Coupling Vector
8.32 Velocity Verlet
8.33 Wavefunction propagation
8.33.1 Propagation using nonadiabatic couplings
8.33.2 Propagation using overlap matrices – Local diabatization
8.33.3 Propagation using overlap matrices – Norm-preserving interpolation
8.34 Evaluation of Time Derivative Couplings and Curvature Approximation
Chapter 1
Introduction
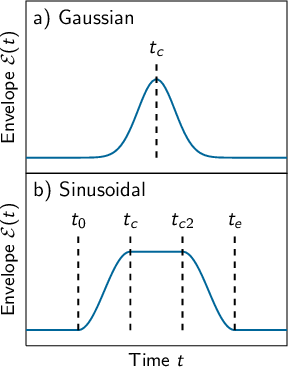
When a molecule is irradiated by light, a number of dynamical processes can take place, in which the molecule redistributes the energy among different electronic and vibrational degrees of freedom. Kasha’s rule [1] states that radiationless transfer from higher excited singlet states to the lowest-lying excited singlet state (S1) is faster than fluorescence (F). This radiationless transfer is called internal conversion (IC) and involves a changes between electronic states of the same multiplicity. If a transition occurs between electronic states of different spin, the process is called intersystem crossing (ISC). A typical ISC process is from a singlet to a triplet state, and once the lowest triplet is populated, phosphorescence (P) can take place. In figure 1.1, radiative (F and P) and radiationless (IC and ISC) processes are summarized in a so-called Jablonski diagram.
The non-radiative IC and ISC processes are fundamental concepts which play a decisive role in photochemistry and photobiology. IC processes are present in the excited-state dynamics of many organic and inorganic molecules, whose applications range from solar energy conversion to drug therapy. Even many, very small molecules, for example O2 and O3, SO2, NO2 and other nitrous oxides, show efficient IC, which has important consequences in atmospheric chemistry and the study of the environment and pollution. IC is also the first step of the biological process of visual perception, where the retinal moiety of rhodopsin absorbs a photon and non-radiatively performs a torsion around one of the double bonds, changing the conformation of the protein and inducing a neural signal. Similarly, protection of the human body from the influence of UV light is achieved through very efficient IC in DNA, proteins and melanins. Ultrafast IC to the electronic ground state allows quickly converting the excitation energy of the UV photons into nuclear kinetic energy, which is spread harmlessly as heat to the environment.
ISC processes are completely forbidden in the frame of the non-relativistic Schrödinger equation, but they become allowed when including spin-orbit couplings, a relativistic effect [2]. Spin-orbit coupling depends on the nuclear charge and becomes stronger for heavy atoms, therefore it is typically known as a “heavy atom” effect. However, it has been recently recognized that even for molecules with only first- and second-row atoms, ISC might be relevant and can be competitive in time scales with IC. A small selection of the growing number of molecules where efficient ISC in a sub-ps time scale has been predicted are SO2 [3,[4,[5], benzene [6], aromatic nitrocompounds [7] or DNA nucleobases and derivatives [8,[9,[10,[11,[12].
Theoretical simulations can greatly contribute to understand non-radiative processes by following the nuclear motion on the excited-state potential energy surfaces (PES) in real time. These simulations are called excited-state dynamics simulations.
Since the Born-Oppenheimer approximation is not applicable for this kind of dynamics, nonadiabatic effects need to be incorporated into the simulations.
The principal methodology to tackle excited-state dynamics simulations is to numerically integrate the time-dependent Schrödinger equation, which is usually called full quantum dynamics simulations (QD). Given accurate PESs, QD is able to match experimental accuracy. However, the need for the “a priori” knowledge of the full multi-dimensional PES renders this type of simulations quickly unfeasible for more than few degrees of freedom. Several alternative methodologies are possible to alleviate this problem. One of the most popular ones is to use surface hopping nonadiabatic dynamics.
Surface hopping was originally devised by Tully [13] and greatly improved later by the “fewest-switches criterion”[14] and it has been reviewed extensively since then, see e.g. [15,[16,[17,[18,[19].
In surface hopping, the motion of the excited-state wave packet is approximated by the motion of an ensemble of many independent, classical trajectories. Each trajectory is at every instant of time tied to one particular PES, and the nuclear motion is integrated using the gradient of this PES. However, nonadiabatic population transfer can lead to the switching of a trajectory from one PES to another PES. This switching (also called “hopping”, which is the origin of the name “surface hopping”) is based on a stochastic algorithm, taking into account the change of the electronic population from one time step to the next one.
The advantages of the surface hopping methodology and thus its popularity are well summarized in Ref. [15]:
- The method is conceptually simple, since it is based on classical mechanics. The nuclear propagation is based on Newton’s equations and can be performed in Cartesian coordinates, avoiding any problems with curved coordinate systems as in QD.
- For the propagation of the trajectories only local information of the PESs is needed. This avoids the calculation of the full, multi-dimensional PES in advance, which is the main bottleneck of QD methods. In surface hopping dynamics, all degrees of freedom can be included in the simulation. Additionally, all necessary quantities can be calculated on-demand, usually called “on-the-fly” in this context.
- The independent trajectories can be trivially parallelized.
The strongest of these points of course is the fact that all degrees of freedom can be included easily in the calculations, allowing to describe large systems.
One should note, however, that surface hopping methods in the standard formulation [13,[14]-due to the classical nature of the trajectories-do not allow to treat some purely quantum-mechanical effects like tunneling, (tunneling for selected degrees of freedom is possible [20]). Additionally, quantum coherence between the electronic states is usually described poorly, because of the independent-trajectory ansatz. This can be treated with some ad-hoc corrections, e.g., in [21].
In the original surface hopping method, only nonadiabatic couplings are considered, only allowing for population transfer between electronic states of the same multiplicity (IC).
The SHARC methodology is a generalization of standard surface hopping since it allows to include any type of coupling. Beyond nonadiabatic couplings (for IC), spin-orbit couplings (for ISC) or interactions of dipole moments with electric fields (to explicitly describe laser-induced processes) can be included.
A number of methodologies for surface hopping including one or the other type of potential couplings have been proposed in references [22,[23,[24,[25,[26,[27,[28], but SHARC can include all types of potential couplings on the same footing.
The SHARC methodology is an extension to standard surface hopping which allows to include these kinds of couplings. The central idea of SHARC is to obtain a fully diagonal Hamiltonian, which is adiabatic with respect to all couplings. The diagonal Hamiltonian is obtained by unitary transformation of the Hamiltonian including all couplings. Surface hopping is conducted on the transformed electronic states.
This has a number of advantages over the standard surface hopping methodology, where no diagonalization is performed:
- Potential couplings (like spin-orbit couplings and laser-dipole couplings) are usually delocalized. Surface hopping, however, rests on the assumption that the couplings are localized and hence surface hops only occur in the small region where the couplings are large. Within SHARC, by transforming away the potential couplings, additional terms of nonadiabatic (kinetic) couplings arise, which are localized.
- The potential couplings have an influence on the gradients acting on the nuclei. To a good approximation, within SHARC it is possible to include this influence in the dynamics.
- When including spin-orbit couplings for states of higher multiplicity, diagonalization solves the problem of rotational invariance of the multiplet components (see [26]).
The SHARC suite of programs is an implementation of the SHARC method. Besides the core dynamics code, it comes with a number of tools aiding in the setup, maintenance and analysis of the trajectories.
1.1 Capabilities
The main features of the SHARC suite are:
- Non-adiabatic dynamics based on the surface hopping methodology able to describe internal conversion and intersystem crossing with any number of states (singlets, doublets, triplets, or higher multiplicities).
- Algorithms for stable wave function propagation in the presence of very small or very large couplings.
- Inclusion of interactions with laser fields in the long-wavelength limit. The derivatives of the dipole moments can be included in strong-field applications.
- Propagation using either nonadiabatic couplings vectors 〈α|[(∂)/(∂R)]|β〉 or wave function overlaps 〈α(t0)|β(t)〉 (via the local diabatization procedure [21]).
- Gradients including the effects of spin-orbit couplings (with the approximation that the diabatic spin-orbit couplings are slowly varying).
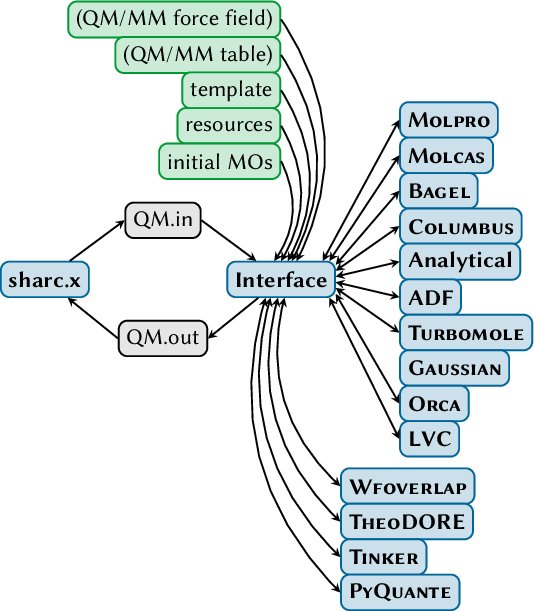
- Flexible interface to quantum chemistry programs. Existing interfaces to:
- MOLPRO 2010 and 2012: SA-CASSCF
- OPENMOLCAS 18.0: SA-CASSCF, SS-CASPT2, MS-CASPT2, SA-CASSCF+QM/MM
- COLUMBUS 7: SA-CASSCF, SA-RASSCF, MR-CISD
- ADF 2017+: TD-DFT, TD-DFT+QM/MM
- TURBOMOLE 7: ADC(2), CC2
- GAUSSIAN 09 and 16: TD-DFT
- ORCA 4.1: TD-DFT
- Interface for analytical potentials
- Interface for linear-vibronic coupling (LVC) models
- Energy-difference-based partial coupling approximation to speed up calculations [29].
- Energy-based decoherence correction [21] or augmented-FSSH decoherence correction [30].
- Calculation of Dyson norms for single-photon ionization spectra (for most interfaces) [31].
- On-the-fly wave function analysis with TheoDORE [32,[33,[34] (for some interfaces).
- Suite of auxiliary Python scripts for all steps of the setup procedure and for various analysis tasks.
- Comprehensive tutorial.
1.1.1 New features in SHARC Version 2.0
These features are new in SHARC Version 2.0 (2018):
- Dynamics program sharc.x:
- New methods: AFSSH for decoherence, GFSH for hopping probabilities, reflection after frustrated hop.
- Atom masking for size-extensive decoherence and rescaling.
- Improved wave function and U matrix phase tracking.
- Support for on-the-fly computation of Dyson norms and THEODORE descriptors.
- Option to gracefully stop trajectories after any time step.
- Fully integrated, efficient wave function overlap program wfoverlap.x
- Quantum chemistry interfaces:
- MOLPRO: overhauled, uses wfoverlap.x, gives consistent phase between CASSCF and CI wave functions, can do Dyson norms, parallelizes independent job parts.
- MOLCAS: overhauled, can do (MS)-CASPT2 (only numerical gradients), QM/MM, Cholesky decomposition, Dyson norms, parallelizes independent job parts, works with OPENMOLCAS version 18.
- COLUMBUS: overhauled, uses wfoverlap.x, can use DALTON integrals, can use MOLCAS orbitals, can do Dyson norms.
- ANALYTICAL: –
- TURBOMOLE: new interface, can do ADC(2) and CC2; has SOC (for ADC(2)), uses wfoverlap.x, works with THEODORE.
- ADF: new interface, can do TD-DFT; has SOC, uses wfoverlap.x, Dyson norms, has QM/MM, works with THEODORE.
- GAUSSIAN: new interface, can do TD-DFT; uses wfoverlap.x, has Dyson norms, works with THEODORE.
- LVC: new interface, can do (analytical) linear vibronic coupling models.
- Auxilliary scripts:
- wigner.py: elevated temperature sampling, LVC model setup.
- amber_to_initconds.py: new script, converts AMBER trajectories to SHARC initial conditions.
- sharctraj_to_initconds.py: new script, converts SHARC trajectories to SHARC initial conditions.
- spectrum.py: log-normal convolution, density of state spectra.
- data_extractor.x: new quantities to extract.
- diagnostics.py: new script, checks all trajectories prior to analysis.
- populations.py: new analysis modes.
- transition.py: new script, computes total number of hops in ensemble.
- make_fitscript.py: new script, prepares kinetic model fits to obtain time constants from populations.
- bootstrap.py: new script, calculates error estimates for time constants.
- trajana_essdyn.py: new script, performs essential dynamics analysis.
- trajana_nma.py: new script, performs normal mode analysis.
- data_collector.py: new script, performs generic data analysis (collecting, smoothing, convolution, integration).
- orca_External: new script, allows optimization with ORCA and SHARC.
- Several input generation helpers.
- Reworked tutorial using OPENMOLCAS (which is available at no cost).
1.1.2 New features in SHARC Version 2.1
These features are new in SHARC Version 2.1 (2019):
- Dynamics program sharc.x:
- New methods: Rescaling along gradient difference vector, forced hops to ground state.
- Output: Control of output step, writing to NetCDF format
- Dynamics program pysharc:
- Dynamics driver based on Python with C extension, allows to execute the routines of sharc.x directly within Python, which avoids file-based interface operations. Provides extremely efficient SHARC dynamics with LVC models.
- Data extraction:
- New options in data_extractor.x (e.g., populations according to [35]).
- New extractor for NetCDF files (data_extractor_NetCDF.x).
- Data converter (ASCII to NetCDF) (data_converter.x), useful for archiving.
- Quantum chemistry interfaces:
- MOLCAS: now works with OPENMOLCAS version 18 or MOLCAS 8.3 and 8.4.
- TURBOMOLE: now works with TURBOMOLE versions 7.1 to 7.4. Can now do QM/MM with TINKER.
- ORCA: new interface, can do TD-DFT; uses wfoverlap.x, has Dyson norms, works with THEODORE, can do QM/MM with TINKER.
- BAGEL: new interface, can do CASSCF, CASPT2, (X)MS-CASPT2 with analytical gradients and nonadiabatic couplings, has overlaps and Dyson norms from wfoverlap.x.
- ADF interface: updated for ADF2019 and newer, not backward compatible with older ADF versions.
- Auxilliary scripts:
- sharcvars.sh, sharcvars.csh: can be sourced to automatically set all relevant environment variables for sharc.x, pysharc, and programs using NetCDF.
- make_fit.py: new script, more flexible, efficient, and integrated script for kinetic model fitting. Replaces the scripts make_fitscript.py and bootstrap.py.
- setup_LVCparam.py and create_LVCparam.py: new setup scripts to automatically generate LVC models from quantum chemistry calculations (also without nonadiabatic coupling vectors).
1.1.3 New features in SHARC Version 2.1.1
These features are new in SHARC Version 2.1.1 (2021):
- Dynamics program sharc.x:
- RATTLE algorithm for constraint bond lengths
- Keyword for restart control
- Bug fixes
- SchNarc for machine learning properties is available at https://github.com/schnarc/SchNarc
1.1.4 New features in SHARC Version 3.0
These features are new in SHARC Version 3.0 (2023):
- Dynamics program sharc.x:
- CSDM: coherent switching with decay of mixing
- SCDM: self-consistent decay of mixing
- tSE: time-derivative semiclassical Ehrenfest
- tCSDM: time-derivative coherent switching with decay of mixing
- \upkappaSE: curvature-driven semiclassical Ehrenfest
- \upkappaCSDM: curvature-driven coherent switching with decay of mixing
- \upkappaTSH: curvature-driven trajectory surface hooping
- Time-derivative-matrix (TDM) gradient correction scheme
- TSH-FSTU: trajectory surface hopping with time uncertainty
- Projection operator that conserves angular momentum and center of mass motion
- New options for momentum adjustment vector and velocity reflection vector in TSH
- Adaptive time step velocity Verlet algorithm
- Bug fixes
- Interfaces and scripts *.py:
- Switch to Python 3
- State selected initial conditions: state_selected.py
- MOLCAS interface SHARC_MOLCAS.py:
- MS-PDFT:
- XMS-PDFT
- CMS-PDFT
1.2 References
The following references should be cited when using the SHARC suite:
Details can be found in the following references:
The theoretical background of SHARC is described in Refs. [38,[39,[40,[41,[42,[36,[43].
Applications of the SHARC code can be found in Refs. [9,[11,[44,[4,[45,[46,[47,[48,[49,[50,[51,[52,[53,[54,[55,[56,[57,[58,[59,[60,[61,[62,[63,[64,[65,[66,[67,[68,[69,[70].
Other features implemented in the SHARC suite are described in the following references:
- Energy-based decoherence correction: [21].
- Augmented-FSSH decoherence correction: [30].
- Global flux SH: [71].
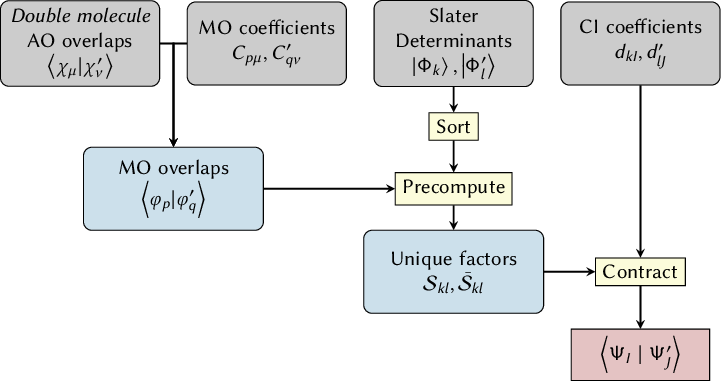
- Local diabatization and wave function overlap calculation: [72,[73,[74].
- Sampling of initial conditions from a quantum-mechanical harmonic Wigner distribution: [75,[76,[77].
- Excited state selection for initial condition generation: [78].
- Calculation of ring puckering parameters and their classification: [79,[80].
- Normal mode analysis [81,[82] and essential dynamics analysis: [83,[82].
- Bootstrapping for error estimation: [84].
- Crossing point optimization: [85,[86]
- Computation of ionization spectra: [31,[87].
- Wave function comparison with overlaps: [88].
- Dynamics with linear vibronic coupling models: [89].
- Computation of electronic populations: [35].
- Dynamics with neural network potentials and other machine learning properties: [90]
- Coherent switching with decay of mixing: [91,[92]
- Time derivative algorithms tSE and tCSDM: [93]
- Curvature driven algorithms \upkappaSE, \upkappaTSH, and \upkappaCSDM: [94]
- Projection operator conserves angular momentum and center of mass motion: [95]
- Time-derivative-matrix gradient correction scheme: [96]
- Trajectory surface hopping with time uncertainty: [97,[98]
The quantum chemistry programs to which interfaces with SHARC exist are described in the following sources:
- MOLPRO: [99,[100],
- MOLCAS: [101,[102,[103,[104],
- COLUMBUS: [105,[106,[107,[108],
- ADF: [109],
- TURBOMOLE: [110],
- GAUSSIAN: [111,[112],
- ORCA: [113],
- BAGEL: [114].
Others:
1.3 Authors
The SHARC suite has been developed by
(listed alphabetically):
Andrew Atkins,
Davide Avagliano,
Sandra Gómez,
Leticia González,
Jesús González-Vázquez,
Moritz Heindl,
Lea M. Ibele,
Simon Kropf,
Sebastian Mai,
Philipp Marquetand,
Maximilian F. S. J. Menger,
Markus Oppel,
Felix Plasser,
Severin Polonius,
Martin Richter,
Matthias Ruckenbauer,
Yinan Shu,
Ignacio Sóla,
Donald G. Truhlar,
Linyao Zhang, and
Patrick Zobel.
1.4 Suggestions and Bug Reports
Bug reports and suggestions for possible features can be submitted to sharc@univie.ac.at.
1.5 Notation in this Manual
Names of programs
The SHARC suite consists of Fortran90 programs as well as Python and Shell scripts. The executable Fortran90 programs are denoted by the extension .x, the Python scripts have the extension .py and the Shell scripts .sh. Within this manual, all program names are given in bold monospaced font.
Chapter 2
Installation
2.1 How To Obtain
SHARC can be obtained from the SHARC homepage www.sharc-md.org. In the Download section, follow the link to GITHUB to clone or download the latest SHARC release version.
Note that you accept the Terms of Use given in the following section when you download SHARC.
2.2 Terms of Use
SHARC Program Suite
Copyright 2019, University of Vienna
SHARC is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
SHARC is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
A copy of the GNU General Public License is given below.
It is also available at www.gnu.org/licenses/.
1. Preamble
The GNU General Public License is a free, copyleft license for
software and other kinds of works.
The licenses for most software and other practical works are designed
to take away your freedom to share and change the works. By contrast,
the GNU General Public License is intended to guarantee your freedom to
share and change all versions of a program-to make sure it remains free
software for all its users. We, the Free Software Foundation, use the
GNU General Public License for most of our software; it applies also to
any other work released this way by its authors. You can apply it to
your programs, too.
When we speak of free software, we are referring to freedom, not
price. Our General Public Licenses are designed to make sure that you
have the freedom to distribute copies of free software (and charge for
them if you wish), that you receive source code or can get it if you
want it, that you can change the software or use pieces of it in new
free programs, and that you know you can do these things.
To protect your rights, we need to prevent others from denying you
these rights or asking you to surrender the rights. Therefore, you have
certain responsibilities if you distribute copies of the software, or if
you modify it: responsibilities to respect the freedom of others.
For example, if you distribute copies of such a program, whether
gratis or for a fee, you must pass on to the recipients the same
freedoms that you received. You must make sure that they, too, receive
or can get the source code. And you must show them these terms so they
know their rights.
Developers that use the GNU GPL protect your rights with two steps:
(1) assert copyright on the software, and (2) offer you this License
giving you legal permission to copy, distribute and/or modify it.
For the developers’ and authors’ protection, the GPL clearly explains
that there is no warranty for this free software. For both users’ and
authors’ sake, the GPL requires that modified versions be marked as
changed, so that their problems will not be attributed erroneously to
authors of previous versions.
Some devices are designed to deny users access to install or run
modified versions of the software inside them, although the manufacturer
can do so. This is fundamentally incompatible with the aim of
protecting users’ freedom to change the software. The systematic
pattern of such abuse occurs in the area of products for individuals to
use, which is precisely where it is most unacceptable. Therefore, we
have designed this version of the GPL to prohibit the practice for those
products. If such problems arise substantially in other domains, we
stand ready to extend this provision to those domains in future versions
of the GPL, as needed to protect the freedom of users.
Finally, every program is threatened constantly by software patents.
States should not allow patents to restrict development and use of
software on general-purpose computers, but in those that do, we wish to
avoid the special danger that patents applied to a free program could
make it effectively proprietary. To prevent this, the GPL assures that
patents cannot be used to render the program non-free.
The precise terms and conditions for copying, distribution and
modification follow.
2. Terms and Conditions
- Definitions.
“This License” refers to version 3 of the GNU General Public License.
“Copyright” also means copyright-like laws that apply to other kinds of
works, such as semiconductor masks.“The Program” refers to any copyrightable work licensed under this
License. Each licensee is addressed as “you”. “Licensees” and
“recipients” may be individuals or organizations.To “modify” a work means to copy from or adapt all or part of the work
in a fashion requiring copyright permission, other than the making of an
exact copy. The resulting work is called a “modified version” of the
earlier work or a work “based on” the earlier work.A “covered work” means either the unmodified Program or a work based
on the Program.To “propagate” a work means to do anything with it that, without
permission, would make you directly or secondarily liable for
infringement under applicable copyright law, except executing it on a
computer or modifying a private copy. Propagation includes copying,
distribution (with or without modification), making available to the
public, and in some countries other activities as well.To “convey” a work means any kind of propagation that enables other
parties to make or receive copies. Mere interaction with a user through
a computer network, with no transfer of a copy, is not conveying.An interactive user interface displays “Appropriate Legal Notices”
to the extent that it includes a convenient and prominently visible
feature that (1) displays an appropriate copyright notice, and (2)
tells the user that there is no warranty for the work (except to the
extent that warranties are provided), that licensees may convey the
work under this License, and how to view a copy of this License. If
the interface presents a list of user commands or options, such as a
menu, a prominent item in the list meets this criterion. - Source Code.
The “source code” for a work means the preferred form of the work
for making modifications to it. “Object code” means any non-source
form of a work.A “Standard Interface” means an interface that either is an official
standard defined by a recognized standards body, or, in the case of
interfaces specified for a particular programming language, one that
is widely used among developers working in that language.The “System Libraries” of an executable work include anything, other
than the work as a whole, that (a) is included in the normal form of
packaging a Major Component, but which is not part of that Major
Component, and (b) serves only to enable use of the work with that
Major Component, or to implement a Standard Interface for which an
implementation is available to the public in source code form. A
“Major Component”, in this context, means a major essential component
(kernel, window system, and so on) of the specific operating system
(if any) on which the executable work runs, or a compiler used to
produce the work, or an object code interpreter used to run it.The “Corresponding Source” for a work in object code form means all
the source code needed to generate, install, and (for an executable
work) run the object code and to modify the work, including scripts to
control those activities. However, it does not include the work’s
System Libraries, or general-purpose tools or generally available free
programs which are used unmodified in performing those activities but
which are not part of the work. For example, Corresponding Source
includes interface definition files associated with source files for
the work, and the source code for shared libraries and dynamically
linked subprograms that the work is specifically designed to require,
such as by intimate data communication or control flow between those
subprograms and other parts of the work.The Corresponding Source need not include anything that users
can regenerate automatically from other parts of the Corresponding
Source.The Corresponding Source for a work in source code form is that
same work. - Basic Permissions.
All rights granted under this License are granted for the term of
copyright on the Program, and are irrevocable provided the stated
conditions are met. This License explicitly affirms your unlimited
permission to run the unmodified Program. The output from running a
covered work is covered by this License only if the output, given its
content, constitutes a covered work. This License acknowledges your
rights of fair use or other equivalent, as provided by copyright law.You may make, run and propagate covered works that you do not
convey, without conditions so long as your license otherwise remains
in force. You may convey covered works to others for the sole purpose
of having them make modifications exclusively for you, or provide you
with facilities for running those works, provided that you comply with
the terms of this License in conveying all material for which you do
not control copyright. Those thus making or running the covered works
for you must do so exclusively on your behalf, under your direction
and control, on terms that prohibit them from making any copies of
your copyrighted material outside their relationship with you.Conveying under any other circumstances is permitted solely under
the conditions stated below. Sublicensing is not allowed; section 10
makes it unnecessary. - Protecting Users’ Legal Rights From Anti-Circumvention Law.
No covered work shall be deemed part of an effective technological
measure under any applicable law fulfilling obligations under article
11 of the WIPO copyright treaty adopted on 20 December 1996, or
similar laws prohibiting or restricting circumvention of such
measures.When you convey a covered work, you waive any legal power to forbid
circumvention of technological measures to the extent such circumvention
is effected by exercising rights under this License with respect to
the covered work, and you disclaim any intention to limit operation or
modification of the work as a means of enforcing, against the work’s
users, your or third parties’ legal rights to forbid circumvention of
technological measures. - Conveying Verbatim Copies.
You may convey verbatim copies of the Program’s source code as you
receive it, in any medium, provided that you conspicuously and
appropriately publish on each copy an appropriate copyright notice;
keep intact all notices stating that this License and any
non-permissive terms added in accord with section 7 apply to the code;
keep intact all notices of the absence of any warranty; and give all
recipients a copy of this License along with the Program.You may charge any price or no price for each copy that you convey,
and you may offer support or warranty protection for a fee. - Conveying Modified Source Versions.
You may convey a work based on the Program, or the modifications to
produce it from the Program, in the form of source code under the
terms of section 4, provided that you also meet all of these conditions:- The work must carry prominent notices stating that you modified
it, and giving a relevant date. - The work must carry prominent notices stating that it is
released under this License and any conditions added under section
7. This requirement modifies the requirement in section 4 to
“keep intact all notices”. - You must license the entire work, as a whole, under this
License to anyone who comes into possession of a copy. This
License will therefore apply, along with any applicable section 7
additional terms, to the whole of the work, and all its parts,
regardless of how they are packaged. This License gives no
permission to license the work in any other way, but it does not
invalidate such permission if you have separately received it. - If the work has interactive user interfaces, each must display
Appropriate Legal Notices; however, if the Program has interactive
interfaces that do not display Appropriate Legal Notices, your
work need not make them do so.
A compilation of a covered work with other separate and independent
works, which are not by their nature extensions of the covered work,
and which are not combined with it such as to form a larger program,
in or on a volume of a storage or distribution medium, is called an
“aggregate” if the compilation and its resulting copyright are not
used to limit the access or legal rights of the compilation’s users
beyond what the individual works permit. Inclusion of a covered work
in an aggregate does not cause this License to apply to the other
parts of the aggregate. - The work must carry prominent notices stating that you modified
- Conveying Non-Source Forms.
You may convey a covered work in object code form under the terms
of sections 4 and 5, provided that you also convey the
machine-readable Corresponding Source under the terms of this License,
in one of these ways:- Convey the object code in, or embodied in, a physical product
(including a physical distribution medium), accompanied by the
Corresponding Source fixed on a durable physical medium
customarily used for software interchange. - Convey the object code in, or embodied in, a physical product
(including a physical distribution medium), accompanied by a
written offer, valid for at least three years and valid for as
long as you offer spare parts or customer support for that product
model, to give anyone who possesses the object code either (1) a
copy of the Corresponding Source for all the software in the
product that is covered by this License, on a durable physical
medium customarily used for software interchange, for a price no
more than your reasonable cost of physically performing this
conveying of source, or (2) access to copy the
Corresponding Source from a network server at no charge. - Convey individual copies of the object code with a copy of the
written offer to provide the Corresponding Source. This
alternative is allowed only occasionally and noncommercially, and
only if you received the object code with such an offer, in accord
with subsection 6b. - Convey the object code by offering access from a designated
place (gratis or for a charge), and offer equivalent access to the
Corresponding Source in the same way through the same place at no
further charge. You need not require recipients to copy the
Corresponding Source along with the object code. If the place to
copy the object code is a network server, the Corresponding Source
may be on a different server (operated by you or a third party)
that supports equivalent copying facilities, provided you maintain
clear directions next to the object code saying where to find the
Corresponding Source. Regardless of what server hosts the
Corresponding Source, you remain obligated to ensure that it is
available for as long as needed to satisfy these requirements. - Convey the object code using peer-to-peer transmission, provided
you inform other peers where the object code and Corresponding
Source of the work are being offered to the general public at no
charge under subsection 6d.
A separable portion of the object code, whose source code is excluded
from the Corresponding Source as a System Library, need not be
included in conveying the object code work.A “User Product” is either (1) a “consumer product”, which means any
tangible personal property which is normally used for personal, family,
or household purposes, or (2) anything designed or sold for incorporation
into a dwelling. In determining whether a product is a consumer product,
doubtful cases shall be resolved in favor of coverage. For a particular
product received by a particular user, “normally used” refers to a
typical or common use of that class of product, regardless of the status
of the particular user or of the way in which the particular user
actually uses, or expects or is expected to use, the product. A product
is a consumer product regardless of whether the product has substantial
commercial, industrial or non-consumer uses, unless such uses represent
the only significant mode of use of the product.“Installation Information” for a User Product means any methods,
procedures, authorization keys, or other information required to install
and execute modified versions of a covered work in that User Product from
a modified version of its Corresponding Source. The information must
suffice to ensure that the continued functioning of the modified object
code is in no case prevented or interfered with solely because
modification has been made.If you convey an object code work under this section in, or with, or
specifically for use in, a User Product, and the conveying occurs as
part of a transaction in which the right of possession and use of the
User Product is transferred to the recipient in perpetuity or for a
fixed term (regardless of how the transaction is characterized), the
Corresponding Source conveyed under this section must be accompanied
by the Installation Information. But this requirement does not apply
if neither you nor any third party retains the ability to install
modified object code on the User Product (for example, the work has
been installed in ROM).The requirement to provide Installation Information does not include a
requirement to continue to provide support service, warranty, or updates
for a work that has been modified or installed by the recipient, or for
the User Product in which it has been modified or installed. Access to a
network may be denied when the modification itself materially and
adversely affects the operation of the network or violates the rules and
protocols for communication across the network.Corresponding Source conveyed, and Installation Information provided,
in accord with this section must be in a format that is publicly
documented (and with an implementation available to the public in
source code form), and must require no special password or key for
unpacking, reading or copying. - Convey the object code in, or embodied in, a physical product
- Additional Terms.
“Additional permissions” are terms that supplement the terms of this
License by making exceptions from one or more of its conditions.
Additional permissions that are applicable to the entire Program shall
be treated as though they were included in this License, to the extent
that they are valid under applicable law. If additional permissions
apply only to part of the Program, that part may be used separately
under those permissions, but the entire Program remains governed by
this License without regard to the additional permissions.When you convey a copy of a covered work, you may at your option
remove any additional permissions from that copy, or from any part of
it. (Additional permissions may be written to require their own
removal in certain cases when you modify the work.) You may place
additional permissions on material, added by you to a covered work,
for which you have or can give appropriate copyright permission.Notwithstanding any other provision of this License, for material you
add to a covered work, you may (if authorized by the copyright holders of
that material) supplement the terms of this License with terms:- Disclaiming warranty or limiting liability differently from the
terms of sections 15 and 16 of this License; or - Requiring preservation of specified reasonable legal notices or
author attributions in that material or in the Appropriate Legal
Notices displayed by works containing it; or - Prohibiting misrepresentation of the origin of that material, or
requiring that modified versions of such material be marked in
reasonable ways as different from the original version; or - Limiting the use for publicity purposes of names of licensors or
authors of the material; or - Declining to grant rights under trademark law for use of some
trade names, trademarks, or service marks; or - Requiring indemnification of licensors and authors of that
material by anyone who conveys the material (or modified versions of
it) with contractual assumptions of liability to the recipient, for
any liability that these contractual assumptions directly impose on
those licensors and authors.
All other non-permissive additional terms are considered “further
restrictions” within the meaning of section 10. If the Program as you
received it, or any part of it, contains a notice stating that it is
governed by this License along with a term that is a further
restriction, you may remove that term. If a license document contains
a further restriction but permits relicensing or conveying under this
License, you may add to a covered work material governed by the terms
of that license document, provided that the further restriction does
not survive such relicensing or conveying.If you add terms to a covered work in accord with this section, you
must place, in the relevant source files, a statement of the
additional terms that apply to those files, or a notice indicating
where to find the applicable terms.Additional terms, permissive or non-permissive, may be stated in the
form of a separately written license, or stated as exceptions;
the above requirements apply either way. - Disclaiming warranty or limiting liability differently from the
- Termination.
You may not propagate or modify a covered work except as expressly
provided under this License. Any attempt otherwise to propagate or
modify it is void, and will automatically terminate your rights under
this License (including any patent licenses granted under the third
paragraph of section 11).However, if you cease all violation of this License, then your
license from a particular copyright holder is reinstated (a)
provisionally, unless and until the copyright holder explicitly and
finally terminates your license, and (b) permanently, if the copyright
holder fails to notify you of the violation by some reasonable means
prior to 60 days after the cessation.Moreover, your license from a particular copyright holder is
reinstated permanently if the copyright holder notifies you of the
violation by some reasonable means, this is the first time you have
received notice of violation of this License (for any work) from that
copyright holder, and you cure the violation prior to 30 days after
your receipt of the notice.Termination of your rights under this section does not terminate the
licenses of parties who have received copies or rights from you under
this License. If your rights have been terminated and not permanently
reinstated, you do not qualify to receive new licenses for the same
material under section 10. - Acceptance Not Required for Having Copies.
You are not required to accept this License in order to receive or
run a copy of the Program. Ancillary propagation of a covered work
occurring solely as a consequence of using peer-to-peer transmission
to receive a copy likewise does not require acceptance. However,
nothing other than this License grants you permission to propagate or
modify any covered work. These actions infringe copyright if you do
not accept this License. Therefore, by modifying or propagating a
covered work, you indicate your acceptance of this License to do so. - Automatic Licensing of Downstream Recipients.
Each time you convey a covered work, the recipient automatically
receives a license from the original licensors, to run, modify and
propagate that work, subject to this License. You are not responsible
for enforcing compliance by third parties with this License.An “entity transaction” is a transaction transferring control of an
organization, or substantially all assets of one, or subdividing an
organization, or merging organizations. If propagation of a covered
work results from an entity transaction, each party to that
transaction who receives a copy of the work also receives whatever
licenses to the work the party’s predecessor in interest had or could
give under the previous paragraph, plus a right to possession of the
Corresponding Source of the work from the predecessor in interest, if
the predecessor has it or can get it with reasonable efforts.You may not impose any further restrictions on the exercise of the
rights granted or affirmed under this License. For example, you may
not impose a license fee, royalty, or other charge for exercise of
rights granted under this License, and you may not initiate litigation
(including a cross-claim or counterclaim in a lawsuit) alleging that
any patent claim is infringed by making, using, selling, offering for
sale, or importing the Program or any portion of it. - Patents.
A “contributor” is a copyright holder who authorizes use under this
License of the Program or a work on which the Program is based. The
work thus licensed is called the contributor’s “contributor version”.A contributor’s “essential patent claims” are all patent claims
owned or controlled by the contributor, whether already acquired or
hereafter acquired, that would be infringed by some manner, permitted
by this License, of making, using, or selling its contributor version,
but do not include claims that would be infringed only as a
consequence of further modification of the contributor version. For
purposes of this definition, “control” includes the right to grant
patent sublicenses in a manner consistent with the requirements of
this License.Each contributor grants you a non-exclusive, worldwide, royalty-free
patent license under the contributor’s essential patent claims, to
make, use, sell, offer for sale, import and otherwise run, modify and
propagate the contents of its contributor version.In the following three paragraphs, a “patent license” is any express
agreement or commitment, however denominated, not to enforce a patent
(such as an express permission to practice a patent or covenant not to
sue for patent infringement). To “grant” such a patent license to a
party means to make such an agreement or commitment not to enforce a
patent against the party.If you convey a covered work, knowingly relying on a patent license,
and the Corresponding Source of the work is not available for anyone
to copy, free of charge and under the terms of this License, through a
publicly available network server or other readily accessible means,
then you must either (1) cause the Corresponding Source to be so
available, or (2) arrange to deprive yourself of the benefit of the
patent license for this particular work, or (3) arrange, in a manner
consistent with the requirements of this License, to extend the patent
license to downstream recipients. “Knowingly relying” means you have
actual knowledge that, but for the patent license, your conveying the
covered work in a country, or your recipient’s use of the covered work
in a country, would infringe one or more identifiable patents in that
country that you have reason to believe are valid.If, pursuant to or in connection with a single transaction or
arrangement, you convey, or propagate by procuring conveyance of, a
covered work, and grant a patent license to some of the parties
receiving the covered work authorizing them to use, propagate, modify
or convey a specific copy of the covered work, then the patent license
you grant is automatically extended to all recipients of the covered
work and works based on it.A patent license is “discriminatory” if it does not include within
the scope of its coverage, prohibits the exercise of, or is
conditioned on the non-exercise of one or more of the rights that are
specifically granted under this License. You may not convey a covered
work if you are a party to an arrangement with a third party that is
in the business of distributing software, under which you make payment
to the third party based on the extent of your activity of conveying
the work, and under which the third party grants, to any of the
parties who would receive the covered work from you, a discriminatory
patent license (a) in connection with copies of the covered work
conveyed by you (or copies made from those copies), or (b) primarily
for and in connection with specific products or compilations that
contain the covered work, unless you entered into that arrangement,
or that patent license was granted, prior to 28 March 2007.Nothing in this License shall be construed as excluding or limiting
any implied license or other defenses to infringement that may
otherwise be available to you under applicable patent law. - No Surrender of Others’ Freedom.
If conditions are imposed on you (whether by court order, agreement or
otherwise) that contradict the conditions of this License, they do not
excuse you from the conditions of this License. If you cannot convey a
covered work so as to satisfy simultaneously your obligations under this
License and any other pertinent obligations, then as a consequence you may
not convey it at all. For example, if you agree to terms that obligate you
to collect a royalty for further conveying from those to whom you convey
the Program, the only way you could satisfy both those terms and this
License would be to refrain entirely from conveying the Program. - Use with the GNU Affero General Public License.
Notwithstanding any other provision of this License, you have
permission to link or combine any covered work with a work licensed
under version 3 of the GNU Affero General Public License into a single
combined work, and to convey the resulting work. The terms of this
License will continue to apply to the part which is the covered work,
but the special requirements of the GNU Affero General Public License,
section 13, concerning interaction through a network will apply to the
combination as such. - Revised Versions of this License.
The Free Software Foundation may publish revised and/or new versions of
the GNU General Public License from time to time. Such new versions will
be similar in spirit to the present version, but may differ in detail to
address new problems or concerns.Each version is given a distinguishing version number. If the
Program specifies that a certain numbered version of the GNU General
Public License “or any later version” applies to it, you have the
option of following the terms and conditions either of that numbered
version or of any later version published by the Free Software
Foundation. If the Program does not specify a version number of the
GNU General Public License, you may choose any version ever published
by the Free Software Foundation.If the Program specifies that a proxy can decide which future
versions of the GNU General Public License can be used, that proxy’s
public statement of acceptance of a version permanently authorizes you
to choose that version for the Program.Later license versions may give you additional or different
permissions. However, no additional obligations are imposed on any
author or copyright holder as a result of your choosing to follow a
later version. - Disclaimer of Warranty.
THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PERMITTED BY
APPLICABLE LAW. EXCEPT WHEN OTHERWISE STATED IN WRITING THE
COPYRIGHT HOLDERS AND/OR OTHER PARTIES PROVIDE THE PROGRAM “AS IS”
WITHOUT WARRANTY OF ANY KIND, EITHER EXPRESSED OR IMPLIED,
INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF
MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE. THE ENTIRE
RISK AS TO THE QUALITY AND PERFORMANCE OF THE PROGRAM IS WITH YOU.
SHOULD THE PROGRAM PROVE DEFECTIVE, YOU ASSUME THE COST OF ALL
NECESSARY SERVICING, REPAIR OR CORRECTION. - Limitation of Liability.
IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN
WRITING WILL ANY COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MODIFIES
AND/OR CONVEYS THE PROGRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR
DAMAGES, INCLUDING ANY GENERAL, SPECIAL, INCIDENTAL OR CONSEQUENTIAL
DAMAGES ARISING OUT OF THE USE OR INABILITY TO USE THE PROGRAM
(INCLUDING BUT NOT LIMITED TO LOSS OF DATA OR DATA BEING RENDERED
INACCURATE OR LOSSES SUSTAINED BY YOU OR THIRD PARTIES OR A FAILURE
OF THE PROGRAM TO OPERATE WITH ANY OTHER PROGRAMS), EVEN IF SUCH
HOLDER OR OTHER PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH
DAMAGES. - Interpretation of Sections 15 and 16.
If the disclaimer of warranty and limitation of liability provided
above cannot be given local legal effect according to their terms,
reviewing courts shall apply local law that most closely approximates
an absolute waiver of all civil liability in connection with the
Program, unless a warranty or assumption of liability accompanies a
copy of the Program in return for a fee.
2.3 Installation
In order to install and run SHARC under Linux (Windows and OS X are currently not supported), you need the following:
- A Fortran90 compiler (This release is tested against GNU Fortran 8.5.0 and Intel Fortran 2021.8.0).
- The BLAS, LAPACK and FFTW3 libraries.
- Python 3 (This release is tested against Python 3.10).
- make.
- git.
- [Anaconda with several libraries (hdf5, hdf5_hl, netcdf, mfhdf, df, jpeg, gcc) for the pysharc and NetCDF functionalities.]
Extracting
The source code of the SHARC suite is distributed via github. In order to install it, first clone the repository in a suitable directory (where a directory called sharc will be automatically created):
git clone https://github.com/sharc-md/sharc.git
As mentioned above, this should create a new directory called sharc/ which contains all the necessary subdirectories and files.
In figure 2.1 the directory structure of the complete SHARC directory is shown.
Compiling and installing (without pysharc)
To compile the Fortran90 programs of the SHARC suite, go to the source/ directory.
cd source/
and edit the Makefile by adjusting the variables in the top part.
If you only want to install regular SHARC (no pysharc or NetCDF), set USE_PYSHARC to false.
Then, inside source/ issuing the command:
make
will compile the source and create all the binaries.
make install
will additionally copy the binary files into the sharc/bin/ directory of the
SHARC distribution, which already contains all the python scripts which
come with SHARC.
Compiling and installing (with pysharc)
If you intend to perform computations with pysharc (with LVC models) or with NetCDF functionality, you need to set USE_PYSHARC to true in source/Makefile.
Note that currently, some new options (adaptive time steps, time uncertainty hopping, decay of mixing decoherence, and Ehrenfest dynamics).
In order to compile with pysharc, it is necessary to first create a suitable Python installation through the Anaconda distribution.
A working minimal environment can be created with:
conda create -n pysharc_3.0 -c conda-forge python=3.9 numpy scipy h5py six matplotlib
python-dateutil pyyaml pyparsing kiwisolver cycler netcdf4 hdf5 h5utils gfortran_linux-64
Subsequently, the environment has to be activated with
conda activate pysharc_3.0
before one can proceed with the installation of pysharc.
Due to a number of dependencies, compiling with pysharc is slightly more complicated than without.
The simplest way to compile both pysharc and the regular executables together is to
- run make install in pysharc/, then
- run make install in source/.
Alternatively, you might want to compile the regular executables without pysharc or NetCDF, and then compile pysharc.
To do this:
- set USE_PYSHARC to false,
- run make install in source/,
- run make clean in source/,
- set USE_PYSHARC to true,
- run make install in pysharc/.
Environment setup
In order to use the SHARC suite, you have to set some environment variables. The recommended approach is to source either of the sharcvars files (generated by make) that are located in the bin/ directory. For example, if you have cloned SHARC into your home directory, just use:
source ~/sharc/bin/sharcvars.sh (for bourne shell users)
or
source ~/sharc/bin/sharcvars.csh (for c-shell type users)
Note that it may be convenient to put this line into your shell’s login
scripts.
The afore-mentioned procedure works from SHARC 2.1 on and also for later versions. For older versions, set the environment variable
$SHARC to the bin/ directory of the SHARC installation.
This ensures that all programs of the SHARC suite find the other executables and all calls are successful.
For example, if you have unpacked SHARC into your home directory, just set:
export SHARC=~/sharc/bin (for bourne shell users)
or
setenv SHARC $HOME/sharc/bin (for c-shell type users)
2.3.1 WFOVERLAP Program
The SHARC package contains as a submodule the program WFOVERLAP, which is necessary for many functionalities of SHARC.
In order to install and test this program, see section 6.13.
2.3.2 Libraries
SHARC requires the BLAS, LAPACK and FFTW3 libraries. During the installation, it might be necessary to alter the LDFLAGS string in the Makefile, depending on where the relevant libraries are located on your system. In this way, it is for example possible to use vendor-provided libraries like the Intel MKL. For more details see the INSTALL file which is included in the SHARC distribution.
As specified above, users of pysharc and the NetCDF functions will need additional libraries, e.g., obtained through ANACONDA:
conda create -n pysharc_3.0 -c conda-forge python=3.9 numpy scipy h5py six matplotlib
python-dateutil pyyaml pyparsing kiwisolver cycler netcdf4 hdf5 h5utils gfortran_linux-64
2.3.3 Test Suite
| Keyword | Description |
| $ADF | Points to the main directory of the ADF installation, which contains the file adfrc.sh and subdirectory bin/. |
| $BAGEL | Points to the main directory of the BAGEL installation, which contains subdirectories bin/ and lib/. |
| $COLUMBUS | Points to the directory containing the COLUMBUS executables, e.g., runls. |
| $GAUSSIAN | Points to the main directory of the GAUSSIAN installation, which contains the GAUSSIAN executables (e.g., g09/g16 or l9999.exe). |
| $MOLCAS | Points to the main directory of the OPENMOLCAS installation, containing molcas.rte and directories basis_library/ and bin/. |
| $MOLPRO | Points to the bin/ directory of the MOLPRO installation, which contains the molpro.exe file. |
| $TURBOMOLE | Points to the main directory of the TURBOMOLE installation, which contains subdirectories like basen/, bin/, or scripts/. |
| $ORCA | Points to the directory containing the ORCA executables, e.g., orca, orca_gtoint, or orca_fragovl. |
| $THEODORE | Points to the main directory of the THEODORE installation. $THEODORE/bin/ should contain analyze_tden.py. |
| $TINKER | Points to the main directory of a MOLCAS-modified TINKER installation. $TINKER/bin should contain tkr2qm_s). |
| $PYQUANTE | Points to the main directory of PYQUANTE, containing the PyQuante/ subdirectory that can be imported by Python as a module. |
| $molcas | Should point to the same location as $MOLCAS, or another MOLCAS installation. Note that $molcas is only used by some COLUMBUS test jobs. Also note that $molcas does not need to point to the MOLCAS installation interfaced to COLUMBUS. |
| $orca | Should point to the same location as $ORCA, or another ORCA installation. Note that $orca is only used by some tests where ORCA is used as helper program (e.g., for setup_orca_opt.py or spin-orbit calculations with SHARC_RICC2.py). |
After the installation, it is advisable to first execute the test suite of SHARC, which will test the fundamental functionality of SHARC.
Change to an empty directory and execute
$SHARC/tests.py
The interactive script will first verify the Python installation (no message will appear if the Python installation is fine).
Subsequently, the script prompts the user to enter which tests should be executed.
The script will also ask for a number of environment variables, which are listed in Table 2.1.
There is at least one test for each of the auxiliary scripts and interfaces.
Tests whose names start with scripts_ test the functionality of the auxiliary programs in the SHARC suite.
Tests whose names start with ADF_, Analytical_, COLUMBUS_, GAUSSIAN_, LVC_, MOLCAS_ MOLPRO_, or TURBOMOLE_ run short trajectories, testing whether the main dynamics code, the interfaces, the quantum chemistry programs, and auxiliary programs ( THEODORE, WFOVERLAP, ORCA, TINKER) work together correctly.
If the installation was successful and Python is installed correctly, Analytical_overlap, LVC_overlap, and most tests named scripts_<NAME> should execute without error.
The test calculations involving the quantum chemistry programs can be used to check that SHARC can correctly call these programs and that they are installed correctly.
If any of the tests show differences between output and reference output, it is advisable to check the respective files (i.e., compare $SHARC/../tests/RESULTS/<job>/ to ./RUNNING_TESTS/<job>/). Note that small differences (different sign of values or small numerical deviations) in the output can already occur when using a different version of the quantum chemistry programs, different compilers, different libraries, or different parallization schemes.
It should be noted that along trajectories, these small changes can add up to notably influence the trajectories, but across the ensemble these small changes will likely cancel out.
2.3.4 Additional Programs
For full functionality of the SHARC suite, several additional programs are recommended (all of these programs are currently freely available, except for AMBER):
- The Python package NUMPY.Optimally, within your Python installation the NUMPY package (which provides many numerical methods, e.g., matrix diagonalization) should be available. If NUMPY is not available, some parts of the SHARC suite are still functional, and the affected scripts will fall back to use a small Fortran code (front-end for LAPACK) within the SHARC package. Since in the Python scripts no large-scale matrix calculations are carried out, there should be no significant performance loss if NUMPY is not available.
NUMPY is mandatory for dynamics with the ADF interface, with LVC models, and all pysharc functionalities. - The Python package MATPLOTLIB.If the MATPLOTLIB package, some auxiliary scripts (trajana_nma.py and trajana_essdyn.py) can automatically generate certain plots.
- The GNUPLOT plotting software.GNUPLOT is not strictly necessary, since all output files could be plotted using other plotting programs. However, a number of scripts from the SHARC suite automatically generate GNUPLOT scripts after data processing, allowing to quickly plot the results.
- A molecular visualization software able to read xyz files (e.g. MOLDEN, GABEDIT, MOLEKEL or VMD).Molecular visualization software is needed in order to animate molecular motion in the dynamics.
- The THEODORE wave function analysis suite (version 2.0 or higher).The wave function analysis package THEODORE allows to compute various descriptors of electronic wave functions (supported by some interfaces), which is helpful to follow the state characters along trajectories.
- The AMBER molecular dynamics package.AMBER can be used to prepare initial conditions based on ground state molecular dynamics simulations (instead of using a Wigner distribution), which is especially useful for large systems.
- The ORCA ab initio package.ORCA can be employed as external optimizer. In combination with the SHARC interfaces, it is possible to perform optimizations of minima, conical intersections, and crossing points for any method interfaced to SHARC.
2.3.5 Quantum Chemistry Programs
Even though SHARC comes with two interfaces for analytical potentials (and hence can be used without any quantum chemistry program), the main application of SHARC is certainly on-the-fly ab initio dynamics. Hence, one of the following interfaced quantum chemistry programs is necessary:
- MOLPRO (this release was checked against MOLPRO 2010 and 2012).
- OPENMOLCAS (this release was checked against OPENMOLCAS 22).
- TINKER, interfaced to OPENMOLCAS 22, for QM/MM dynamics.
- MOLCAS (this release was checked against MOLCAS 8.3 and 8.4).
- TINKER, interfaced to MOLCAS, for QM/MM dynamics.
- COLUMBUS 7
- COLUMBUS-MOLCAS interface for spin-orbit couplings.
- AMSTERDAM DENSITY FUNCTIONAL (only ADF 2019 or newer)
- TURBOMOLE (this release was checked against TURBOMOLE 6.6, 7.0, 7.1, 7.2, 7.3, and 7.4).
- GAUSSIAN (this release was checked against GAUSSIAN 09 and 16).
- ORCA (version 4.1, 4.2, or 5.0).
- TINKER (this release was checked against version 6.3.3) for QM/MM dynamics.
- BAGEL (commit 0ea6b59 from Mar 27, 2019 or newer).
- PyQuante for overlap calculations
See the relevant sections in chapter 6 for a description of the quantum chemical methods available with each of these programs.
Chapter 3
Execution
The SHARC suite consists of the main dynamics code sharc.x and a number of auxiliary programs, like setup scripts and analysis tools. Additionally, the suite comes with interfaces to several quantum chemistry software: MOLPRO, MOLCAS, COLUMBUS, TURBOMOLE, ADF, GAUSSIAN, ORCA, and BAGEL.
In the following, first it is explained how to run a single trajectory by setting up all necessary input for the dynamics code sharc.x manually. Afterwards, the usage of the auxiliary scripts is explained.
Detailed infos on the SHARC input files is given in chapter 4.
Chapter 5 documents the different output files SHARC produces.
The interfaces are described in chapter 6 and the auxiliary scripts in chapter 7.
All relevant theoretical background is given in chapter 8.
3.1 Running a single trajectory
3.1.1 Input files
SHARC requires a number of input files, which contain the settings for the dynamics simulation (input), the initial geometry (geom), the initial velocity (veloc), the initial coefficients (coeff) and the laser field (laser). Only the first two (input, geom) are mandatory, the others are optional. The necessary files are shown in figure 3.1.
The content of the main input file is explained in detail in section 4.1, the geometry file is specified in section 4.2. The specifications of the velocity, coefficient and laser files are given in sections 4.3, 4.4 and 4.5, respectively.
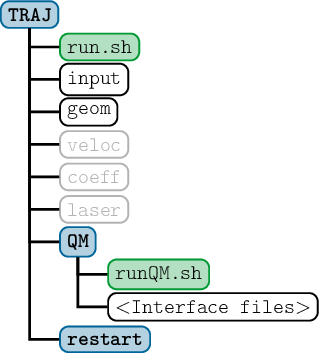
Additionally, the directory QM/ and the script QM/runQM.sh need to be present, since the on-the-fly ab initio calculations are implemented through these files. The script QM/runQM.sh is called each time SHARC performs an on-the-fly calculation of electronic properties (usually by a quantum chemistry program). In order to do so, SHARC first writes the request for the calculation to QM/QM.in, then calls QM/runQM.sh, waits for the script to finish and then reads the requested quantities from QM/QM.out. The script QM/runQM.sh is fully responsible to generate the requested results from the provided input.
In virtually all cases, this task is handled by the SHARC-quantum chemistry interfaces (see chapter 6), so that the script QM/runQM.sh has a particularly simple form:
cd QM/
$SHARC/<INTERFACE> QM.in
with the corresponding interface name given. Note that the interfaces in all cases need additional input files, which must be present in QM/. Those input files contain the specifications for the quantum chemistry information, e.g., basis set, active and reference space, memory settings, path to the quantum chemistry program, path to scratch directories; or for SHARC_Analytical.py and SHARC_LVC.py the parameters for the analytical potentials. For each interface, the input files are slightly different. See sections 6.3, 6.4, 6.5, 6.6, 6.8, 6.7, 6.9, 6.10, 6.11, or 6.12 for the necessary information.
3.1.2 Running the dynamics code
Given the necessary input files, SHARC can be started by executing
user@host> $SHARC/sharc.x input
Note that besides the input file, at least the geometry file needs to be present (see chapter 4 for details).
A running trajectory can be stopped after the current time step by creating an empty file STOP:
user@host> touch STOP
This is usually preferable to simply killing SHARC, because the current time step is properly finished and all files are correctly written for analysis and restart.
3.1.3 Output files
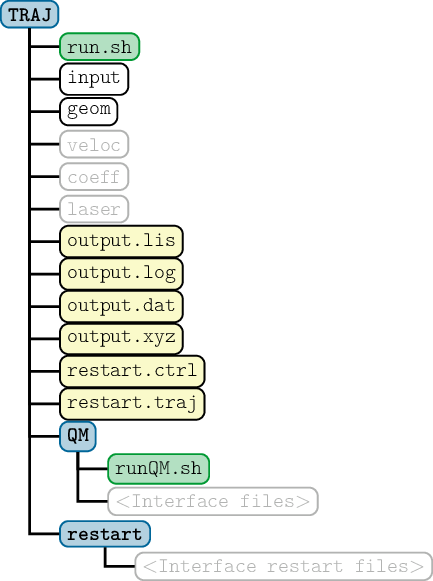
Figure 3.2 shows the content of a trajectory directory after the execution of SHARC. There will be six new files. These files are output.log, output.lis, output.dat and output.xyz, as well as restart.ctrl and restart.traj.
The file output.log contains mainly a listing of the chosen options and the resulting dynamics settings. At higher print levels, the log file contains also information per time step (useful for debugging). output.lis contains a table with one line per time step, giving active states, energies and expectation values. output.dat contains a list of all important matrices and vectors at each time step. This information can be extracted with data_extractor.x to yield plottable table files. output.xyz contains the geometries of all time steps (the comments to each geometry give the active state).
For details about the content of the output files, see chapter 5.
The restart files contain the full state of a trajectory and its control variables from the last successful time step. These files are needed in order to restart a trajectory at this time step (either because the calculation failed, or in order to extend the simulation time beyond the original maximum simulation time).
The restart/ directory contains all persistent files that are needed for the quantum chemistry interfaces (for restarting, but also between all time steps).
3.2 Typical workflow for an ensemble of trajectories
Usually, one is not interested in running only a single trajectory, since a single trajectory cannot reproduce the branching of a wave packet into different reaction channels. In order to do so, within surface hopping an ensemble of independent trajectories is employed.
When dealing with a (possibly large) ensemble of trajectories, setup and analysis need to be automatized. Hence, the SHARC suite contains a number of scripts fulfilling different tasks in the usual workflow of setting up ensembles of trajectories.
The typical workflow is given schematically in figure 3.3.
3.2.1 Initial condition generation
In the typical workflow, the user will first create a set of suitable initial conditions. In the context of the SHARC package, an initial condition is a set of an initial geometry, initial velocity, initial occupied state and initial wave function coefficients.
Many such sets are needed in order to setup physically sound dynamics simulations.
Generation of initial geometries and velocities
Currently, within the SHARC suite, initial geometries and velocities can be generated based on a quantum harmonic oscillator Wigner distribution. The theoretical background is given in section 8.24. The calculation is performed by wigner.py, which is explained in section 7.1.
As given in figure 3.3, wigner.py needs as input the result of a frequency calculation in MOLDEN format. The calculation can be performed by any quantum chemistry program and any method the user sees fit (there are some scripts which can aid in the frequency calculation, see sections 6.3.5, 6.4.3, 6.7.6).
wigner.py produces the file initconds, which contains a list of initial conditions ready for further processing.
Alternatively, initial geometries and velocities can be extracted from molecular dynamics simulations in the ground state.
Currently, it is possible to either convert restart files AMBER to an initconds file (using amber_to_initconds.py, see section 7.3) or to randomly sample snapshots from SHARC trajectories (using sharctraj_to_initconds.py, see section 7.4).
Generation of initial coefficients and states
In the second preparation step, for each of the sampled initial geometries it has to be decided which excited state should be the initial one. In simple cases, the user may manually choose the initial excited state using excite.py (optionally after diabatization; see 7.6). Alternatively, the selection of initial states can be performed based on the excitation energies and oscillator strengths of the excited states at each initial geometry (this approximately simulates a delta-pulse excitation).
The latter options (diabatization or energies/oscillator strengths) make it necessary to carry out vertical excitation calculation before the selection of the initial states.
The calculations can be set up with setup_init.py (see section 7.5). This script prepares for each initial condition in the initconds file a directory with the necessary input to perform the calculation. The user should then execute the run script (run.sh) in each of the directories (either manually or through a batch queueing system).
After the vertical excitation calculations are completed, the vertical excitation energies and oscillator strengths of each calculation are collected by excite.py (see 7.6). The same script then performs the selection of the initial electronic state for each initial geometry. The results are written to a new file, initconds.excited. This file contains all information needed to setup the ensemble.
Additionally, spectrum.py (7.9) can calculate absorption spectra based on the initconds.excited file. This may be useful to verify that the level of theory chosen is appropriate (e.g., by comparing to an experimental spectrum), or to choose a suitable excitation window for the determination of the initial state.
3.2.2 Running the dynamics simulations
Based on the initial conditions given in initconds.excited, the input for all trajectories in the ensemble can be setup by setup_traj.py (see section 7.7). The script produces one directory for each trajectory, containing the input files for SHARC and the selected interface.
In order to run a particular trajectory, the user should execute the run script (run.sh) in the directory of the trajectory. Since those calculations can run between minutes and several weeks (depending on the level of theory used and the number of time steps), it is advisable to submit the run scripts to a batch queueing system.
The progress of the simulations can be monitored most conveniently in the output.lis files. If the calculations are running in some temporary directory, the output files can be copied to the local directory (where they were setup) with the scp wrapper retrieve.sh (see 7.10). This allows to perform ensemble analysis while the trajectories are still running.
If a trajectory fails, the temporary directory where the calculation is running is not deleted. The file README will be created in the trajectory’s directory, giving the time of the failure and the location of the temporary data, so that the case can be investigated.
In order to signal SHARC to terminate a trajectory after the current time step is completed, the user can create a (possibly empty) file STOP in the working directory of the trajectory (the directory where sharc.x is running).
The status of the ensemble of trajectories can be checked with diagnostics.py (section 7.15). This script checks the presence and integrity of all relevant files, the progress of all trajectories, and warns if trajectories behave unexpectedly (non-conversion of total energy, intruder states, etc).
3.2.3 Analysis of the dynamics results
Each trajectory can be analyzed independently by inspecting the output files (see chapter 5). Most importantly, calling data_extractor.x (7.11) on the output.dat file of a trajectory creates a number of formatted files which can be plotted with the help of make_gnuscript.py (7.14) and GNUPLOT.
The nuclear geometries in output.xyz file can be analyzed in terms of internal coordinates (bond lengths, angles, ring conformations, etc.) using geo.py (7.22).
The manual analysis of all individual trajectories is usually a good idea to verify that the trajectories are correctly executing, and in order to find general reaction pathways.
The manual analysis often permits to formulate some hypotheses, which can then be verified with the statistical analysis tools.
For the complete ensemble, the first step should usually be to run diagnostics.py (section 7.15).
This script will determine how long the different trajectories are, and, more importantly, will check the trajectories for file integrity, conservation of total energy, and continuity of potential/kinetic energy.
Based on a set of customizable criteria, the script determines for each trajectory a “maximum usable time”.
The script then can mark all trajectories with maximum usable time below a given threshold to be excluded from analysis (by creating a file DONT_ANALYZE in the trajectory’s directory).
The other analysis scripts will then ignore trajectories marked by diagnostics.py.
Trajectories can also be manually excluded from analysis, by creating a file called CRASHED, DEAD, or RUNNING in the respective directory.
After the trajectories were checked and unsuitable ones excluded, the statistical analysis scripts can be used.
The script populations.py (section 7.16) can calculate average excited-state populations.
The script transition.py (section 7.17) can analyze the total number of hops between all pairs of states in an ensemble, allowing to identify relevant relaxation routes in the dynamics.
Using the script make_fit.py (7.18), it is possible to make elaborate global fits of chemical kinetics models to the populations data, allowing to extract rate constants from the populations, and to compute errors for these rate constants.
The same functionality is also present in the older scripts make_fitscript.py (7.19) and bootstrap.py (7.20).
The script crossing.py (7.21) can find and extract notable geometries, e.g., those geometries where a surface hop between two particular states occurred.
Using trajana_essdyn.py (7.23) and trajana_nma.py (7.24) it is furthermore possible to perform essential dynamics analysis and normal mode analysis.
Finally, data_collector.py can merge arbitrary tabulated data from the trajectories and perform various analysis procedures (compute mean/standard deviation, data convolution, summation, integration), which can be used to compute, e.g., time-dependent distribution functions or time-dependent spectra.
3.3 Auxilliary Programs and Scripts
The following tables list the auxiliary programs in the SHARC suite. The rightmost column gives the section where the program is documented.
3.3.1 Setup
| wigner.py | Creates initial conditions from Wigner distribution. | 7.1 |
| state_selected.py | Creates initial conditions from selected vibrational state. | 7.2 |
| amber_to_initconds.py | Creates initial conditions from Amber restart files. | 7.3 |
| sharctraj_to_initconds.py | Creates initial conditions from SHARC trajectories. | 7.4 |
| setup_init.py | Sets up initial vertical excitation calculations. | 7.5 |
| excite.py | Generates excited state lists for initial conditions and selects initial states. | 7.6 |
| setup_traj.py | Sets up the dynamics simulations based on the initial conditions. | 7.7 |
| laser.x | Prepares files containing laser fields. | 7.8 |
| molpro_input.py | Prepares MOLPRO input files and template files for the MOLPRO interface. | 6.3.5 |
| molcas_input.py | Prepares MOLCAS input files and template files for the MOLCAS interface. | 6.4.3 |
| ADF_input.py | Prepares ADF input files. | 6.7.5 |
| ADF_freq.py | Converts ADF output files of frequency calculations to Molden format. | 6.7.6 |
| setup_LVCparam.py | Sets up single point calculations for LVC parametrization. | 6.9.2 |
| create_LVCparam.py | Produces LVC model files from parametrization data. | 6.9.2 |
3.3.2 Analysis
| spectrum.py | Generates absorption spectra from initial conditions files. | 7.9 |
| retrieve.sh | scp wrapper to retrieve dynamics output during the simulation. | 7.10 |
| data_extractor.x | Extracts plottable results from the SHARC output data file. | 7.11 |
| data_extractor_NetCDF.x | Extracts plottable results from the SHARC output data file in NetCDF format. | 7.12 |
| data_converter.x | Converts output.dat files to output.dat.nc files. | 7.13 |
| make_gnuscript.py | Creates gnuplot scripts to plot trajectory data. | 7.14 |
| diagnostics.py | Checks ensembles for integrity, progress, energy conservation. | 7.15 |
| populations.py | Calculates ensemble populations. | 7.16 |
| transition.py | Calculates total number of hops within an ensemble. | 7.17 |
| make_fit.py | Performs kinetic model fits and bootstrapping. | 7.18 |
| make_fitscript.py | Creates GNUPLOT scripts to fit kinetic models to population data. | 7.19 |
| bootstrap.py | Computes errors for kinetic model fits. | 7.20 |
| crossing.py | Extracts specific geometries from ensembles. | 7.21 |
| geo.py | Calculates internal coordinates from xyz files. | 7.22 |
| trajana_essdyn.py | Performs an essential dynamics analysis for an ensemble. | 7.23 |
| trajana_nma.py | Performs a normal mode analysis for an ensemble. | 7.24 |
| data_collector.py | Collects data from tabular files and performs various analyses | 7.25 |
3.3.3 Interfaces
| SHARC_MOLPRO.py | Calculates SOCs, gradients, nonadiabatic couplings, overlaps, dipole moments, and Dyson norms at the CASSCF level of theory (using MOLPRO). Symmetry or RASSCF are not supported. Only segmented basis sets are possible. | 6.3 |
| SHARC_MOLCAS.py | Calculates SOCs, gradients, overlaps, dipole moments, Dyson norms, dipole moment derivatives, and spin-orbit coupling derivatives at the CASSCF and (MS-)CASPT2 level of theory (using MOLCAS). Further supported methods are XMS-PDFT, and CMS-PDFT. Symmetry is not supported. Numerical differentiation is used for some tasks. | 6.4 |
| SHARC_COLUMBUS.py | Calculates SOCs, gradients, nonadiabatic couplings, overlaps, dipole moments, and Dyson norms at the CASSCF, RASSCF, and MRCISD levels of theory (using COLUMBUS). Symmetry is not supported. Works with the either DALTON or SEWARD integrals (through the COLUMBUS– MOLCAS interface), but SOCs are only available with SEWARD integrals. Nonadiabatic couplings are only available with DALTON integrals. | 6.5 |
| SHARC_Analytical.py | Calculates SOCs, gradients, overlaps, dipole moments, and dipole moment derivatives based on analytical expressions of diabatic matrix elements defined in Cartesian coordinates. | 6.6 |
| SHARC_ADF.py | Calculates SOCs, gradients, overlaps, dipole moments, and Dyson norms at the TD-DFT level of theory with GGA and hybrid functionals (using ADF). Symmetry is not supported. | 6.7 |
| SHARC_RICC2.py | Calculates SOCs, gradients, overlaps, and dipole moments at the ADC(2) and CC2 levels of theory (using TURBOMOLE). Symmetry is not supported. For SOCs, only ADC(2) can be used and ORCA (only version 4 currently) has to be installed in addition to TURBOMOLE. | 6.8 |
| SHARC_LVC.py | Calculates SOCs, gradients, nonadiabatic couplings, overlaps, and dipole moments based on linear-vibronic coupling models defined in mass-weighted normal mode coordinates. | 6.9 |
| SHARC_GAUSSIAN.py | Calculates gradients, overlaps, dipole moments, and Dyson norms at the TD-DFT level of theory (using Gaussian). Symmetry is not supported. | 6.10 |
| SHARC_ORCA.py | Calculates SOCs, gradients, overlaps, dipole moments, and Dyson norms at the TD-DFT level of theory with GGA and hybrid functionals (using ORCA). Symmetry is not supported. | 6.11 |
| SHARC_BAGEL.py | Calculates gradients, nonadiabatic couplints, overlaps, dipole moments, and Dyson norms at the CASSCF, CASPT2, MS-CASPT2, and XMS-CASPT2 level of theory (using BAGEL). Symmetry is not supported. | 6.12 |
3.3.4 Others
| tests.py | Script to automatically run the SHARC test suite. | 2.3.3 |
| wfoverlap.x | Program to compute wave function overlaps, used by most interfaces. | 6.13 |
| Orca_External | Script to carry out optimizations with ORCA as optimizer and SHARC as gradient provider. | 7.26 |
| setup_orca_opt.py | Script to setup optimizations with ORCA as optimizer and SHARC as gradient provider. | 7.26 |
| setup_single_point.py | Script to setup single point calculations with SHARC interfaces. | 7.27 |
| QMout_print.py | Script to convert a QM.out file to a table with energies and oscillator strengths. | 7.28 |
| diagonalizer.x | Helper program for excite.py. Only required if NUMPY is not available. | 7.29 |
3.4 The PYSHARC dynamics driver
Since SHARC2.1, the suite contains alternative dynamics drivers, besides the regular sharc.x executable, which are based on the pysharc sub-project.
pysharc is an implementation of the SHARC dynamics driver in Python that directly calls the Fortran routines of sharc.x (through the Python-C API via intermediate C routines).
In this way, both the sharc.x code and the quantum chemistry interface code can be run within the same program, omitting file-based communication between driver and quantum chemistry interface.
The motivation of this is that the omission of file-based communication can save up to a few seconds in each time step.
Naturally, this is negligible for expensive quantum chemistry where a time step takes several minutes.
However, for very fast interfaces (analytical models, LVC models), time steps can be reduced from a few seconds to a few milliseconds, providing a dramatic speedup of the SHARC simulations which is only limited by the speed of writing the output files.
Consequently, the use of pysharc is highly advisable for SHARC simulations with very fast interfaces.
Currently, pysharc is only implemented for LVC models, through the driver script named pysharc_lvc.py.
pysharc is intended to change the SHARC workflow as little as possible.
Basically all features of sharc.x are supported.
The only change that needs to be applied is to call the pysharc driver instead of sharc.x.
The high efficiency of pysharc is optimally combined with an efficient way of producing output.
As the default ASCII output format is not optimized for performance, together with pysharc SHARC3.0 contains an implementation that produces NetCDF binary output data files.
It is advisable that every time pysharc is run, output is written in NetCDF format.
Details of NetCDF output are documented in Section 5.4
Note that in SHARC3.0, some new options (adaptive time steps, time uncertainty hopping, decay of mixing decoherence, and Ehrenfest dynamics) are not
Chapter 4
Input files
In this chapter, the format of all SHARC input files are presented. Those are the main input file (here called input), the geometry file, the velocity file, the coefficients file, the laser file, and the atom mask file. Only the first two are mandatory, the others are optional input files. All input files are ASCII text files.
4.1 Main input file
This section presents the format and all input keywords for the main SHARC input. Note that when using setup_traj.py, full knowledge of the SHARC input keywords is not required.
4.1.1 General remarks
The input file has a relatively flexible structure. With very few exceptions, each single line is independent. An input line starts with a keyword, followed optionally by a number of arguments to this keyword. Example:
stepsize 0.5
Here, stepsize is the keyword, referring to the size of the time steps for the nuclear motion in the dynamics. 0.5 gives the size of this time step, in this example 0.5 fs.
A number of keywords have no arguments and act as simple switches (e.g., restart, gradcorrect, grad_select, nac_select, ionization, track_phase, dipole_gradient). Those keywords can be prefixed with no to explicitly deactivate the option (e.g., norestart deactivates restarts).
In each line a trailing comment can be added in the input file, by using the special character #. Everything after # is ignored by the input parser of SHARC. The input file also can contain arbitrary blank lines and lines containing only comments. All input is case-insensitive.
The input file is read by SHARC by subsequently searching the file for all known keywords. Hence, unknown or misspelled keywords are ignored. Also, the order of the keywords is completely arbitray. Note however, that if a keyword is repeated in the input only the first instance is used by the program.
4.1.2 Input keywords
In Table 4.1, all input keywords for the SHARC input file are listed.
|
Table 4.1: Input keywords for sharc.x. The first column gives the name of the keyword, the second lists possible arguments and the third line provides an explanation. Defaults are marked like this. $n denotes the n-th argument to the keyword.
|
|||
| Keyword | Arguments | Explanation | |
| printlevel | integer | Controls the verbosity of the log file. | |
| $1=0 | Log file is empty | ||
| $1=1 | + List of internal steps | ||
| $1=2 | + Input parsing information | ||
| $1=3 | + Some information per time step | ||
| $1=4 | + More information per time step | ||
| $1=5 | + Much more information per time step | ||
| restart | Dynamics is resumed from restart files. | ||
| norestart | Dynamics is initialized from input files. | ||
| norestart takes precedence. | |||
| restart_rerun_last_qm_step | Use when restarting after non-graceful stop/crash. | ||
| restart_goto_new_qm_step | Use when restarting after reaching time limit, using STOP file, or killafter keyword. | ||
| No default, an error is raised if neither is present during restart. | |||
| rngseed | integer | Seed for the random number generator. | |
| 10997279 | Used for surface hopping and AFSSH decoherence. | ||
| compatibility | $1=0 | Compatibility mode disabled. | |
| $1=1 | Do not draw a second random number per step (for decoherence). | ||
| – Input file keywords – | |||
| geomfile | quoted string | File name containing the initial geometry. | |
| “geom” | |||
| velocfile | quoted string | File containing the initial velocities. | |
| “veloc” | Only read if veloc external. | ||
| coefffile | quoted string | File containing the initial wave function coefficients. | |
| “coeff” | Only read if coeff external. | ||
| laserfile | quoted string | File containing the laser field. | |
| “laser” | Only read if laser external. | ||
| atommaskfile | quoted string | File containing the atom mask. | |
| ätommask” | Only read if atommask external. | ||
| rattlefile | quoted string | File containing the list of bond length constraints. | |
| “rattle” | Only read if rattle. | ||
| – Trajectory initialization keywords – | |||
| veloc | string | Sets the initial velocities. | |
| $1=zero | Initial velocities are zero. | ||
| $1=random $2 float | Random initial velocities with $2 eV kinetic energy per atom. | ||
| $1=external | Initial velocities are read from file. | ||
| nstates | list of integers | Number of states per multiplicity. | |
| $1 (1) | Number of singlet states | ||
| $2 (0) | Number of doublet states | ||
| $3 (0) | Number of triplet states | ||
| $… (0) | Number of states of higher multiplicities | ||
| actstates | list of integers | Number of active states per multiplicity. | |
| same as nstates | By default, all states are active. | ||
| state | integer, string | Specifies the initial state. | |
| (no default; SHARC exits if state is missing). | |||
| $1 | Initial state. | ||
| $2=MCH | Initial state and coefficients are given in MCH representation. | ||
| $2=diag | Initial state and coefficients are given in diagonal representation. | ||
| coeff | string | Sets the wave function coefficients. | |
| $1=auto | Initial coefficient are determined automatically from initial state. | ||
| $1=external | Initial coefficients are read from file. | ||
| – Laser field keywords – | |||
| laser | string | Sets the laser field. | |
| $1=none | No laser field is applied. | ||
| $1=internal | Laser field is calculated at each time step from internal function. | ||
| $1=external | Laser field for each time step is read during initialization. | ||
| laserwidth | float | Laser bandwidth used to detect induced hops. | |
| 1.0 eV | |||
| – Time step keywords – | |||
| stepsize | float | Length of the nuclear dynamics time steps in fs. | |
| 0.5 fs | |||
| nsubsteps | integer | Number of substeps for the integration of the electronic equation of motion. | |
| 25 | |||
| nsteps | integer | Number of simulation steps. | |
| 3 | |||
| tmax | float | Total length of the simulation in fs. | |
| No effect if nsteps is present. | |||
| killafter | float | Terminates the trajectory after $1 fs in the lowest state. | |
| -1 | If $1 < 0, trajectories are never killed. | ||
| – Integrator keywords – | |||
| integrator | string | Method to control the integrator. | |
| $1=fvv | Fixed time step velocity Verlet integrator. | ||
| $1=avv | Adaptive time step velocity Verlet integrator (not in pysharc). | ||
| convthre | float | Convergence threshold for adaptive integrators (in eV). | |
| $1=1e-04 | |||
| stepsize_min | float | Minimum step size allowed in adaptive velocity Verlet. | |
| $1=stepsize/16 | |||
| stepsize_max | float | Maximum step size allowed in adaptive velocity Verlet. | |
| $1=stepsize*2 | |||
| stepsize_min_exp | integer | Minimum order of 2 allowed in adjusting the time step in adaptive velocity Verlet. If used, this keyword will overwrite keyword stepsize_min. | |
| $1=-4 | |||
| stepsize_max_exp | integer | Maximum order of 2 allowed in adjusting the time step in adaptive velocity Verlet. If used, this keyword will overwrite keyword stepsize_max. | |
| $1=2 | |||
| – Dynamics setting keywords that applicable to both TSH and SCP methods – | |||
| method | string | Nonadiabatic dynamics method. | |
| $1=tsh | Uses trajectory surface hopping. | ||
| $1=scp, ehrenfest | Uses self-consistent potential methods. | ||
| coupling | string | Quantities describing the nonadiabatic couplings. | |
| $1=ddr,nacdr | Uses vectorial nonadiabatic couplings 〈ψα|∂/∂R|ψβ〉. | ||
| $1=ddt,nacdt | Uses temporal nonadiabatic couplings 〈ψα|∂/∂t|ψβ〉. | ||
| $1=overlap | Uses the overlaps 〈ψα(t0)|ψβ(t)〉 (local diabatization). | ||
| $1=ktdc | Uses curvature driven approximation for time derivative coupling. | ||
| ktdc_method | string | Method to compute curvature driven approximated time derivative coupling. | |
| $1=energy | Second order finite difference of energy (default for TSH). | ||
| $1=gradient | First order finite difference of dot product of gradients and velocity vector (default for SCP). | ||
| eeom | string | Method to control the propagator of electronic equation of motion. We suggest the users use default options. | |
| $1=ci | Constant interpolation. | ||
| $1=li | Linear interpolation. This is the default when set coupling=ddr or coupling=ktdc. | ||
| $1=ld | Local diabatization. This is the default when set coupling=overlap and method=tsh. | ||
| $1=npi | Norm preserving interpolation.[115] This is the default when set coupling=overlap and method=scp. | ||
| gradcorrect | empty or string | Include NACs in gradient transformation. | |
| $1=none, ngt, nac | Include (Eα−Eβ)〈ψα|∂/∂R|ψβ〉 in gradient transformation. | ||
| $1=tdm, kmatrix | Include (Eα−Eβ)〈ψα|∂/∂t|ψβ〉 in gradient transformation. | ||
| nogradcorrect | Transform only the gradients. | ||
| tdm_method | string | Method to control the computations of time derivative of potential energies in diagonal basis in TDM gradient correction scheme. | |
| $1=gradient | Time derivative of potential energies in diagonal basis are computed from transformation of time derivative matrix in MCH basis. And the time derivative of potential energies in MCH basis are computed by a dot product between nuclear gradient vector and velocity vector. This is the default option for coupling=ddr or coupling=overlap. | ||
| $1=energy | Time derivative of potential energies in diagonal basis are computed from finite difference. This is more accurate for curvature driven methods because in curvature-driven algorithms we approximate TDCs instead of computing TDCs accurately form electronic structure software. This is the default option for coupling=ktdc. | ||
| decoherence_scheme | string | Method for decoherence correction. | |
| $1=none | No decoherence correction. | ||
| $1=edc | Energy-difference based correction.[116] | ||
| $1=afssh | Augmented FSSH.[30] | ||
| $1=dom | Add decay-of-mixing decoherence to SCP methods to perform CSDM or SCDM.[91,[92] Not usable for TSH. | ||
| decoherence | Applies decoherence correction (defaults are EDC for TSH methods and Decay-of-Mixing for SCP methods). | ||
| nodecoherence | No decoherence correction. | ||
| nodecoherence takes precedence. | |||
| – Surface hopping setting keywords – | |||
| surf | string | Potential energy surfaces used in TSH. No effect for SCP. | |
| $1=diagonal,sharc | Uses diagonal potentials. | ||
| $1=MCH | Uses MCH potentials. | ||
| ekincorrect | string | Adjustment of the kinetic energy after a surface hop. | |
| $1=none | Kinetic energy is not adjusted. Jumps are never frustrated. | ||
| $1=parallel_vel | Velocity is rescaled to adjust kinetic energy. | ||
| $1=parallel_pvel | Only the velocity component in the direction of vibrational motion is rescaled. | ||
| $1=parallel_nac | Only the velocity component in the direction of 〈ψα|∂/∂R|ψβ〉 is rescaled. | ||
| $1=parallel_diff | Only the velocity component in the direction of ∆∇E is rescaled. | ||
| $1=parallel_pnac | Only the velocity component in the direction of projected 〈ψα|∂/∂R|ψβ〉 is rescaled. The projection ensures conservation of nuclear orbital angular momentum and center of mass motion[95] | ||
| $1=parallel_enac | Only the velocity component in the direction of effective nonadiabatic coupling vector is rescaled.[93] | ||
| $1=parallel_penac | Only the velocity component in the direction of projected effective nonadiabatic coupling vector is rescaled.[93,[95] | ||
| reflect_frustrated | string | Reflection of trajectory after frustrated hop. | |
| $1=none | No reflection. | ||
| $1=parallel_vel | Full velocity vector is reflected. | ||
| $1=parallel_pvel | Only the velocity component in the direction of vibrational motion is reflected. | ||
| $1=parallel_nac | Only the velocity component in the direction of 〈ψα|∂/∂R|ψβ〉 is reflected. | ||
| $1=parallel_diff | Only the velocity component in the direction of ∆∇E is reflected. | ||
| $1=parallel_pnac | Only the velocity component in the direction of projected 〈ψα|∂/∂R|ψβ〉 is reflected. The projection ensures conservation of nuclear orbital angular momentum and center of mass motion[95] | ||
| $1=parallel_enac | Only the velocity component in the direction of effective nonadiabatic coupling vector is reflected.[93] | ||
| $1=parallel_penac | Only the velocity component in the direction of projected effective nonadiabatic coupling vector is reflected.[93,[95] | ||
| $1=delV_vel | Full velocity vector is reflected according to ∇V criteria.[117] | ||
| $1=delV_pvel | Only the velocity component in the direction of vibrational motion is reflected according to ∇V criteria. | ||
| $1=delV_nac | Only the velocity component in the direction of 〈ψα|∂/∂R|ψβ〉 is reflected according to ∇V criteria. | ||
| $1=delV_diff | Only the velocity component in the direction of ∆∇E is reflected according to ∇V criteria. | ||
| $1=delV_pnac | Only the velocity component in the direction of projected 〈ψα|∂/∂R|ψβ〉 is reflected according to ∇V criteria. | ||
| $1=delV_enac | Only the velocity component in the direction of effective nonadiabatic coupling vector is reflected according to ∇V criteria. | ||
| $1=delV_penac | Only the velocity component in the direction of projected effective nonadiabatic coupling vector is reflected according to ∇V criteria. | ||
| hopping_procedure | string | Method for hopping probabilities. | |
| $1=off | No hops (same as no_hops). | ||
| $1=sharc,standard | Standard SHARC hopping probabilities. | ||
| $1=gfsh | Global flux SH hopping probabilities.[71] | ||
| no_hops | Disables surface hopping. | ||
| no_hops takes precedence over hopping_procedure. | |||
| force_hop_to_gs | float | Activates forced hops to lowest state. | |
| hop is forced if lowest-active energy difference < $1 | |||
| time_uncertainty | Employ fewest switches with time uncertainty algorithm in TSH to reduce the number of frustrated hops. | ||
| decoherence_param | float | Value α in EDC (in Hartree). | |
| 0.1 | $1 > 0.0 | ||
| atommask | string | Activates masking of atoms (for EDC, parallel_vel). | |
| $1=none | No atoms are masked. | ||
| $1=external | Atom mask is read from external file. | ||
| – Self-consistent potential methods setting keywords – | |||
| neom | string | Methods to control the direction of the nonadiabatic force in nuclear equation of motion for SCP methods. | |
| $1=ddr,nacdr | Use full nonadiabatic coupling vector. This is the default when coupling=ddr. | ||
| $1=gdiff | Use effective nonadiabatic coupling vector, which is a combination of difference gradient vector and velocity vector. This is the default when coupling=overlap or coupling=ktdc. | ||
| pointer_basis | string | Methods to control the pointer basis employed in decay-of-mixing algorithms. We suggest use the default option. | |
| $1=diag | Use the diagonal basis as the pointer basis. | ||
| $1=MCH | Use the MCH basis as the pointer basis. | ||
| switching_procedure | string | Methods for scheme used to switch the pointer state in decay-of-mixing algorithms. | |
| $1=csdm | Using coherent switching with decay of mixing. [91,[92] | ||
| $1=scdm | Using self-consistent decay of mixing. [118] | ||
| nac_projection | Applies projection on the direction of the nonadiabatic force in nuclear equation of motion for SCP methods. This is the default option that ensures conservation of nuclear orbital angular momentum and center of mass motion. | ||
| nonac_projection | Do not apply projection on the direction of nonadiabatic force in nuclear equation of motion for SCP methods. | ||
| decoherence_param_alpha | float | Value α in decay of mixing decoherence time (in Hartreee). | |
| 0.1 | $1 > 0.0 | ||
| decoherence_param_beta | float | Value β in decay of mixing decoherence time (unitless). | |
| 1.0 | $1>0.0 | ||
| – Constraints – | |||
| rattle | Enables bond length constraints through RATTLE. | ||
| norattle | No RATTLE. | ||
| norattle takes precedence. | |||
| rattletolerance | float | Convergence criterion for RATTLE. | |
| 1e-7 | $1 > 0.0 | ||
| – Energy control keywords – | |||
| ezero | float | Energy shift for Hamiltonian diagonal elements (Hartree). | |
| 0.0 | Is not determined automatically! | ||
| scaling | float | Scaling factor for Hamiltonian matrix and gradients. | |
| 1.0 | 0. < $1 | ||
| soc_scaling | float | Scaling factor for spin-orbit coupling. | |
| 1.0 | 0. < $1 | ||
| dampeddyn | float | Scaling factor for kinetic energy at each time step. | |
| 1.0 | 0. ≤ $1 ≤ 1. | ||
| – Gradient and NAC selection keywords – | |||
| grad_select | Only some gradients are calculated at every time step. | ||
| grad_all | All gradients are calculated at every time step (Alias: nograd_select). | ||
| grad_all takes precedence. | |||
| nac_select | Only some 〈ψα|∂/∂R|ψβ〉 are calculated at every time step. | ||
| nac_all | All 〈ψα|∂/∂R|ψβ〉 are calculated at every time step (Alias: nonac_select). | ||
| nac_all takes precedence. | |||
| eselect | float | Parameter for selection of gradients and NACs (in eV). | |
| 0.5 eV | |||
| select_directly | Do not do a second QM calculation for gradients and NACs. | ||
| noselect_directly | Do a second QM calculation for gradients and NACs. | ||
| – Phase tracking keywords – | |||
| track_phase | Track the phase of the transformation matrix U. | ||
| notrack_phase | No phase tracking of U (can provide very large speedups in pysharc, but check whether results are affected). | ||
| phases_from_interface | Request phase information from interface. | ||
| nophases_from_interface | Try to recover phase information from QM data. | ||
| phases_at_zero | Request phase from interface at t=0. | ||
| – Property computation keywords – | |||
| spinorbit | Include spin-orbit couplings into the Hamiltonian. | ||
| nospinorbit | Neglect spin-orbit couplings. | ||
| dipole_gradient | Include dipole moments derivatives in the gradients. | ||
| nodipole_gradient | Neglect dipole moments derivatives. | ||
| ionization | Calculate ionization probabilities on-the-fly. | ||
| noionization | No ionization probabilities. | ||
| ionization_step | integer | Calculate ionization probabilities every $1 time step. | |
| 1 | By default calculated every time step (if ionization). | ||
| theodore | Calculate wavefunction descriptors on-the-fly. | ||
| notheodore | No wavefunction descriptors. | ||
| theodore_step | integer | Calculate wavefunction descriptors every $1 time step. | |
| 1 | By default calculated every time step (if theodore). | ||
| n_property1d | integer | Allocate for that many 1D properties. | |
| 1 | |||
| n_property2d | integer | Allocate for that many 2D properties. | |
| 1 | |||
| – Output control keywords – | |||
| write_grad | Writes gradients to output.dat. | ||
| nowrite_grad | |||
| write_nacdr | Writes NACs to output.dat. | ||
| nowrite_nacdr | |||
| write_overlap | Writes overlaps to output.dat. | ||
| nowrite_overlap | Not written if not requested. | ||
| write_property1d | on if theodore | Writes 1D properties to output.dat. | |
| nowrite_property1d | |||
| write_property2d | on if ionization | Writes 2D properties to output.dat. | |
| nowrite_property2d | |||
| output_dat_steps | integer | Determines at which steps sharc.x writes to output.dat. | |
| $1 (1) | Stride for writing to output.dat (default every step). | ||
| $2 (not given) | Step at which stride is switched to $3. | ||
| $3 (not given) | New stride applied if step ≥ $2. | ||
| $4 (not given) | Step at which stride is switched to $5. | ||
| $5 (not given) | New stride applied if step ≥ $4. | ||
| Always give 1, 3, or 5 arguments. | |||
| output_format | string | Format of output.dat. | |
| $1=ascii | as documented in section 5.3. | ||
| $1=netcdf | as documented in section 5.4. | ||
| Also deactivates writing of restart files (except last step) and output.xyz. | |||
4.1.3 Detailed Description of the Keywords
Printlevel
The printlevel keyword controls the verbosity of the log file. The data output file (output.dat) and the listing file (output.lis) are not affected by the print level. The print levels are described in section 5.1.
Restart
There are two keywords controlling trajectory restarting. The keyword restart enables restarting, while norestart disables restart. If both keywords are present, norestart takes precedence. The default is no restart.
When restarting, all control variables are read from the restart file instead of the input file. The only exceptions are nsteps and tmax. In this way, a trajectory which ran for the full simulation time can easily be restarted to extend the simulation time.
Note that none of the auxiliary scripts adds the restart keyword to the input file. The user has to manually add the restart file to the input files of the relevant trajectories.
In order to ensure synchronicity of the restart files of sharc.x and the restart/ directory (managed by the interfaces), either one of two keywords must be present when restarting, either restart_rerun_last_qm_step or restart_goto_new_qm_step.
The restart_rerun_last_qm_step keyword should be used if the restart is after a non-graceful crash/kill of the simulation (e.g., due to queueing system time limits).
It tells the interface that the current time step was already attempted before the restart and the restart/ directory is one time step ahead of the information in the restart files.
The restart_goto_new_qm_step keyword on the contrary should be used after the simulation was gracefully stopped (e.g., after reaching tmax/nsteps, after using the STOP file, or after using the killafter mechanism).
In this case, restart files and restart/ directory are consistent and the simulation continues as if no stop-and-restart were performed.
RNG Seed
The RNG seed is used to initialize the random number generator, which provides the random numbers for the surface hopping procedure (and the AFSSH decoherence scheme). For details how the seed is used internally, see section 8.26.
Note that in the case of a restart, the random number generator is seeded normally, and then the appropriate number of random numbers is drawn so that the random number sequence is consistent.
Compatibility Mode
With this keyword, one can activate a compatibility mode that allows reproducing results of older versions of SHARC.
A value of 0 disables compatibility mode.
Currently, the only other option is a value of 1.
In this mode, sharc.x draws only one random number for each step, like it was the case in SHARC 1.0 (from SHARC 2.0, it draws two random numbers per step, one for hopping and one for decoherence schemes).
This compatibility mode cannot be combined with the A-FSSH decoherence correction.
Geometry Input
The initial geometry must be given in a second file in the input format also used by COLUMBUS. The default name for this file is geom. The geometry filename can be given in the input file with the geomfile keyword. Note that the filename has to be enclosed in single or double quotes. See section 4.2 for more details.
Velocity Input
Using the veloc keyword, the initial velocities can be either set to zero, determined randomly or read from a file. Random determination of the velocities is such that each atom has the same kinetic energy, which must be specified after veloc random in units of eV. Determination of the random velocities is detailed in 8.22. Note that after the initial velocities are generated, the RNG is reseeded (i.e., the sequence of random numbers in the surface hopping procedure is independent of whether random initial velocities are used).
Alternatively, the initial velocities can be read from a file.
The default velocity filename is veloc, but the filename can be specified with the velocfile keyword. Note that the filename has to be enclosed in single or double quotes. The file must contain the Cartesian components of the velocity for each atom on a new line, in the same order as in the geomety file. The velocity is interpreted in terms of atomic units (bohr/atu). See section 4.3 for more details.
Number of States and Active States
The keyword nstates controls how many states are taken into account in the dynamics. The keyword arguments specify the number of singlet, doublet, triplet, etc. states. There is no hard-coded maximum multiplicity in the SHARC code, however, some interfaces may restrict the maximum multiplicity.
Using the actstates keyword, the dynamics can be restricted to some lowest states in each multiplicity. For each multiplicity, the number of active states must not be larger than the number of states. All couplings between the active states and the frozen states are deleted. These couplings include off-diagonal elements in the HMCH matrix, in the overlap matrix, and in the matrix containing the nonadiabatic couplings. Freezing states can be useful if transient absorption spectra are to be calculated without increasing computational cost due to the large number of states.
Note that the initial state must not be frozen.
Initial State
The initial state can be given either in MCH or diagonal representation. The keyword state is followed by an integer specifying the initial state and either the string mch or diag. For the MCH representations, states are enumerated according to the canonical state ordering, see 8.28. The diagonal states are ordered according to energy. Note that the initial state must be active.
If the initial state is given in the MCH basis but the dynamics is carried out in the diagonal basis, determination of the initial diagonal state is carried out after the initial QM calculation.
Initial Coefficients
The initial coefficients can be determined automatically from the initial state, using coeff auto in the input file. If the initial state is given in the diagonal representation as i, the initial coefficients are cdiagj=δij. If the initial state is, however, given in the MCH representation, then cMCHj=δij and the determination of cdiag=U†cMCH is carried out after the initial QM calculation.
Currently, coeff auto is always used by the automatic setup scripts.
Besides automatic determination, the initial coefficients can be read from a file. The default filename is coeff, but the filename can be given with the keyword coefffile. Note that the filename has to be enclosed in single or double quotes. The file must contain the real and imaginary part of the initial coefficients, one line per state with no blank lines inbetween. These coefficients are interpreted to be in the same representation as the initial state, i.e. the state keyword influences the initial coefficients. For details on the file format, see section 4.4.
Note that the setup scripts currently cannot setup trajectories with coeff external, so this can be considered an expert option.
Laser Input
The keyword laser controls whether a laser field is included in the dynamics (influencing the coefficient propagation and the energies/gradients by means of the Stark effect).
The input of an external laser field uses the file laser. This file is specified in 4.5.
In order to detect laser-induced hops, SHARC compares the instantaneous central laser energy with the energy gap between the old and new states. If the difference between the laser energy and the energy gap is smaller than the laser bandwidth (given with the laserwidth keyword), the hop is classified as laser-induced. Those hops are never frustrated and the kinetic energy is not scaled to preserve total energy (instead, the kinetic energy is preserved).
Simulation Timestep
The keyword stepsize controls the length of a time step (in fs) for the dynamics. The nuclear motion is integrated using the Velocity-Verlet algorithm with this time step. Surface hopping is performed once per time step and 1-3 quantum chemistry calculations are performed per time step (depending on the selection schedule). Each time step is divided in nsubsteps substeps for the integration of the electronic equation-of-motion. Since integration is performed in the MCH representation, the default of 25 substeps is usually sufficient, even if very small potential couplings are encountered. A larger number of substeps might be necessary if high-frequency laser fields are included or if the energy shift (ezero) is not well-chosen.
Simulation Time
The keyword nsteps controls the total length of the simulation. The total simulation time is nsteps times stepsize. nsteps does not include the initial quantum chemistry calculation. Instead of the number of steps, the total simulation time can be given directly (in fs) using the keyword tmax. In this case, nsteps is calculated as tmax divided by stepsize. If both keywords (nsteps and tmax) are present, nsteps is used. All setup scripts will generally use the tmax keyword.
Using the keyword killafter, the dynamics can be terminated before the full simulation time. killafter specifies (in fs) the time the trajectory can move in the lowest-energy state before the simulation is terminated. By default, simulations always run to the full simulation time and are not terminated prematurely.
Integrator for Nuclear Equation of Motion
The keyword integrator controls the integrator for nuclear equation of motion used in SHARC. There are two options, integrator fvv uses the fixed time step velocity Verlet algorithm, which is the default. The time step in fixed time step velocity Verlet is set by keyword stepsize.
Alternatively, one can use integrator avv, which turns on the adaptive time step velocity Verlet algorithm. The initial time step in adaptive velocity Verlet algorithm is set by keyword stepsize. In adaptive velocity Verlet, the algorithm will check the total energy conservation of the trajectory at successive time steps. If the energy difference is above the threshold, the timestep will be reduced to half, and if the energy difference is less than one fifth of the threshold, the timestep will be doubled. The threshold can be set by keyword convthre, the default is 1e-04 eV. One can also set up the minimum and maximum allowed stepsize in adaptive velocity Verlet. This is achieved by keyword stepsize_min and stepsize_max. The default values for stepsize_min and stepsize_max are stepsize/16 and stepsize*2 respectively. Alternatively, one can set up the minimum or maximum stepsize in an exponential form to base 2. This is done by calling keywords stepsize_min_exp and stepsize_max_exp. The default values for these two keywords are -4 and 1, respectively. For example, when setting stepszie_min_exp -4, the minimum stepsize is stepsize/(2−4). Setting up keywords stepsize_min_exp and stepsize_max_exp will overwrite keywords stepsize_min and stepsize_max.
If the adaptive time step is used, the output files will contain data at the computed times, which might not be a regular grid of time steps. This can lead to a swarm of trajectories that do not have data at the same time steps. To enable ensemble analysis, in this case data_extractor.x will automatically perform linear interpolation of the results. It will write all output files twice, once with the original time steps (file names contain original) and once interpolated to multiples of the original stepsize.
Note that for the SHARC3.0 release, adaptive time steps are not available when the compilation was done with pysharc support.
Dynamics Method
Starting from SHARC3.0, one is able to perform two categories of nonadiabatic dynamics algorithms, namely trajectory surface hopping, and self-consistent potential methods. The dynamics employed can be set up by keyword method. Using keyword method tsh enables trajectory surface hopping, and method scp enables self-consistent potential methods.
Note that for the SHARC3.0 release, self-consistent potential methods are not available when the compilation was done with pysharc support.
Description of Non-adiabatic Coupling
The code allows propagating the electronic wave function using four different quantities describing nonadiabatic effects, see 8.33. The keyword coupling controls which of these quantities is requested from the QM interfaces and used in the propagation. The first option is nacdr, which requires the nonadiabatic coupling vectors 〈ψα|∂/∂R|ψβ〉. For the wave function propagation, the scalar product of these vectors and the nuclear velocity is calculated to obtain the matrix 〈ψα|∂/∂t|ψβ〉. During the propagation, this matrix is interpolated linearly within each classical time step. Currently, only few SHARC interfaces can provide these couplings.
Alternatively, one can directly request the matrix elements 〈ψα|∂/∂t|ψβ〉, which can be used for the propagation. The corresponding argument to coupling is nacdt. In this case, the matrix is taken as constant throughout each classical time step. Currently, none of the interfaces in SHARC can deliver these couplings, because they are computed via overlaps, and if overlaps are known it is preferable to use local diabatization.
The third possibility is the use of the overlap matrix, requested with coupling overlaps (this is the default). The overlap matrix is used subsequently in the local diabatization algorithm for the wave function propagation. Currently, all SHARC interfaces can provide these couplings.
The fourth possibility is to use the curvature driven method to approximate time derivative couplings (coupling ktdc). In curvature driven methods, the time derivative coupling is completely approximated by knowing the curvatures of the potential energy surfaces. And therefore, can be interfaced with electronic structure theories for which the nonadiabatic coupling vector is not available, or the wave function is not defined – and therefore one can not compute overlap integrals from electronic structure theory. Therefore, curvature driven methods can be interfaced with any electronic structure theory that provides energies and gradients.
Method to Compute Curvature Approximated Time Derivative Coupling
If one uses coupling ktdc, there are two possible ways to compute time derivative coupling (TDC). One can compute the curvature of potential energy surface with respect to time from either the second order finite difference of energy along time by calling ktdc_method energy; or from the first order finite difference of the dot product of gradients and velocity vector ktdc_method gradient, see 8.34.
Electronic Equation of Motion Propagator
One can control the electronic propagator by calling keyword eeom, see 8.33. There are four options, eeom ci does not interpolate the time derivative coupling during the substep propagation. eeom li linearly interpolates the time derivative coupling during the substep propagation. eeom ld uses the local diabatization. eeom npi uses a norm preserving interpolation propagator.[115,[93] We suggest the users use the default propagator, which depends on the used coupling quantity.
Correction to the Diagonal Gradients
As detailed in 8.11, transformation of the diagonal representation requires contributions from the nonadiabatic coupling vectors or time derivative couplings. The two correction schemes are called nuclear-gradient-tensor scheme and time-derivative-matrix scheme. The nuclear-gradient-tensor scheme corrects the gradients with nonadiabatic coupling vectors. In this case SHARC will request the calculation of the nonadiabatic coupling vectors, even if they are not used in the wave function propagation. The time-derivative-matrix scheme corrects the gradients with the time derivative couplings. Using gradcorrect, gradcorrect ngt, or gradcorrect nac enables nuclear-gradient-tensor scheme; using gradcorrect tdm enables time-derivative-matrix scheme. In order to explicitly turn off this gradient correction, use the nogradcorrect keyword.
Method to Compute Time-Derivative-Matrix Scheme
This approach only applies when one uses gradcorrect tdm. There are two ways to compute time derivatives of potential energies in the diagonal basis in the TDM scheme. One can compute the time derivative of potential energies in the diagonal basis from transformation of the time derivative matrix in the MCH basis. This computation is enabled by using tmd_method gradient. In this approach, the time derivative of potential energies in the MCH basis are computed from the dot product between the nuclear gradient vector and the velocity vector. This is the default option for coupling ddr or coupling overlap.
Alternatively, one can compute the time derivative of potential energies in the diagonal basis from finite differences. This approach is more accurate for curvature driven methods because in curvature-driven algorithms we do not have ab initio time derivative couplings. This is the default option for coupling ktdc
Decoherence Correction Scheme
There are four options for the decoherence correction (see 8.7) in SHARC, which can be selected with the decoherence_scheme keyword.
With the default decoherence_scheme none, no decoherence correction is applied.
The energy-difference based decoherence (EDC) scheme of Granucci et al. [116] can be activated with decoherence_scheme edc.
The keyword decoherence_param can be used to change the relevant parameter α (see 8.7). The default is 0.1 Hartree, which is the value recommended by Granucci et al. [116]. Notice EDC scheme only applies to TSH methods.
Alternatively, the AFSSH (augmented fewest-switches surface hopping) scheme of Jain et al. [30] can be employed, using decoherence_scheme afssh. This scheme does not use any parameters, so the keyword decoherence_param will have no effect.
Note that in any case, the decoherence correction is applied to the states in the representation chosen with the surf keyword.
For self-consistent potential methods, the decay of mixing decoherence scheme of Truhlar et al.[118,[91,[92] can be activated with decoherence_scheme dom. In combination with method scp, it enables either CSDM or SCDM methods. The decoherence time in CSDM or SCDM uses energy based decoherence time. The keywords decoherence_param_alpha and decoherence_param_beta can be used to change the relevant parameters α and β (see 8.7). The default is 0.1 Hartree for α and 1 for β.
Note that for the SHARC3.0 release, self-consistent potential methods and decay of mixing decoherence are not available when the compilation was done with pysharc support.
The keywords decoherence (activates EDC decoherence) and nodecoherence are present for backwards compatibility.
Surface Treatment
The keyword surf controls whether the dynamics runs on diagonal potential energy surfaces (which makes it a SHARC simulation) or on the MCH PESs (which corresponds to a spin-diabatic [26] or FISH [25] simulation, or a regular surface hopping simulation). Internally, dynamics on the MCH potentials is conducted by setting the U matrix equal to the unity matrix at each time step.
Adjustment of the Kinetic Energy
The keyword ekincorrect controls how the kinetic energy is adjusted after a surface hop to preserve total energy. ekincorrect none deactivates the adjustment, so that the total energy is not preserved after a hop. Using this option, jumps can never be frustrated and are always performed according to the hopping probabilities.
Using ekincorrect parallel_vel, the kinetic energy is adjusted by simply rescaling the nuclear velocities so that the new kinetic energy is Etot−Epot. Jumps are frustrated if the new potential energy would exceed the total energy.
Using ekincorrect parallel_nac, the kinetic energy is adjusted by rescaling the component of the nuclear velocities parallel to the nonadiabatic coupling vector between the old and new state. The hop is frustrated if there is not enough kinetic energy in this direction to conserve total energy. Note that ekincorrect parallel_nac implies the calculation of the nonadiabatic coupling vector, even if they are not used for the wave function propagation.
Note that using the nonadiabatic coupling vector causes non-conservation of nuclear orbital angular momentum, and center of mass motion.
Using ekincorrect parallel_diff, the kinetic energy is adjusted by rescaling the component of the nuclear velocities parallel to the difference gradient vector between the old and new state. The hop is frustrated if there is not enough kinetic energy in this direction to conserve total energy.
Using ekincorrect parallel_pnac, the kinetic energy is adjusted by rescaling the component of the nuclear velocities parallel to the projected nonadiabatic coupling vector between the old and new state. The hop is frustrated if there is not enough kinetic energy in this direction to conserve total energy. Projected nonadiabatic coupling vector ensures conservation of nuclear orbital angular momentum and center of mass motion.
Using ekincorrect parallel_enac, the kinetic energy is adjusted by rescaling the component of the nuclear velocities parallel to the effective nonadiabatic coupling vector between the old and new state. The hop is frustrated if there is not enough kinetic energy in this direction to conserve total energy. Notice that effective nonadiabatic coupling vector also destroys the conservation of nuclear orbital angular momentum and center of mass motion.
Using ekincorrect parallel_penac, the kinetic energy is adjusted by rescaling the component of the nuclear velocities parallel to the projected effective nonadiabatic coupling vector between the old and new state. The hop is frustrated if there is not enough kinetic energy in this direction to conserve total energy. Using the projection conserves angular momentum and center of mass motion.
Frustrated Hops
The keyword reflect_frustrated furthermore controls whether the velocities are inverted after a frustrated hop.
With reflect_frustrated none (the default), after a frustrated hop, the velocity vector is not modified.
Using reflect_frustrated parallel_vel, the full velocity vector is inverted when a frustrated hop is encountered.
With the third option, reflect_frustrated parallel_nac, only the velocity component parallel to the nonadiabatic coupling vector between the active and frustrated states is inverted. This implies the calculation of the nonadiabatic coupling vector, even if they are not used for the wave function propagation. Note that reflect the velocity along the direction of nonadiabatic coupling vector will cause non-conservation of nuclear orbital angular momentum and center of mass motion.
With reflect_frustrated parallel_diff, only the velocity component parallel to the gradient difference vector between the active and frustrated states is inverted.
With reflect_frustrated parallel_pnac, only the velocity component parallel to the projected nonadiabatic coupling vector between the active and frustrated states is inverted. Using projection operator conserves nuclear orbital angular momentum and center of mass motion.
With reflect_frustrated parallel_enac, only the velocity component parallel to the effective nonadiabatic coupling vector between the active and frustrated states is inverted.
With reflect_frustrated parallel_penac, only the velocity component parallel to the projected effective nonadiabatic coupling vector between the active and frustrated states is inverted. Using projected effective nonadiabatic coupling vector ensures conservation of angular momentum.
Alternatively, one can employ the ∇V criteria by Jasper and Truhlar.[117] This is enabled by calling respectively reflect_frustrated delV_vel, reflect_frustrated delV_pvel, reflect_frusrated delV_nac, reflect_frustrated delV_diff, reflect_frustrated delV_pnac, reflect_frustrated delV_enac, and reflect_frustrated delV_penac for velocity component parallel to velocity vector, projected velocity vector, nonadiabatic coupling vector, gradient difference, projected nonadiabatic coupling vector, efffective nonadiabatic coupling vector, and projected effective nonadiabatic coupling vector.
Surface Hopping Scheme
There are three options for the computation of the hopping probabilities (see 8.29) in SHARC, which can be selected with the hopping_procedure keyword.
Using hopping_procedure off, surface hopping will be disabled, such that the active state (in the representation chosen with the surf keyword) will never change.
With the default, hopping_procedure sharc, the standard hopping probability equation from Ref. [42] will be used.
Alternatively, one can use the global flux surface hopping scheme [71], which might be advantageous in super-exchange situations.
One can also turn off surface hopping with the no_hops keyword.
Surface hopping with time uncertainty
The time uncertainty algorithm is the same as the Tully’s fewest switches algorithm except when a frustrated hop is encountered.[98,[97] When a frustrated hop is encountered, the trajectory surface hopping with fewest switches and time uncertainty (TSH-FSTU) method effectively looks for nearby regions where a hop can be successful. Then, if a such a region is found, the TSH-FSTU method allows a nonlocal hop. One can interpret this as the FSTU algorithm borrowing some energy along the timeline of the trajectory according to time-energy uncertainty principle. The FSTU algorithm can greatly reduce the number of frustrated hops. The time uncertainty option can be turn on by using keyword time_uncertainty
Note that for the SHARC3.0 release, surface hopping with time uncertainty is not available when the compilation was done with pysharc support.
Forced Hops to Ground State
With this option, one can force SHARC to hop from the active to the lowest state if the energy gap between these two states falls below a certain threshold.
The threshold is given as argument to the force_hop_to_gs keyword (in eV).
This option is useful for single-reference methods that fail to converge if the ground state-excited state energy gap becomes too small.
c
Note that this option forces hops from any higher-lying state to the lowest, independent whether there are other states between the active and the lowest state.
Also note that once in the lowest state, hopping is completely forbidden if this option is active.
Atom Masking
Some of the above surface hopping settings might not be fully size consistent: (i) in ekincorrect parallel_vel, all atoms are uniformly accelerated/slowed during velocity rescaling; (ii) in reflect_frustrated parallel_vel, the velocities of all atoms are inverted; (iii) with decoherence_scheme edc, the kinetic energy of all atoms determines the decoherence rate. In large systems (e.g., in solution), these effects might be unrealistic, because, e.g., a surface hop in the chromophore should not uniformly slow down all water molecules.
The atommask keyword can then be used to exclude certain atoms from the three mentioned procedures. With atommask external, the list of masked and active atoms is read from the file specified with the atommaskfile keyword (default ätommask"). The format of this file is described in section 4.6. With the other possible option, atommask none (the default), all atoms are considered for these procedures.
Note that the atommask keyword has no effect on ekincorrect parallel_nac, reflect_frustrated parallel_nac, and decoherence_scheme afssh, because these procedures are size consistent by themselves.
Noandiabatic Force Direction in SCP Methods
In generalized self-consistent potential method, the nuclear equation of motion involves two terms, the adiabatic force and nonadiabatic force, see 8.30. The keyword neom controls the direction of the nonadiabatic force. There are two options, neom ddr or neom nacdr uses the nonadiabatic coupling vector as the direction for nonadiabatic force. This reduces the generalized semiclassical Ehrenfest to original semiclassical Ehrenfest. Alternatively, one can use neom gdiff where the direction of nonadiabatic force is set to be effective nonadiabatic coupling vector, see 8.31.
Projection Operator that Removes Artificial Translational and Rotational Motions
If one uses nonadiabatic coupling vector or effective nonadiabatic coupling vector as a direction of nonadiabatic force in SCP methods, one will encounter non-conservation of nuclear orbital angular momentum and center of mass motion. Therefore, it is highly suggested (and as default) that one should perform projection on nonadiabatic coupling vector and effective nonadiabatic coupling vector.[95] The projection operator removes the translational and rotational components of a vector. Therefore, using nac_projection conserves nuclear orbital angular momentum and center of mass motion.
Pointer Basis
The keyword pointer_basis controls the representation of the pointer state in the decay of mixing algorithm (self-consistent potential method),[94] i.e., whether decoherence converges towards a state in the diagonal basis or MCH basis. It is recommended to use the diagonal representation by setting pointer_basis diag, and this is the default option.
Surface Switching Procedure
Keyword switching_procedure only applies to self-consistent potential methods. This keyword controls how pointer state is switched in decay of mixing algorithms. switching_procedure csdm turns on coherent switching with decay of mixing (CSDM). In CSDM switching procedure, one propagates two populations, namely true electronic population which involves decay of mixing, and coherent electronic population which only propagates coherently. The coherent population will be synchronized to the true electronic population for every complete passage of a strong interaction region. This procedure has been shown to be the most accurate way to compute pointer state switching probability.[91,[119]
Alternatively, one can use an older version of decay of mixing algorithm called self-consistent decay of mixing (SCDM), which can be enabled by using switching_procedure scdm. Similarly as in CSDM, one propagates both true electronic population and coherent electronic population. The difference between CSDM and SCDM is that in SCDM one does not synchronize the coherent electronic population to true population. This has been shown to be accurate in many cases but not as accurate as CSDM.
Decoherence Parameters for Decay of Mixing Algorithms
Similarly as in EDC, decay of mixing uses an energy-based decoherence time.[118,[91] Two parameters in energy-based decoherence time can be changed, see 8.7. The two parameters can be set by keywords decoherence_param_alpha and decoherence_param_beta. Default values for these two parameters are 0.1 Hartree and 1.0. These are also the suggested values in the original publicaton.[91]
NAC projection
When using NACs computed from electronic structure software in nuclear equation of motion of the SCP method, it does not preserve conservation of angular momentum and center of mass motion. The projection operator option (nac_projection) removes translational and rotational components in a vector. Therefore, it is suggested that one should always use projected NACs or projected effective NACs in nuclear EOM.
The keywords nac_projection and nonac_projection are used to control if the projection should be used for terms involve NACs in SCP methods. If nac_projection is used, then the nonadiabatic force direction in SCP methods set by keyword neom will be projected. Therefore, using nac_projection is always suggested and is set to default.
For trajectory surface hopping, the only place that may exist a term associated with NACs are in momendum adjustment after a hop or momentum reversal after a frustrated hop. Using projected velocity vector, projected NACs or projected effective NACs can be set up using the keywords ekincorrect and reflect_frustrated.
Bond length constraints with RATTLE
One can use the RATTLE algorithm to constrain the length of some bonds (or generally, interatomic distances) to some fixed value.
The rattle keyword can be used to activate this option.
Activating rattle requires providing a file with the list of atom pairs whose distance should be fixed.
The format for this file is described in section 4.7.
One can also use the rattletolerance keyword to modify the convergence criterion of the RATTLE linear equation solver.
However, for most purposes, the default should be acceptable.
Reference Energy
The keyword ezero gives the energy shift for the diagonal elements of the Hamiltonian. The shift should be chosen so that the shifted diagonal elements are reasonably small (large diagonal elements in the Hamiltonian lead to rapidly changing coefficients, requiring extremely short subtime steps).
Note that the energy shift default is 0, i.e., SHARC does not choose an energy shift based on the energies at the first time step (this would lead to each trajectory having a different energy shift).
Scaling and Damping
The scaling factor for the energies and gradients must be positive (not zero), see section 8.25.
One can also scale only spin-orbit couplings by using soc_scaling.
The damping factor must be in the interval [0,1] (first, since the kinetic energy is always positive; second, because a damping factor larger than 1 would lead to exponentially growing kinetic energy). Also see section 8.6.
Selection of Gradients and Non-Adiabatic Couplings
SHARC allows to selectively calculate only certain gradients and nonadiabatic coupling vectors at each time step. Those gradients and nonadiabatic coupling vectors not selected are not requested from the interfaces, thus decreasing the computational cost. The selection procedure is detailed in 8.27.
Selection of gradients is activated by grad_select, selection for nonadiabatic couplings by nac_select. Selection is turned off by default.
The selection procedure picks only states which are closer in energy to the classically occupied state than a given threshold. The threshold is 0.5 eV by default and can be adjusted using the eselect keyword.
Since SHARC2.1, by default the select_directly keyword is active, which tells SHARC to use the energies of the last time step for selecting, so that only one call per time step is necessary.
The alternative (keyword noselect_directly) is to perform two quantum chemistry calls per time step. In the first call, all quantities are requested except for the ones to be selected. The energies are used to determine which gradients and NACs to calculate in a second quantum chemistry call.
The option select_directly is strongly recommended in almost all instances, since for most quantum chemistry programs it is not possible to make sure that the wave function phases from both calls are consistent.
Additionally, for all interfaces the calculation becomes more expensive with two calls per step.
Note that some interface may (for some electronic structure methods) compute the gradients numerically.
In this case, the interface will automatically compute the gradients of all states together.
Therefore, grad_select offers no advantage for numerical gradient runs and it is strongly suggested to use the default option grad_all.
Phase Tracking
Phase tracking is an important ingredient in SHARC. It is necessary for two reasons: (i) the columns of the transformation matrix U are determined only up to an arbitrary phase factor eiϕ (and additional mixing angles in case of degeneracy), and (ii) the wave functions produced by any quantum chemistry code are determined only up to an arbitrary sign.
Both kind of phases need to be tracked in SHARC in order to obtain smoothly varying matrix elements which can be properly integrated.
By default, SHARC automatically tracks the phases in the U matrix (explicit keyword: track_phase), because all required information is always available. This phase tracking can be deactivated with the notrack_phase keyword, which can provide a significant speed advantage for pysharc calculations. However, you should check whether your results are affected by notrack_phase, and revert to track_phase if they do.
The tracking of the wave function signs depends on the interfaces, because only they have access to the explicit form of the wave functions. SHARC by default (explicit keyword: phases_from_interface) requests that the interface tracks the signs and reports any sign changes to SHARC. Currently, all interfaces can provide this phase information, but all of them need to perform overlap calculations to do so. The nophases_from_interface keyword can be used to deactivate these requests.
In some situations, it might be necessary to have consistent wave function signs between different trajectories. In this case, the phases_at_zero keyword can be used to compute sign information at t=0; this requires that the relevant wave function data of the reference is already located in the restart/ directory before the trajectory is started. Note that phases_at_zero is therefore an expert option.
Spin-Orbit Couplings
Using the keyword nospinorbit the calculation of spin-orbit couplings is disabled. SHARC will only request the diagonal elements of the Hamiltonian from the interfaces. If the interface returns a non-diagonal Hamiltonian anyways, the off-diagonal elements are deleted.
The keyword spinorbit (which is the default) enables spin-orbit couplings.
Dipole Moment Gradients
The derivatives of the dipole moments can be included in the gradients. This can be activated with the keyword dipole_gradient. Currently, only the analytical and MOLCAS interfaces can deliver these quantities.
Ionization
The keyword ionization activates (noionization deactivates) the on-the-fly calculation of ionization transition properties. If the keyword is given, by default these properties are calculated every time step. The keyword ionization_step can be used to calculate these properties only every n-th time step.
If the keyword is given, SHARC will request the calculation of the ionization properties from the interface, which needs to be able to calculate them.
The ionization probabilities are treated as one 2D property matrix, hence n_property2d should be at least 1.
THEODORE
The keyword theodore activates (notheodore deactivates) the on-the-fly calculation of wave function descriptors with the THEODORE program. This can be very useful to track the wave function character of the states on-the-fly.
The interface must be able to execute and THEODORE and return its output to SHARC (currently, the ADF, GAUSSIAN, TURBOMOLE, and ORCA interfaces can do this). The keyword theodore_step can be used to calculate these descriptors only every n-th time step.
The THEODORE descriptors are treated as one 1D property vector for each descriptor, and n_property1d should be at least as large as the number of descriptors computed by the interface.
Output control
There are a number of keywords which control what information is written to the output.dat file.
These keywords are write_grad, write_nacdr, write_overlap, write_property1d, and write_property2d (and the inverse of each one, e.g., nowrite_grad).
Only write_overlap is activated by default, because it does not enlarge the data file by much, and contains important information which is read by data_extractor.x.
write_grad and write_nacdr are turned off by default; they are primarily intended for users who want to keep all quantum chemical data, e.g., for training in machine learning.
The keywords write_property1d and write_property2d are automatically activated if theodore or ionization (respectively) are activated.
Output writing stride
The keyword output_dat_steps can be used to control how often data is written to output.dat.
This is useful to reduce the amount of data generated by long trajectories (e.g., with the LVC or Analytical interfaces).
In the simplest version, using output_dat_steps N will set the output stride to N, so that output.dat is updated every N-th step (i.e., if step modulo N is equal to zero).
The default is to write every step.
Because in nonadiabatic dynamics, usually ballistic processes occur rapidly in the beginning and statistical processes occur slowly for longer times, this keyword allows printing more often in the beginning and less often for longer times.
To use this feature, write output_dat_steps N1 M2 N2, which will use N1 as the stride if step is larger or equal to zero, and N2 as the stride if step is larger or equal to M2.
One can also use three different strides via output_dat_steps N1 M2 N2 M3 N3, but not more than three.
Note that for these numbers sharc.x enforces N ≥ 1 and M ≥ 0, but no particular ordering.
Hence, it is possible to use longer strides in the beginning and smaller strides later, although this is rarely useful.
If step is larger/equal to both M2 and M3, then N3 will be used.
Also note that the data written to output.dat is always simply the data for the respective time step, no average over the last N steps.
This needs to be kept in mind when analyzing the trajectory plots.
Setting a variable output stride is currrently not compatible with the adaptive time step integrator.
Output format
See sections 5.3 and 5.4 for details.
4.1.4 Example
The following input sample shows a typical input for excited-state dynamics including IC within a singlet manifold plus intersystem crossing to triplet states. It includes a large number of excited singlet states in order to calculate transient absorption spectra. Only the lowest three singlet states actually participate in the dynamics.
nstates 8 0 3 # many singlet states for transient absorption actstates 3 0 3 # only few states to reduce gradient costs stepsize 0.5 # typical time step for a molecule containing H tmax 1000.0 # one picosecond surf diagonal state 3 mch # start on the S2 singlet state coeff auto # coefficient of S2 will be set to one coupling overlap # \ decoherence_scheme edc # | typical settings ekincorrect parallel_vel # | gradcorrect # / grad_select # \ nac_select # | improve performance eselect 0.3 # / veloc external # velocities come from file "veloc" velocfile "veloc" # RNGseed 65435 ezero -399.41494751 # ground state energy of molecule
4.2 Geometry file
The geometry file (default file name is geom) contains the initial coordinates of all atoms. This file must be present when starting a new trajectory.
The format is based on the COLUMBUS geometry file format (however, SHARC is more flexible with the formatting of the numbers). For each atom, the file contains one line, giving the chemical symbol (a string), the atomic number (a real number), the x, y and z coordinates of the atom in Bohrs (three real numbers), and the relative atomic weight of the atom (a real number). The six items must be separated by spaces. The real numbers are read in using Fortran list-directed I/O, and hence are free format (can have any numbers of decimals, exponential notation, etc.). Element symbols can have at most 2 characters.
The following is an example of a geom file for CH2:
C 6.0 0.0 0.0 0.0 12.000 H 1.0 1.7 0.0 -1.2 1.008 H 1.0 1.7 0.0 3.7 1.008
4.3 Velocity file
The velocity file (default veloc) contains the initial nuclear velocities (e.g., from a Wigner distribution sampling). This file is optional (the velocities can be initialized with the veloc input keyword).
The file contains one line of input for each atom, where the order of atoms must be the same as in the geom file. Each line consists of three items, separated by spaces, where the first is the x component of the nuclear velocity, followed by the y and z components (three real numbers). The input is interpreted in atomic units (Bohr/atu).
The following is an example of a veloc file:
0.0001 0.0000 0.0002 0.0002 0.0000 0.0012 0.0003 0.0000 -0.0007
4.4 Coefficient file
The coefficient file contains the initial wave function coefficients. The file contains one line per state (total number of states, i.e., multiplets count multiple times). Each line specifies the initial coefficient of one state. If the initial state is specified in the MCH representation (input keyword state), then the order of the initial coefficients must be as given by the canonical ordering (see section 8.28). If the initial state is given in diagonal representation, then the initial coefficients correspond to the states given in energetic ordering, starting with the lowest state.
Each line contains two real numbers, giving first the real and then the imaginary part of the initial coefficient of the respective state.
Note that after read-in, the coefficient vector is normalized to one.
Example:
0.0 0.0 1.0 0.0 0.0 0.0
4.5 Laser file
The laser file contains a table with the amplitude of the laser field ϵ(t) at each time step of the electronic propagation. Given a laser field of the general form:
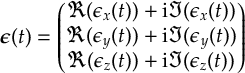 |
(4.1) |
each line consists of 8 elements: t (in fs), ℜ(ϵx(t)), ℑ(ϵx(t)), ℜ(ϵy(t)), ℑ(ϵy(t)), ℜ(ϵz(t)), ℑ(ϵz(t)), (all in atomic units), and finally the instantaneous central frequency (also atomic units).
The time step in the laser file must exactly match the time step used for the electronic propagation, which is the time step used for the nuclear propagation (keyword stepsize) divided by the number of substeps (keyword nsubsteps). The first line of the laser file must correspond to t=0 fs.
Example:
0.00E+00 -0.68E-03 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.31E+00 0.10E-02 -0.77E-02 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.33E+00 0.20E-02 -0.13E-01 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.35E+00 ... ... ... ... ... ... ... ...
4.6 Atom mask file
The atom mask file contains for each atom a line with a Boolean entry (“T” or “F”), which indicates whether the atom should be considered in the relevant procedures. Specifically, the atom masking settings affect the options ekincorrect parallel_vel, reflect_frustrated parallel_vel, and decoherence_scheme edc.
In all cases, “T” indicates that the atom should be considered (as if atommask was not given), whereas “F” indicates that the atom should be ignored for these procedures.
Example:
T T F F ...
4.7 RATTLE file
The RATTLE file contains a list of all the atom pairs whose interatomic distance should be fixed by the RATTLE algorithm.
In the file, each line should contain two integer numbers that indicate the atom indices of one atom pair.
Atom indices start at 1.
Optionally, some lines can also have a third entry, which is a float with the desired interatomic distance in Bohr units.
If the third entry is not give, then the distance is fixed to the value that is found in the initial geometry file.
Example:
1 3 2 4 2.05 2 5
Chapter 5
Output files
This chapter documents the content of the output files of SHARC. Those output files are output.log, output.lis, output.dat and output.xyz.
5.1 Log file
The log file output.log contains general information about all steps of the SHARC simulation, e.g., about the parsing of the input files, results of quantum chemistry calls, internal matrices and vectors, etc. The content of the log file can be controlled with the keyword printlevel in the SHARC main input file.
In the following, all printlevels are explained.
Printlevel 0
At printlevel 0, only the execution infos (date, host and working directory at execution start) and build infos (compiler, compile date, building host and working directory) are given.
Printlevel 1
At printlevel 1, also the content of the input file (cleaned of comments and blank lines) is echoed in the log file. Also, the start of each time step is given.
Printlevel 2
At printlevel 2, the log file also contains information about the parsing of the input files (echoing all enabled options, initial geometry, velocity and coefficients, etc.) and about the initialization of the coefficients after the first quantum chemistry calculation. This printlevel is recommended for production calculations, since it is the highest printlevel where no output per time step is written to the log file.
Printlevel 3
This and higher printlevels add output per time step to the log file. At printlevel 3, the log file contains at each time step the data from the velocity-Verlet algorithm (old and new acceleration, velocity and geometry), the old and new coefficients, the surface hopping probabilities and random number, the occupancies before and after decoherence correction as well as the kinetic, potential and total energies.
Printlevel 4
At printlevel 4, additionally the log file contains information on the quantum chemistry calls (file names, which quantities were read, gradient and nonadiabatic coupling vector selection) and the propagator matrix.
Printlevel 5
At printlevel 5, additionally the log file contains the results of each quantum chemistry calls (all matrices and vectors), all matrices involved in the propagation as well as the matrices involved in the gradient transformation. This is the highest printlevel currently implemented.
5.2 Listing file
The listing file output.lis is a tabular summary of the progress of the dynamics simulation. At the end of each time step (including the initial time step), one line with 11 elements is printed. These are, from left to right:
- current step (counting starts at zero for the initial step),
- current simulation time (fs),
- current state in the diagonal representation,
- approximate corresponding MCH state (see subsection 8.23.1),
- kinetic energy (eV),
- potential energy (eV),
- total energy (eV),
- current gradient norm (in eV/Å),
- current expectation values of the state dipole moment (Debye),
- current expectation values of total spin,
- wallclock time needed for the time step.
The listing file also contains one extra line for each surface hopping event. For accepted hops, the old and new states (in diagonal representation) and the random number are given. Frustrated hops and resonant hops are also mentioned. Note that the extra line for surface hopping occurs before the regular line for the time step.
The listing file can be plotted with standard tools like GNUPLOT and can be read with data_collector.py.
Energies
The kinetic energy is calculated at the end of each time step (i.e., after surface hopping events and the corresponding adjustments). The potential energy is the energy of the currently active diagonal state. The total energy is the sum of those two.
Expectation values
The gradient norms given in the listing file is calculated as follows:
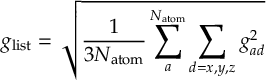 |
(5.1) |
which is then transformed to eV/Å.
The expectation values of the dipole moment for the active state β is calculated from:
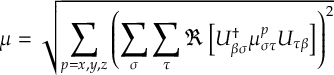 |
(5.2) |
The expectation value of the total spin of the active state β is calculated as follows:
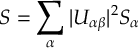 |
(5.3) |
where Sα is the total spin of the MCH state with index α.
5.3 Data file
The data file output.dat contains all relevant data from the simulation for all time steps, in ASCII format. Accordingly, this file can become quite large for long trajectories or if many states are included, but for most file systems it is easier to deal with a single large file than with many small files.
Usually, after the simulation is finished the data file is processed by data_extractor.x to obtain a number of tabular files which can be plotted or post-processed (e.g., with data_collector.py). For this, see sections 7.29 for the data extractor, 7.14 for plotting, and 7.25 for post-processing.
5.3.1 Specification of the data file
The data file format was changed from the first release version of SHARC. The new format uses a different header, which is keyword-based (like the input file) and starts with SHARC_version 2.0. The general structure of the time step data is the same as in the first release version.
The data file contains a short header followed by the data per time step. All quantities are commented in the data file.
The header is keyword-based and contains at least the following entries:
- number of states per multiplicity,
- number of atoms,
- number of 1D properties,
- number of 2D properties,
- time step,
- write_overlap,
- write_grad,
- write_nacdr,
- write_property1d,
- write_property2d,
- information whether a laser field is included.
At the end of the header, the data file contains a header array section. Currently, this includes:
- atomic numbers,
- elements,
- masses,
- full laser field for all substeps (only if flag is set).
The entry for each time step contains:
- step index
- Hamiltonian in MCH representation,
- transformation matrix U,
- MCH dipole moment matrices (x, y, z),
- overlap matrix in MCH representation (only if flag is set),
- coefficients in the diagonal representation,
- hopping probablities in the diagonal representation
- kinetic energy,
- currently active state in diagonal representation and approximate state in MCH representation,
- random number for surface hopping,
- wallclock time (in seconds)
- geometry (Bohrs),
- velocities (atomic units),
- 2D property matrices (only if flag is set),
- 1D property vectors (only if flag is set),
- gradient vectors (only if flag is set),
- nonadiabatic coupling vectors (only if flag is set).
5.4 Data file in NetCDF format
If output_format is set to netcdf, then only the header will be written to the output.dat file, but no information per time step.
The latter is instead written in (binary) NetCDF format to output.dat.nc.
This option is intended to provide faster output for fast simulations with pysharc.
However, it is also an option that leads to less disk memory consumption, and can be used with sharc.x.
To this end, output_format=netcdf also deactivates writing of the output.xyz file.
Also, when NetCDF files are written, no restart files are produced, except on the last time step or in case of errors.
NetCDF output files can be extracted with data_extractor_NetCDF.x (see section 7.12).
This program can also generate the output.xyz for further analysis.
Currently, there are a few limitations in this approach.
Most importantly, the NetCDF files do not store the property vectors and property matrices that can be stored in the output.dat files.
Hence, computations with the ionization or theodore keywords should not use the NetCDF format.
The program data_converter.x (see section 7.13) can be used to convert a output.dat file into a NetCDF file.
This can be useful when archiving an ensemble of trajectories, as the NetCDF files are much smaller than the ASCII files.
Note that after conversion, the output.xyz files can be deleted, as they can be regenerated from the NetCDF file.
5.5 XYZ file
The file output.xyz contains the geometries of all time steps in standard xyz file format. It can be used with visualization programs like MOLDEN, GABEDIT or MOLEKEL to create movies of the molecular motion, or with geo.py (see 7.22) to calculate internal coordinates for each time step. Furthermore, trajana_nma.py (see 7.24) and trajana_essdyn.py (see 7.23) read this file.
The comments of the geometries (given in the second line of each geometry block) contain information about the simulation time and the active state (first in diagonal basis, then in MCH basis).
If output_format=netcdf, the output.xyz file will be empty.
Use data_extractor_NetCDF.x with the -xyz flag to obtain the output.xyz file.
Chapter 6
Interfaces
This chapter describes the interface between SHARC and quantum chemistry programs. In the first section, the interface is specified (e.g., for users who attempt to create their own interfaces). The description of the currently existing interfaces takes the remainder of this chapter.
6.1 Interface Specifications
From the SHARC point of view, quantum chemical calculation proceeds as follows in the QM directory:
- write a file called QM/QM.in
- call a script called QM/runQM.sh
- read the output from a file called QM/QM.out
For specifications of the formats of these two files (QM.in and QM.out) see below. The executable script QM/runQM.sh must accomplish that all necessary quantum chemical output is available in QM/QM.out.
6.1.1 QM.in Specification
The QM.in file is written by SHARC every time a quantum chemistry calculation is necessary. It contains all information available to SHARC. This information includes the current geometry (and velocity), the time step, the number of states, the time step and the unit used to specify the atomic coordinates. The file also contains control keywords and request keywords.
The file format is consistent with a standard xyz file. The first line contains the number of atoms, the second line is a comment. SHARC writes the trajectory ID (a hash of all SHARC input files) to this line. The following lines specify the atom positions. As a fourth, fifth and sixth column, these lines may contain the atomic velocities.
All following lines contain keywords, one per line and possibly with arguments. Comments can be inserted with ‘#’, and empty lines are permitted. Comments and empty lines are only permitted below the xyz file part.
An examplary QM.in file is given in the following:
3 Jobname S 0.0 0.0 0.0 0.000 -0.020 0.002 H 0.0 0.9 1.2 0.000 -0.030 0.000 H 0.0 -0.9 1.2 0.000 0.010 -0.000 # This is a comment Init States 3 0 2 Unit Angstrom SOC DM GRAD 1 2 OVERLAP NACDR select 1 2 end
There exist two types of keywords, control keywords and request keywords. Control keywords pass some information to the interface. Request keywords tell the interface to provide a quantity in the QM.out file. Table 6.1 contains all control keywords while table 6.2 lists all request keywords.
| Keyword | Description |
| init | Specifies that this is the first calculation. The interface should create a save directory (if not existing already) to save all information necessary for a restart. |
| samestep | Specifies that this is an additional calculation at the same geometry/time step. Implies that, e.g., the converged orbitals from the savedir could be reused or that the wave function calculations could be skipped. |
| restart | Specifies that this is a calculation after a restart of sharc.x, possibly after a crash. Implies that in the savedir some files might be incomplete, the interface should therefore act as if a new step is requested, except that the savedir files should be managed accordingly. |
| cleanup | Specifies that all output files of the interface (except QM.out) should be deleted (including the save directory). |
| backup | Specifies that the content of the save directory should be stored in a persistent location (such that it is not overwritten in the next time step). |
| unit | Specifies in which unit the atomic coordinates are to be interpreted. Possible arguments are “angstrom” and “bohr”. |
| states | Gives the number of excited states per multiplicity (singlets, doublet, triplets, …). |
| dt | Gives the time between the last calculation and the current calculation in atomic units. |
| savedir | Gives a path to the directory where the interface should save files needed for restart and between time steps. If the interface-specific input files also have this keyword, SHARC assumes that the path in QM.in takes precedence. |
| Keyword | Description |
| H | Calculate the molecular Hamiltonian (diagonal matrix with the energies of the states of the model space). This request is always available. |
| SOC | Calculate the molecular Hamiltonian including the SOCs (not diagonal anymore within the model space). |
| DM | Calculate the state dipole moments and transition dipole moments between all states. |
| GRAD | Calculate gradients for all states. If followed by a list of states, calculate only gradients for the specified states. |
| NACDT | Calculate the time-derivatives 〈Ψ1|∂/∂t|Ψ2〉 by finite differences between the last time step and the current time step. This request is currently not supported by any interface. |
| NACDR | Calculate nonadiabatic coupling vectors 〈Ψ1|∂/∂R|Ψ2〉 between all pairs of states. If followed by “select”, read the list of pairs on the following lines until “end” and calculate nonadiabatic coupling vectors between the specified pairs of states. |
| OVERLAP | Calculate overlaps 〈Ψ1(t0)|Ψ2(t)〉 between all pairs of states (between the last and current time step). If followed by “select”, read the list of pairs on the following lines until “end” and calculate overlaps between the specified pairs of states. |
| DMDR | Calculate the Cartesian gradients of the dipole moments and transition dipole moments of all states. |
| ION | Calculate transition properties between neutral and ionic wave functions. |
| THEODORE | Run THEODORE to compute electronic descriptors for all states. |
| MOLDEN | Generate MOLDEN files of the relevant orbitals and copy them to the savedir. |
6.1.2 QM.out Specification
The QM.out file communicates back the results of the quantum chemistry calculation to the dynamics code. After SHARC called QM/runQM.sh, it expects that the file QM/QM.out exists and contains the relevant data.
The following quantities are expected in the file (depending whether the corresponding keyword is in the QM.in file): Hamiltonian matrix, dipole matrices, gradients, nonadiabatic couplings (either NACDR or NACDT), overlaps, wave function phases, property matrices. The format of QM.out is described in the following.
Each quantity is given as a data block, which has a fixed format. The order of the blocks is arbitrary, and between blocks arbitrary lines can be written. However, within a block no extraneous lines are allowed. Each data block starts with a exclamation mark !, followed by whitespace and an integer flag which specifies the type of data:
| 1 | Hamiltonian matrix |
| 2 | Dipole matrices |
| 3 | Gradients |
| 4 | Non-adiabatic couplings (NACDT) |
| 5 | Non-adiabatic couplings (NACDR) |
| 6 | Overlap matrix |
| 7 | Wavefunction phases |
| 8 | Wallclock time for QM calculation |
| 11 | Property matrix (e.g., ionization probabilities) this flag is deprecated |
| 12 | Dipole moment gradients |
| 20 | Property matrices with number and labels (e.g., ionization probabilities) |
| 21 | Property vectors with number and labels (e.g., THEODORE output) |
On the next line, two integers are expected giving the dimensions of the following matrix. Note, that all these matrices must be square matrices. On the following lines, the matrix or vector follows. Matrices are in general complex, and real and imaginary part of each element is given as a pair of floating point numbers.
The following shows an example of a 4×4 Hamiltonian matrix. Note that the imaginary parts directly follow the real parts (in this example, the Hamiltonian is real).
! 1 4 4 -548.6488 0.0000 0.0000 0.0000 0.0003 0.0000 0.0003 0.0000 0.0000 0.0000 -548.6170 0.0000 0.0003 0.0000 0.0003 0.0000 0.0003 0.0000 0.0003 0.0000 -548.5986 0.0000 0.0000 0.0000 0.0003 0.0000 0.0003 0.0000 0.0000 0.0000 -548.5912 0.0000
The three dipole moment matrices (x, y and z polarization) must follow directly after each other, where the dimension specifier must be present for each matrix. The dipole matrices are also expected to be complex-valued.
! 2 2 2 0.1320 0.0000 -0.0020 0.0000 -0.0020 0.0000 -1.1412 0.0000 2 2 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 2 2 2.1828 0.0000 0.0000 0.0000 0.0000 0.0000 0.6422 0.0000
Gradient and nonadiabatic couplings vectors are written as 3×natom matrices, with the x, y and z components of one atom per line. These vectors are expected to be real valued. Each vector is preceeded by its dimensions.
6 3 0.0000 -6.5429 -8.1187 0.0000 5.8586 8.0160 0.0000 6.8428 1.0265 0.0000 6.5429 8.1187 0.0000 -5.8586 -8.0160 0.0000 -6.8428 -1.0265
If gradients are requested, SHARC expects every gradient to be present, even if only some gradients are requested. The gradients are expected in the canonical ordering (see section 8.28), which implies that for higher multiplets the same gradient has to be present several times. For example, with 3 singlets and 3 triplets, SHARC expects 12 gradients in the QM.out file (each triplet has three components with Ms= -1, 0 or 1).
Similarly, for nonadiabatic coupling vectors, SHARC expects all pairs, even between states of different multiplicity. The vectors are also in canonical ordering, where the inner loop goes over the ket states. For example, with 3 singlets and 3 triplets (12 states), SHARC expects 144 (122) nonadiabatic coupling vectors in the QM.out file.
! 5 Non-adiabatic couplings (ddr) (2x2x1x3, real) 1 3 ! m1 1 s1 1 ms1 0 m2 1 s2 1 ms2 0 0.0e+0 0.0e+0 0.0e+0 1 3 ! m1 1 s1 1 ms1 0 m2 1 s2 2 ms2 0 +2.0e+0 0.0e+0 0.0e+0 1 3 ! m1 1 s1 2 ms1 0 m2 1 s2 1 ms2 0 -2.0e+0 0.0e+0 0.0e+0 1 3 ! m1 1 s1 2 ms1 0 m2 1 s2 2 ms2 0 0.0e+0 0.0e+0 0.0e+0
The nonadiabatic coupling matrix (NACDT keyword), the overlap matrix and the property matrix are single n×n matrices (n is the total number of states), respectively, like the Hamiltonian.
The wave function phases are a vector of complex numbers.
The wallclock time is a single real number.
The dipole moment gradients are a list of 3×natom vectors, each specifying the gradient of one polarization of one dipole moment matrix element. In the outmost loop, the bra index is counted, then the ket index, then the polarization. Hence, the respective entry in QM.out would look like (for 2 states and 1 atom):
! 12 Dipole moment derivatives (2x2x3x1x3, real) 1 3 ! m1 1 s1 1 ms1 0 m2 1 s2 1 ms2 0 pol 0 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 1 ms10 m2 1 s2 1 ms2 0 pol 1 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 1 ms10 m2 1 s2 1 ms2 0 pol 2 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 1 ms10 m2 1 s2 2 ms2 0 pol 0 1.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 1 ms10 m2 1 s2 2 ms2 0 pol 1 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 1 ms10 m2 1 s2 2 ms2 0 pol 2 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 2 ms10 m2 1 s2 1 ms2 0 pol 0 1.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 2 ms10 m2 1 s2 1 ms2 0 pol 1 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 2 ms10 m2 1 s2 1 ms2 0 pol 2 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 2 ms10 m2 1 s2 2 ms2 0 pol 0 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 2 ms10 m2 1 s2 2 ms2 0 pol 1 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00 1 3 ! m1 1 s1 2 ms10 m2 1 s2 2 ms2 0 pol 2 0.000000000000E+00 0.000000000000E+00 0.000000000000E+00
The section containing the 2D property matrices consists of three subsequent parts: (i) the number of property matrices contained, (ii) a label for each property matrix (as the property matrices might contain arbitrary data, depending on the interface and the requests), and (iii) the matrices (full, complex-valued matrices like above):
! 20 Property Matrices 2 ! number of property matrices ! Property Matrix Labels (1 strings) Dyson norms Example matrix ! Property Matrices (1x4x4, complex) 4 4 ! Dyson norms 0.000E+00 0.000E+00 0.000E+00 0.000E+00 9.663E-01 0.000E+00 9.663E-01 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 4.822E-01 0.000E+00 4.822E-01 0.000E+00 9.663E-01 0.000E+00 4.822E-01 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 9.663E-01 0.000E+00 4.822E-01 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 4 4 ! Example matrix 1.000E+00 1.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 2.000E+00 2.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 3.000E+00 3.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 4.000E+00 4.000E+00
The section containing the 1D property vectors also consists of three subsequent parts: (i) the number of property vectors contained, (ii) a label for each property vector (as the property vectors might contain arbitrary data, depending on the interface and the requests), and (iii) the vectors (real-valued):
! 21 Property Vectors 2 ! number of property vectors ! Property Vector Labels (2 strings) Om PRNTO ! Property Vectors (9x8, real) ! TheoDORE descriptor 1 (Om) 0.000000000000E+000 4.318700000000E-001 2.688600000000E-001 2.590000000000E-002 ! TheoDORE descriptor 2 (PRNTO) 0.000000000000E+000 2.318700000000E-001 1.688600000000E-001 1.590000000000E-002
6.1.3 Further Specifications
The interfaces may require additional input files beyond QM.in, which contain static information. This may include paths to the quantum chemistry executable, paths to scratch directories, or input templates for the quantum chemistry calculation (e.g. active space specifications, basis sets, etc.).
The dynamics code does not depend on these additional files, but they should all be stored in the QM/ subdirectory.
The current conventions in the SHARC suite are that the quantum chemistry interfaces use two additional input files, one specifying the level of theory (template file, e.g., MOLCAS.template, MOLPRO.template, …) and one specifying the computational resources like paths, memory, number of CPU cores, initial orbital source (resource file, e.g., MOLCAS.resources, MOLPRO.resources, …).
Furthermore, the current interfaces allow to read in initial orbitals (e.g., MOLCAS.*.RasOrb.init, mocoef.init, …).
For interfaces with QM/MM capabilities, additional files could be used to specify connection table, parameters, etc.
6.1.4 Save Directory Specification
The interfaces must be able to save all information necessary for restart to a given directory. The absolute path is written to QM.in by SHARC. Hence, for the trajectories the path to the save directory is always a subdirectory of the working directory of SHARC.
6.2 Overview over Interfaces
The SHARC suite comes with a number of interfaces to different quantum chemistry programs.
Their capabilities and usage are explained in the following sections.
Table 6.3 gives an overview over the capabilities of the interfaces.
Table 6.4 shows the file names for interface-related input files of the different interfaces.
| Method | Program | S2 | SOC | TDMa | Grad. | NACDR | OVLb | DMDR | ION | Theo.c | QM/MM |
| SA-CASSCF | MOLPRO | any | √ | √ | √ | √ | √ | √ | |||
| MOLCAS | any | √ | √ | √ | √ | √d | √ | √ | |||
| COLUMBUS | any | √e | √ | √ | √e | √ | √ | ||||
| BAGEL | any | √ | √ | √ | √ | √ | |||||
| MR-CISD | COLUMBUS | any | √e | √ | √ | √e | √ | √ | |||
| MS-CASPT2 | MOLCAS | any | √ | √ | √d | √ | √d | √ | |||
| XMS-CASPT2 | BAGEL | any | √ | √ | √ | √ | √ | ||||
| TD-DFT | ADF | any | √f | √g | √ | √ | √ | √ | √ | ||
| GAUSSIAN | any | √g | √ | √ | √ | √ | |||||
| ORCA | any | √f | √g | √ | √ | √ | √ | √ | |||
| ADC2 | TURBOMOLE | S, T | √f | √ | √ | √ | √ | √ | |||
| CC2 | TURBOMOLE | S, T | √g | √ | √ | √ | √ | ||||
| XMS-PDFT | MOLCAS | any | √ | √ | √h | ||||||
| CMS-PDFT | MOLCAS | any | √ | √ | √h | ||||||
| Analytical | – | any | √ | √ | √ | √ | √ | ||||
| LVC | – | any | √ | √ | √ | √ | √ |
a TDM: transition dipole moments;
b OVL: wave function overlaps;
c Theo.: THEODORE;
d numerical gradients;
e either NAC or SOC, but not both at the same time;
f SOCs only between singlets and triplets;
g TDMs only between S0 and excited singlets.
h PDFT can only work with curvature driven methods.
| Interface | Template file | Resource file | Initial MOs | QM/MM |
| MOLPRO | MOLPRO.template | MOLPRO.resources | wf.init | |
| wf.<job>.init | ||||
| MOLCAS | MOLCAS.template | MOLCAS.resources | MOLCAS.<mult>.RasOrb.init | MOLCAS.qmmm.table |
| MOLCAS.<mult>.JobIph.init | MOLCAS.qmmm.key | |||
| COLUMBUS | a directory | COLUMBUS.resources | mocoef_mc.init | |
| mocoef_mc.init.<job> | ||||
| molcas.RasOrb.init | ||||
| molcas.RasOrb.init.<job> | ||||
| BAGEL | BAGEL.template | BAGEL.resources | archive.<mult>.init | |
| ADF | ADF.template | ADF.resources | ADF.t21.<job>.init | ADF.qmmm.table |
| ADF.qmmm.ff | ||||
| GAUSSIAN | GAUSSIAN.template | GAUSSIAN.resources | GAUSSIAN.chk.init | |
| GAUSSIAN.chk.<job>.init | ||||
| ORCA | ORCA.template | ORCA.resources | ORCA.gbw.init | ORCA.qmmm.table |
| ORCA.gbw.<job>.init | ORCA.qmmm.ff | |||
| TURBOMOLE | RICC2.template | RICC2.resources | mos.init | RICC2.qmmm.table |
| RICC2.qmmm.ff | ||||
| Analytical | Analytical.template | N/A | N/A | N/A |
| LVC | LVC.template | N/A | N/A | N/A |
6.2.1 Example Directory
The directory $SHARC/../examples/ contains for all quantum chemistry interfaces comprehensively commented examples of input files (template, resource files).
These example files should be regarded as supplementary files to the documentation of the interfaces.
For the interfaces without the possibility for automated template generation (e.g., SHARC_RICC2.py), it is recommended that users copy the example template file and modify it to their needs.
However, note that it might not necessarily work to directly start the respective interface in the example directories.
In order to make the example calculations work, some paths or variables in the resource files need to be adjusted.
If you need automatically working test calculations for SHARC, consider using tests.py instead.
6.3 MOLPRO Interface
The SHARC– MOLPRO interface allows to run SHARC dynamics with MOLPRO‘s CASSCF wave functions. RASSCF is not supported, since on RASSCF level state-averaging over different multiplicities is not possible. The interface uses MOLPRO‘s CI program in order to calculate transition dipole moments and spin-orbit couplings. Gradients and nonadiabatic coupling vectors are calculated using MOLPRO‘s CADPACK code (hence no generally contracted basis sets can be used). In the new version of the interface, overlaps are calculated using the WFOVERLAP code.
Time-derivative couplings (NACDT) are not supported anymore in the SHARC– MOLPRO interface.
Wavefunction phases between the CASSCF and MRCI wave functions are automatically adjusted.
The interface can trivially parallelize the computation of gradients and coupling vectors over several processors.
Execution of parallel MOLPRO binaries is currently not supported.
Important note: It appears that in some cases the sign of the nonadiabatic coupling vectors randomly changes along a trajectory ran with MOLPRO, and that it is not possible to identify this sign change from the MO and CI coefficients.
Hence, propagation with coupling nacdr is currently discouraged for the SHARC– MOLPRO interface.
Alternative possibilities to run SHARC-CASSCF dynamics with nonadiabatic coupling vectors are given by the MOLCAS (section 6.4) and BAGEL (section 6.12) interfaces.
The SHARC– MOLPRO interface needs two additional input files, which should be present in QM/. Those input files are MOLPRO.resources, which contains, e.g., the paths to MOLPRO and the scratch directory, and MOLPRO.template, which is a keyword-argument input file specifying the CASSCF level of theory.
If QM/wf.init is present, it will be used as a MOLPRO wave function file containing the initial MOs.
For calculations with several “jobs” (see below), initial orbitals can also given as QM/wf.<job>.init.
6.3.1 Template file: MOLPRO.template
During the rework of the MOLPRO interface, the template file structure was completely changed.
In the new version, the template file is a keyword-argument list file, similar to the template files of most other interfaces.
A fully commented template file with all possible options is located in $SHARC/../examples/SHARC_MOLPRO/.
For simple cases, an example for the template file looks like this:
basis def2-svp dkho 2 # Douglas-Kroll second order occ 14 closed 10 nelec 24 roots 4 0 3 rootpad 1 0 1
This specifies a SA(4S+3T)-CASSCF(4,4)/def2-SVP calculation for 24 electrons.
Note the rootpad keyword, which adds one singlet and one triplet with zero weight to the state-averaging (so technically this is a SA(5S+4T) calculation, but the results are the same as SA(4S+3T)).
These zero-weight states are sometimes useful to improve convergence of CASSCF.
The new interface can also be used to perform several independent CASSCF calculations for different multiplicities (e.g., one CASSCF for the neutral states and another one for the ionic states).
In this case, each independent CASSCF calculation is called a “job”.
In the template, most settings can be modified independently for each job.
An example is given here:
# In this way, users can employ custom basis sets basis_external /path/to/basisset # no spaces in path allowed dkho 2 # job 1 for singlet+triplet; job 2 for doublets jobs 1 2 1 occ 14 13 # for job 1 and 2 closed 11 10 # for job 1 and 2 nelec 24 23 24 # for job 1 nelec 24 23 24 # for job 2 roots 4 0 3 # for job 1 roots 0 2 0 # for job 2 rootpad 1 0 1 # for job 1 rootpad 0 2 0 # for job 2
This template specifies two jobs, where job 1 should be used to compute singlet and triplet states, and job 2 used for doublet states.
Job 1 is a SA(4S+3T)-CASSCF(2,3) computation, with singlets and triplets each having 24 electrons.
Job 2 is a SA(2D)-CASSCF(3,3) computation, with 23 electrons.
Note how for different jobs it is possible to have different active spaces and state-averaging schemes.
However, keep in mind that all states of a given multiplicity are always calculated in the same job (e.g., it is not possible to have one job for S0 and another job for S1 and S2).
It is also possible to do a mixed input, for example having two jobs, but only giving one number after occ or closed.
The interface provides comprehensive error messages during the template check.
Also note the basis_external keyword. It provides a file, whose content is used in the basis set definition (it is inserted verbatim into basis={...} in the MOLPRO input).
It is possible to use the generated input from the Basis Set Exchange Library, but the basis={ and } need to be deleted from the file.
Remember that molpro_input.py cannot create multi-job templates or templates with the basis_external keyword.
6.3.2 Resource file: MOLPRO.resources
The interface requires some additional information beyond the content of QM.in. This information is given in the file MOLPRO.resources, which must reside in the directory where the interface is started. This file uses a simple “keyword argument” syntax. Comments using # and blank lines are possible, the order of keywords is arbitrary. Lines with unknown keywords are ignored, since the interface just searches the file for certain keywords.
Table 6.5 lists the existing keywords.
A fully commented resource file for this interface with all possible options is located in $SHARC/../examples/SHARC_MOLPRO/.
| Keyword | Description |
| molpro | Is followed by a string giving the path to the MOLPRO directory. This directory should contain the executable molpro.exe. Relative and absolute paths, environment variables and can be used. |
| scratchdir | Is a path to the temporary directory. Relative and absolute paths, environment variables and can be used. If the directory does not exist, the interface will create it. In any case, the interface will delete this directory after the calculation. |
| savedir | Is a path to another temporary directory. Relative and absolute paths, environment variables and can be used. The interface will store files needed for restart there. |
| memory | (int) Memory for MOLPRO and WFOVERLAP in MB. |
| ncpu | (int) Number of CPU cores for parallel computation of gradients/NAC vectors. |
| delay | (float) Time in seconds between starting parallel MOLPRO runs. Useful to lessen the I/O burden when having many runs starting at the same time. |
| gradaccudefault | (float) Default accuracy for CP-MCSCF. |
| gradaccumax | (float) Worst acceptable accuracy for CP-MCSCF (see below). |
| always_orb_init | Do not use the orbital guesses from previous calculations/time steps, but always use the provided initial orbitals. |
| always_guess | Always use the orbital guess from MOLPRO‘s guess module. |
| wfoverlap | Is the path to the WFOVERLAP executable. Relative and absolute paths, environment variables and can be used. |
| numfrozcore | Number of neglected core orbitals for overlap and Dyson calculations. |
| numocc | Number of doubly occupied orbitals for Dyson calculations. |
| nooverlap | Do not save determinant files for overlap computations. |
| debug | Increases the verbosity of the interface. |
| no_print | Reduces interface standard output. |
Mandatory keywords are the paths to MOLPRO, the scratch directory, and to the WFOVERLAP executable (the latter for overlap, Dyson, or NACDR calculations).
Parallel execution of MOLPRO
In the new version of the SHARC– MOLPRO interface, calculations of multiple independent active spaces (“jobs”), of several gradients, and of several nonadiabatic coupling vectors are automatically parallelized over the given number of CPU cores.
Note that in the new version of the interface, MOLPRO calls itself cannot be run with multiple CPUs.
6.3.3 Error checking
The interface is written such that the output of MOLPRO is checked for commonly occuring errors, mostly bad convergence in the MCSCF or CP-MCSCF parts. In these cases, the input is adjusted and MOLPRO restarted. This will be done until all calculations are finished or an unrecoverable error is detected.
The interface will try to solve the following error messages:
EXCESSIVE GRADIENT IN CI This error message can occur in the MCSCF part. The calculation is restarted with a P-space threshold (see MOLPRO manual) of 1. If the error remains, the threshold is quadrupled until the calculation converges or the threshold is above 100.
NO CONVERGENCE IN REFERENCE CI The error occurs in the CI part. The calculation is restarted with a P-space threshold (see MOLPRO manual) of 1. If the error remains, the threshold is quadrupled until the calculation converges or the threshold is above 100.
NO CONVERGENCE OF CP-MCSCF This error occurs when solving the linear equations needed for the calculation of MCSCF gradients or nonadiabatic coupling vectors. In this case, the interface finds in the output the value of closest convergence and restarts the calculation with the value found as the new convergence criterion. This ensures that the CP-MCSCF calculation converges, albeit with lower accuracy for this gradient for this time step.
This error check is controlled by two keywords in the MOLPRO.resources file. The interface first tries to converge the CP-MCSCF calculation to gradaccudefault. If this fails, it tries to converge to the best value possible within 900 iterations. gradaccumax defines the worst accuracy accepted by the interface. If a CP-MCSCF calculation cannot be converged below gradaccumax then the interface exits with an error, leading to the abortion of the trajectory.
6.3.4 Things to keep in mind
Initial orbital guess
For CASSCF calculations it is always a good idea to start from converged MOs from a nearby geometry. For the first time step, if a file QM/wf.init is present, the SHARC– MOLPRO interface will take this file for the starting orbitals. In case of multi-job calculations, separate initial orbitals can be provided with files called QM/wf.<job>.init, where <job> is an integer.
In subsequent calculations, the MOs from the previous step will be used (unless the always_orb_init keyword is used).
Basis sets
Note that the MOLPRO interface cannot calculation SA-CASSCF gradients for generally contracted basis sets (like Dunning’s “cc” basis sets or Roos’ “ANO” basis sets). Only segmented basis sets are allowed, like the Pople basis sets and the “def” family from TURBOMOLE.
In order to employ user-defined basis sets, in the template the keyword basis_external, followed by a filename, can be used.
The interface will then take the content of this file and insert it as basis set definition in the MOLPRO input files (i.e., it will add in the input basis={ <content of the file> }.
Note that the filename must not contain spaces.
6.3.5 Molpro input generator: molpro_input.py
In order to quickly setup simple inputs for MOLPRO, the SHARC suite contains a small script called molpro_input.py. It can be used to setup single point calculations, optimizations and frequency calculations on the HF, DFT, MP2 and CASSCF level of theory. Of course, MOLPRO has far more capabilities, but these are not covered by molpro_input.py. However, molpro_input.py can also prepare template files which are compatible with the SHARC– MOLPRO interface (MOLPRO.template file).
The script interactively asks the user to specify the calculation and afterwards writes an input file and optionally a run script.
Input
Type of calculation
Choose to either perform a single-point calculation or a minimum optimization (including optionally frequency calculation), to generate a template file, or an optimization of a state crossing. For the template generation, no geometry file is needed, but the script looks for a MOLPRO.input in the same directory and allows to copy the settings.
For single-point calculations, optimizations and frequency calculations, files in MOLDEN format called geom.molden, opt.molden or freq.molden, respectively, are created (containing the orbitals, optimization steps and normal modes, respectively). The file freq.molden can be used to generate initial conditions with wigner.py.
Geometry
Specify the geometry file in xyz format. Number of atoms and total nuclear charge is detected automatically. After the user inputs the total charge, the number of electrons is calculated automatically.
In the case of the generation of a template file, instead only the number of electrons is required.
Non-default atomic masses
If a frequency calculation is requested, the user may modify the mass of specific atoms (e.g. to investigate isotopic effects). In the following menu, the user can add or remove atoms with their mass to a list containing all atoms with non-default masses. Each atom is referred to by its number as in the geometry file. Using the command show the user can display the list of atoms with non-default masses. Typing end confirms the list.
Note that when using the produced MOLDEN file later with wigner.py, the user has to enter the same non-default masses again, since the MOLDEN file does not contain the masses and wigner.py has no way to retrieve these numbers.
Level of theory
Supported are Hartree-Fock (HF), density functional theory (DFT), Møller-Plesset perturbation theory (MP2), equation-of-motion coupled-cluster with singles and doubles (EOM-CCSD) and CASSCF (either single-state or state-averaged). All methods (except EOM-CCSD) are compatible with odd-electron wave functions (molpro_input.py will use the corresponding UHF, UMP2 and UKS keywords in the input file, if necessary).
For template generation, state-average CASSCF is automatically chosen. All methods (except EOM-CCSD) can be combined with optimizations and frequency calculations, however, the frequency calculation is much more efficient with HF or SS-CASSCF.
DFT functional
For DFT calculations, enter a functional and choose whether dispersion correction should be applied. Note that the functional is just a string which is not checked by molpro_input.py.
Basis set
The basis set is just a string which is not checked by molpro_input.py.
CASSCF settings
For CASSCF calculations, enter the number of active electrons and orbitals.
For SS-CASSCF, only the multiplicity needs to be specified. For SA-CASSCF, specify the number of states per multiplicity to be included. Note that MOLPRO allows to average over states with different numbers of electrons. This feature is not supported in molpro_input.py. However, the user can generate a closely-matching input and simply add the missing states to the CASSCF block manually.
For optimizations at SA-CASSCF level, the state to be optimized has to be given. For crossing point optimizations, two states need to be entered. The script automatically detects whether a conical intersection or a crossing between states of different multiplicity is requested and sets up the input accordingly.
EOM-CCSD settings
EOM-CCSD calculations allow to calculate relatively accurate excited-state energies and oscillator strengths from a Hartree-Fock reference, but only for singlet excited states.
The user has to specify the number of states to be calculated. If only one state is requested, the script will setup a regular ground state CCSD calculation, while for more than one states, an EOM-CCSD calculation is setup.
Note that the calculation of transition properties takes twice as long as the energy calculation itself.
Memory
Enter the amount of memory for MOLPRO. Note that values smaller than 50 MB are ignored, and 50 MB are used in this case.
Run script
If requested, the script also generates a simple Bash script (run_molpro.sh) to directly execute MOLPRO. The user has to enter the path to MOLPRO and the path to a suitable (fast) scratch directory.
Note that the scratch directory will be deleted after the calculation, only the wave function file wf will be copied back to the main directory.
6.4 MOLCAS Interface
The SHARC– MOLCAS interface can be used to conduct excited-state dynamics based on MOLCAS‘ CASSCF, SS-CASPT2, MS-CASPT2, MC-PDFT, XMS-PDFT, or CMS-PDFT methods.
RASSCF wave functions are not supported currently.
For SS-CASPT2, MS-CASPT2, and XMS-PDFT, only numerical gradients are available.
The support for MC-PDFT, XMS-PDFT, or CMS-PDFT is currently to be regarded as experimental.
Currently, SHARC is tested to work with OPENMOLCAS 18-23.
Versions of MOLCAS newer than 8.3 should also work, but no guarantee is given.
Note that within this Manual, MOLCAS and OPENMOLCAS are used synonymously, because from SHARC‘s viewpoint, they only differ in the driver program (pymolcas or molcas.exe).
Important note: please make sure that a copy of the respective driver program (pymolcas or molcas.exe) is located in the $MOLCAS/bin/ directory, as the interface will search this directory for these programs to distinguish between MOLCAS and OPENMOLCAS.
Alternatively, give the path to the driver with the driver keyword in MOLCAS.resources.
The interface uses the modules GATEWAY, SEWARD (integrals), RASSCF (wave function, energies), RASSI (transition dipole moments, spin-orbit couplings, overlaps), MCLR, and ALASKA (gradients).
The CASPT2 and MCPDFT modules are used for their respective energy methods.
For CASPT2, MS-CASPT2, and XMS-PDFT, numerical gradients can be calculated, where the interface itself controls the calculations at the displaced geometries.
The interface can also numerically differentiate dipole moments and spin-orbit couplings.
For CASSCF, MC-PDFT, and CMS-PDFT, analytical nonadiabatic coupling vectors are available.
Using the WFOVERLAP code, it is possible to calculate Dyson norms between neutral and ionic states.
Note that (unlike MOLPRO) MOLCAS cannot average over states of different multiplicities; hence, the multiplicities are always computed in separate jobs which all share the same CAS settings.
The SHARC– MOLCAS interface furthermore allows to perform QM/MM dynamics (CASSCF plus force fields), through the MOLCAS– TINKER interface.
The interface needs two additional input files, a template file for the quantum chemistry (file name is MOLCAS.template) and a resource file (MOLCAS.resources). If the interface finds files with the name QM/MOLCAS.<i>.JobIph.init or QM/MOLCAS.<i>.RasOrb.init, they are used as initial wave function files, where <i> is the multiplicity. In the case of QM/MM calculations, two more input files are needed: MOLCAS.qmmm.key, which contains the path to the force field parameters and the partitioning into QM and MM regions, and MOLCAS.qmmm.table, which contains the connectivity and force field IDs per atom.
6.4.1 Template file: MOLCAS.template
This file contains the specifications for the wave function. Note that this is not a valid MOLCAS input file. No sections like $GATEWAY, etc., can be used. The file only contains a number of keywords, given in table 6.6.
The actual input files are automatically generated.
A fully commented template file with all possible options is located in $SHARC/../examples/SHARC_MOLCAS/.
| Keyword | Description |
| basis | The basis set used. Note that some basis sets (e.g., Pople basis sets) do not work, since the spin-orbit integrals cannot be calculated. |
| baslib | Can be used to provide the path to a custom basis set library (analogous to the baslib keyword in MOLCAS). |
| nactel | Number of active electrons for CASSCF. |
| ras2 | Number of active orbitals for CASSCF. |
| inactive | Number of inactive orbitals. |
| roots | Followed by a list of integers, giving the number of states per multiplicity in the state-averaging procedure. |
| rootpad | Followed by a list of integers, giving the number of extra, zero-weight states in the state-averaging. |
| method | Followed by a string, which is one of “CASSCF”, “CASPT2”, “MS-CASPT2”, “XMS-PDFT”, or “CMS-PDFT” (case insensitive), defining the level of theory. Default is “CASSCF”. |
| functional | Followed by a string, which is one of “t:PBE”, “ft:PBE”, “t:BLYP”, “ft:BLYP”, “t:revPBE”, “ft:revPBE”, “t:LSDA”, or “ft:LSDA” (case insensitive), defining the functionals used in multiconfigurational pair density functional theory. |
| douglas-kroll | Activates the use of the scalar-relativistic DK Hamiltonian. Usually not needed, as Molcas picks the Hamiltonian based on the choice of basis function. |
| ipea | Followed by a float giving the IP-EA shift for CASPT2 (see MOLCAS manual for more information). The default is 0.25, as in MOLCAS. |
| imaginary | Followed by a float giving the imaginary level shift for CASPT2 (see MOLCAS manual for more information). The default is 0.0, as in MOLCAS. |
| frozen | Number of frozen orbitals for CASPT2. Default is -1, which lets MOLCAS choose the number of frozen orbitals. |
| cholesky | Activates Cholesky decomposition in MOLCAS. Recommended for large basis sets. Will use analytical gradients for CASSCF. Default is to use regular 4-electron integrals. |
| gradaccudefault | (float) Default accuracy for CP-MCSCF. |
| gradaccumax | (float) Worst acceptable accuracy for CP-MCSCF. |
| displ | Cartesian displacement (in Å) for numerical differentiation (default 0.005 Å). |
| qmmm | Activates the QM/MM mode. In this case, two more input files need to be present (see below). |
| pcmset | Activates the PCM mode. Three arguments follow: the solvent (a string, default “water”), the AARE value (a float, default 0.4, optional), the RMIN value (a float, default 1.0, optional). Check MOLCAS manual for details. |
| pcmstate | Defines the state for which the PCM charges will be optimized. Followed by two numbers: multiplicity (1=singlet, …) and state (1=lowest state of that multiplicity). Default is the first state according to the state request. |
Simple template files can be setup with the tool molcas_input.py.
6.4.2 Resource file: MOLCAS.resources
The file MOLCAS.resources contains mainly paths (to the MOLCAS executables, to the scratch directory, etc.). This file must reside in the same directory where the interface is started. It uses a simple “keyword argument” syntax. Comments using # and blank lines are possible, the order of keywords is arbitrary. Lines with unknown keywords are ignored, since the interface just searches the file for certain keywords.
Table 6.7 lists the existing keywords.
A fully commented resource file for this interface with all possible options is located in $SHARC/../examples/SHARC_MOLCAS/.
| Keyword | Description |
| molcas | Is the path to the OPENMOLCAS installation. This directory should contain subdirectories like bin/, basis_library/, data/, or lib/. Relative and absolute paths, environment variables and can be used. The interface will set $MOLCAS to this path. If this keyword is not present in MOLCAS.resources, the interface will use the environment variable $MOLCAS, if it is set. |
| tinker | The path to the TINKER installation directory, usable with MOLCAS. This directory should contain the bin/ subdirectory. |
| wfoverlap | Is the path to the WFOVERLAP executable. Relative and absolute paths, environment variables and can be used. Only needed for Dyson norm calculations. |
| scratchdir | Is a path to the temporary directory. Relative and absolute paths, environment variables and can be used. If it does not exist, the interface will create it. In any case, the interface will delete this directory after the calculation. |
| savedir | Is a path to another temporary directory. Relative and absolute paths, environment variables and can be used. The interface will store files needed for restart there. |
| memory | The memory usable by MOLCAS. The interface will set $MOLCASMEM to this value. The default is 10 MB. |
| ncpu | The number of CPUs used by the interface. If zero or negative, one CPU will be used and all subtasks (Hamiltonian, dipole moments, analytical gradients, overlaps) will be done in one MOLCAS call. If positive, analytical gradients will be calculated by separate calls to MOLCAS, parallelized over the given number of CPUs. |
| mpi_parallel | Uses MPI parallel MOLCAS runs. The number of cores is dynamically chosen based on the available cores and the number of tasks (energies, gradients, displacements). |
| schedule_scaling | Gives the expected parallelizable fraction of the MOLCAS run time (Amdahl’s law). With a value close to zero, the interface will try to run all jobs at the same time. With values close to one, jobs will be run sequentially with the maximum number of cores. |
| delay | Followed by a float giving the delay in seconds between starting parallel jobs to avoid excessive disk I/O. |
| always_orb_init | Do not use the orbital guesses from previous calculations/time steps, but always use the provided initial orbitals. |
| always_guess | Always use the orbital guess from MOLCAS‘s guessorb module. |
| debug | Increases the verbosity of the interface. |
| no_print | Reduces interface standard output. |
Note that the interface sets all environment variables necessary to run MOLCAS (e.g., $MOLCAS, $MOLCASMEM, $WorkDir ,$Project) automatically, based on the input from MOLCAS.resources and QM.in.
Some explanations on parallelization: There are two parallel modes in which the interface can act. In the first mode, the wave function and expectation values are calculated serially first, and then all analytical gradients are computed in parallel, over the given number of CPUs. If the number of CPUs is one, then still the interface prepares independent computations for each gradient, and runs those sequentially on one CPU. If the given number of CPUs is negative or zero, then the gradients are not prepared as separate MOLCAS calculations, but together with the other quantities. The latter variant has less overhead, but is only recommended if the user is sure that the gradient calculations (MCLR) will converge in virtually all cases. If MCLR does not converge occasionally, it is advisable to use NCPU=1 instead of NCPU ≤ 0. The interface will then try to rerun MCLR until it converges.
In the second parallelization mode, used for numerical gradients, the central point is calculated first and then all displacements are computed in parallel. This mode will be used for gradients on CASPT2, MS-CASPT2 and XMS-PDFT level, for spin-orbit/dipole moment derivatives on all levels, and with PCM on all levels. In this mode there is no distinction between NCPU=1 and NCPU ≤ 0. Note that numerical gradients are always automatically computed for all states or state-pairs. Hence, in numerical-gradient mode there is no advantage of using the grad_select keyword in sharc.x. Also note that the SHARC– MOLCAS interface currently does not handle multiple jobs in the same time step correctly. Accordingly, for CASPT2 dynamics, one needs to employ the select_directly and grad_all keywords.
6.4.3 Template file generator: molcas_input.py
This is a small interactive script to generate template files for the SHARC– MOLCAS interface. It simply queries the user for some input parameters and then writes the file MOLCAS.template, which can be used to run SHARC simulations with the SHARC– MOLCAS interface.
The input generator can also be used to write proper MOLCAS input files for single-point calculations and optimizations/frequency calculations on CASSCF and (MS-)CASPT2 level of theory.
Type of calculation
Choose to either perform a single-point calculation or a minimum optimization (including optionally frequency calculation), or to generate a template file. For the template generation, no geometry file is needed, but the script looks for a MOLCAS.input in the same directory and allows to copy the settings.
For single-point calculations, optimizations and frequency calculations, files in MOLDEN format are created (containing the orbitals, optimization steps and normal modes, respectively). The file MOLCAS.freq.molden can be used to generate initial conditions with wigner.py.
Geometry file
The geometry file is only used to calculate the nuclear charge.
Charge
This is the overall charge of the molecule. This number is used with the nuclear charge to calculate the number of electrons.
Method
Choose either CASSCF or CASPT2. Multi-state CASPT2 can be requested later.
Basis set
This is simply a string, which is not checked by the script to be a valid basis set of the MOLCAS library.
Number of active electrons and orbitals
These settings are necessary for the definition of the CASSCF wave function. The number of inactive orbitals is automatically calculated from the total number of electrons and the number of active electrons.
States for state-averaging
For each multiplicity, the number of states for the state-averaging procedure must be equal or larger than the number of states used in the dynamics.
Further settings
Depending on the run type and method, the script might ask further questions regarding the root to optimize, CASPT2 settings (whether to do multi-state CASPT2, IPEA shift, imaginary level shift), or whether a spin-orbit RASSI should be performed (for input file generation only).
6.4.4 QM/MM key file: MOLCAS.qmmm.key
This file defines some aspects of the QM/MM calculation. An example is given below:
parameters $MOLCAS/tinker/params/amber99sb.prm QMMM 18 QM -1 15 MM -16 18 QMMM-ELECTROSTATICS ESPF
The first line defines the force field parameters, which are read from TINKER‘s library here. Note that in the file path, environment variables are expanded by the interface.
The next three lines define the QM and MM regions of the system, where in this case atoms 1-15 are in the QM region and atoms 16-18 are in the MM region (note the minus signs indicating the begin of an interval). The last line defines how to treat electrostatics in the calculation (currently, only ESPF is implemented for MOLCAS, so this line has to be present as shown, or omitted).
6.4.5 QM/MM connection table file: MOLCAS.qmmm.table
This is the template to generate the TINKER xyz file, which besides the geometry contains the force field atom type number and the connectivity information. A sample looks like:
8 1 N* 1.6 3.3 -2.0 1132 2 2 CK 0.3 3.1 -2.6 1136 1 3 4 3 H5 -0.4 2.9 -1.9 1145 2 4 NB 0.3 3.2 -3.9 1135 2 5 5 CB 1.6 3.5 -4.2 1134 4 6 6 CA 2.2 3.8 -5.4 1140 5 7 7 N2 1.6 3.8 -6.6 1142 6 8 8 H 2.1 3.9 -7.5 1143 7
The first line contains the number of atoms. In each following line, the atom index, the atomic symbol (or name), the coordinates of the atom, the force field atom type number and the index of atoms bonded to the current atom. The coordinates in this file are not used and are replaced by the SHARC– MOLCAS interface by the actual coordinates of the atoms. The atom type number can be looked up in the .prm files of the TINKER parameter directory.
6.5 COLUMBUS Interface
The SHARC– COLUMBUS interface allows to run SHARC dynamics based on COLUMBUS‘ CASSCF, RASSCF and MRCI wave functions.
The interface is compatible to COLUMBUS calculations utilizing the COLUMBUS– MOLCAS interface ( SEWARD integrals and ALASKA gradients), or using the DALTON integral code distributed with COLUMBUS.
Using SEWARD integrals, spin-orbit couplings can be calculated, but no nonadiabatic couplings (only overlaps can thus be used).
Using DALTON integrals, spin-orbit couplings are not possible, but nonadiabatic couplings can be calculated.
The CASSCF step can be done with either COLUMBUS‘ mcscf code (all features available) or with MOLCAS‘ rasscf code (faster, but no gradients possible).
The interface utilizes the WFOVERLAP program to calculate the overlap matrices.
The interface can also calculate Dyson norms between neutral and ionic wave functions using the WFOVERLAP code.
The interface needs as additional input the file QM/COLUMBUS.resources and a template directory containing all input files needed for the COLUMBUS calculations. Initial MOs can be given in the file QM/mocoef_mc.init.
For multiple jobs, initial MOs can be given as QM/mocoef_mc.init.<job>.
For runs with rasscf, initial MOs have to be given as molcas.RasOrb.init or molcas.RasOrb.init.<job>.
6.5.1 Template input
The interface does not generate the full COLUMBUS input on-the-fly. Instead, the interface uses an existing set of input files and performs only necessary modifications (e.g., the number of states). The set of input files must be provided by the user. Please see the COLUMBUS online documentation and, most importantly, the
COLUMBUS SOCI tutorial for a documentation of the necessary input.
The SHARC tutorial also has a section about generating the required COLUMBUS input file collection.
An example template directory is located in $SHARC/../examples/SHARC_COLUMBUS/.
Generally, the input consists of a directory with one subdirectory with input for each multiplicity (singlets, doublets, triplets, …). However, even-electron wave functions of different multiplicities can be computed together in the same job if spin-orbit couplings are desired. Independent multiple-DRT inputs (ISC keyword) are also acceptable. Note that symmetry is not allowed when using the interface.
The path to the template directory must be given in COLUMBUS.resources, along with the other resources settings.
Integral input
The interface is able to use input for calculations using SEWARD or DALTON integrals.
If you want to calculate SOCs, you have to use SEWARD and have to include the AMFI keyword in the integral input.
If you use DALTON, SOCs are not available, but it is possible to compute nonadiabatic couplings.
It is important to make sure that the order of atoms in the template input files and in the SHARC input is consistent.
Furthermore, it is necessary to prepare all template subdirectories with the same integral code and the same AO basis set.
MCSCF input
The MCSCF section can use any desired state-averaging scheme, since the number of states in MCSCF is independent of the number of states in the MRCI module. However, frozen core orbitals in the MCSCF step are not possible (since otherwise gradients cannot be computed). Prepare the MCSCF input for CI gradients. It is advisable to use very tight MCSCF convergence criteria.
If gradients are not needed, you can also manually prepare a MOLCAS RASSCF input in molcas.input, in order to use MOLCAS RASSCF instead of COLUMBUS MCSCF (see molcas_rasscf keyword).
MRCI input
Either prepare a single-DRT input without SOCI (to cover a single multiplicity), a single-DRT input with SOCI and a sufficient maximum multiplicity for spin-orbit couplings or an independent multiple-DRT input (as, e.g., for ISC optimizations). Make sure that all multiplicities are covered with all input directories.
In the MRCI input, make sure to use sequential ciudg. Also take care to setup gradient input on MRCI level.
Job control
Setup a single-point calculation with the following steps:
- SCF
- MCSCF
- MR-CISD (serial operation) or SO-CI coupled to non-rel CI (for SOCI DRT inputs)
- one-electron properties for all methods
- transition moments for MR-CISD
- nonadiabatic couplings (and/or gradients)
Request first transition moments and interstate couplings (or alternatively full nonadiabatic couplings if Dalton integrals are used) in the following dialogues. Analysis in internal coordinates and intersection slope analysis are not required.
6.5.2 Resource file: COLUMBUS.resources
Beyond the information from QM.in the interface needs additional input, which is read from the file COLUMBUS.resources. Table 6.8 lists the keywords which can be given in the file.
A fully commented resource file with all possible options is located in $SHARC/../examples/SHARC_COLUMBUS/.
|
Table 6.8: Keywords for the COLUMBUS.resources file.
|
||
| Keyword | Description | |
|
columbus |
Path to the COLUMBUS main directory.This directory should contain executables like runc, mcscf.x, cidrt.x, or ciudg.x. Relative and absolute paths, environment variables and can be used. | |
| molcas | Path to the MOLCAS main directory. Relative and absolute paths, environment variables and can be used. This path is only used for overlap/Dyson calculations (since in this case the interface calls MOLCAS explicitly). Otherwise COLUMBUS will use the path to MOLCAS specified during the installation of COLUMBUS. | |
| wfoverlap | Path to the wave function overlap and Dyson norm code. Relative and absolute paths, environment variables and can be used. Only necessary if overlaps or Dyson norms are calculated. Needs a suitable code that computes overlaps of CI wave functions. | |
| runc | Path to the runc script for COLUMBUS execution. Default is $COLUMBUS/runc. This keyword is intended for users who like to modify runc. | |
| scratchdir | Path to the temporary directory, used to perform the COLUMBUS calculations. Relative and absolute paths, environment variables and can be used. If it does not exist, the interface will create it. The interface will delete this directory after the calculation. | |
| savedir | Path to another directory. Relative and absolute paths, environment variables and can be used. The interface will store files needed for restart in this directory. Default is a subdirectory of the directory where the interface is executed. | |
| memory | (integer, MB) Memory for COLUMBUS. The maximum amount of memory used by the wfoverlap code is also controlled with this keyword. | |
| ncpu | (integer) Number of CPU cores to use for SMP-parallel execution of the wfoverlap code. Parallel COLUMBUS is currently not supported. | |
| wfthres | (float) Gives the amount of wave function norm which will be kept in the truncation of the determinant files for Dyson and overlap calculations. Default is 0.97 (i.e., the wave functions in the determinant files will have a norm of 0.97) | |
| nooverlap | (no argument) Do not keep the files necessary to calculate wave function overlaps in the next time step. If Dyson norms are requested, nooverlap is ignored. | |
| always_orb_init | Use the initial MO guess (mocoef_mc.init) for all time steps, not only for the first step. | |
| always_guess | In all time steps obtain the MO guess from an SCF calculation, instead of using the MOs from the previous step. | |
| integrals | Followed by a string which is either seward or dalton. Chooses the integral program for COLUMBUS. Note that with DALTON integrals SOC is not available. Default is seward. | |
| molcas_rasscf | Use MOLCAS‘ RASSCF program instead of COLUMBUS‘ MCSCF program. Needs a properly prepared COLUMBUS input (&RASSCF section in molcas.input). Note that gradients are not available in this mode. | |
| template | Is followed by the path to the directory containing the template subdirectories. Relative and absolute paths, environment variables and can be used. See also 6.5.3. | |
| DIR | See 6.5.3. | |
| MOCOEF | See 6.5.3. | |
| numfrozcore | Can be used to override the number of frozen orbitals in Dyson calculations (Default is the value from the cidrt input). | |
| numocc | Can be used to declare orbitals above the frozen orbitals as doubly occupied in Dyson calculations. No ionization from these orbitals is calculated, but otherwise they are considered in the Dyson calculations. Default is zero. | |
| debug | Increases the verbosity of the interface. | |
| no_print | Reduces interface standard output. | |
6.5.3 Template setup
The template directory contains several subdirectories with input for different multiplicities. An example is given in figure 6.2. In COLUMBUS.resources, the user has to associate each multiplicity to a subdirectory. The line “DIR 1 Sing_Trip” would make the interface use the input files from the subdirectory Sing_Trip when calculating singlet states (the 1 refers to singlet calculations). All calculations using a particular input subdirectory are called a job.
Additionally, the user must specify which job(s) provide the MO coefficients (e.g., the calculation for doublet states could be based on the same MOs as the singlet and triplet calculation). The line “MOCOEF Doub_Quar Sing_Trip” would tell the interface to do a MCSCF calculation in the Sing_Trip job, and reuse the MOs when doing the Doub_Quar job without reoptimizing the MOs.
6.6 Analytical PESs Interface
The SHARC suite also contains an interface which allows to run dynamics simulations on PESs expressed with analytical functions.
In order to allow dynamics simulations in the same way as it is done on-the-fly, the interface uses two kinds of potential couplings:
- couplings that are pre-diagonalized in the interface (yielding the equivalent of the MCH basis),
- couplings given by the interface to SHARC as off-diagonal elements.
The interface needs one additional input file, called Analytical.template, which contains the definitions of all analytical expressions.
6.6.1 Parametrization
The interface has to be provided with analytical expressions for all matrix elements of the following matrices in the diabatic basis:
- Hamiltonian: H
- Derivative of the Hamiltonian with respect to each atomic coordinate: Hxi
- (Transition) dipole matrices for each polarization direction: Mi
- Real and imaginary part of the SOC matrix: Σ
- (Optionally) the derivatives of the transition dipole matrices: Di,xj
The diabatic Hamiltonian is diagonalized:
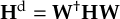 |
(6.1) |
Then the following calculations lead to the MCH matrices which are passed to SHARC:
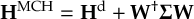 |
(6.2) |
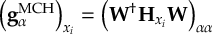 |
(6.3) |
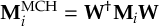 |
(6.4) |
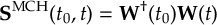 |
(6.5) |
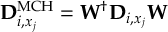 |
(6.6) |
The MCH Hamiltonian is the diagonalized diabatic Hamiltonian plus the SO matrix transformed into the MCH basis. The gradients in the MCH basis are obtained by transforming the derivative matrices into the MCH basis. The dipole matrices are also simply transformed into the MCH basis. The overlap matrix is the overlap of old and new transformation matrix.
6.6.2 Template file: Analytical.template
The interface-specific input file is called Analytical.template. It contains the analytical expressions for all matrix elements mentioned above. All analytical expressions in this file are evaluated considering the atomic coordinates read from QM.in.
The file consists of a file header and the file body. The file body consists of variable definition blocks and matrix blocks.
A commented template file is located in $SHARC/../examples/SHARC_Analytical/.
Header
The header looks similar to an xyz file:
2 2 I xI 0 0 Br xBr 0 0
Here, the first line gives the number of atoms and the second line the number of states.
On the remaining lines, each Cartesian component of the atomic coordinates is associated to a variable name, which can be used in the analytical expressions. If a zero (0) is given instead of a variable name, then the corresponding Cartesian coordinate is neglected. In the above example, the variable name xI is associated with the x coordinate of the first atom given in QM.in. The y and z coordinates of the first atom are neglected.
All variable names must be valid Python identifiers and must not start with an underscore. Hence, all strings starting with a letter, followed by an arbitrary number of letters, digits and underscores, are valid. It is not allowed to use a variable name twice.
Note that the file header also contains the atom labels, which are just used for cross-checking against the atom labels in QM.in.
The file header must not contain comments, neither at the end of a line nor separate lines. Also, blank lines are not allowed in the header. After the last line of the header (where the variables for the natom-th atom are defined), blank lines and comments can be used freely (except in matrix blocks).
Variable definition blocks
Variable definition blocks can be used to store additional numerical values (beyond the atomic coordinates) in variables, which can then be used in the equations in the matrix blocks. The most obvious use for this is of course to define values which will appear several times in the equations.
A variable definition block looks like:
Variables A1 0.067 g1 0.996 # Trailing comment # Blank line with comment only R1 4.666 End
Each block starts with the keyword “Variables” and is terminated with “End”. Inbetween, on each line a variable name and the corresponding numerical value (separated by blanks) can be given. Note that the naming conventions given above also apply to variables defined in these blocks.
There can be any number of complete variable definitions blocks in the input file. All blocks are read first, before any matrix expressions are evaluated. Hence, the relative order of the variable blocks and the matrix blocks does not matter. Also, note that variable names must not appear twice, so variables cannot be redefined halfway through the file.
Matrix blocks
The most important information in the input file are of course contained in the expressions in the matrix blocks. In general, a matrix block has the following format:
Matrix_Identifier V11 V12, V22 V13, V23, V33 ...
The first line identifies the type of matrix. Those are valid identifiers:
| Hamiltonian | Defines the Hamiltonian including the diabatic potential couplings. |
| Derivatives followed by a variable name | Derivative of the Hamiltonian with respect to the given variable. |
| Dipole followed by 1, 2 or 3 | (Transition) dipole moment matrix for Cartesian direction x, y or z, respectively. |
| Dipolederivatives followed by 1, 2 or 3 followed by a variable name | Derivative of the respective dipole moment matrix. |
| SpinOrbit followed by R or I | Real or Imaginary (respectively) part of the spin-orbit coupling matrix Σ. |
Since the interface searches the file for these identifiers starting from the top until it is found, for each matrix only the first block takes effect. Note that the Hamiltonian and all relevant derivatives must be present. If dipole matrix, dipole derivative matrix or SO matrix definitions are missing, they will be assumed zero.
In the lines after the identifier, the expressions for each matrix element are given. Note the lower triangular format (all matrices are assumed symmetric, except the imaginary part of the SO matrix, which is assumed antisymmetric). Matrix elements must be separated by commas (so that whitespace can be used inside the expressions). There must be at least as many lines as the number of states (additional lines are neglected). If any line or matrix element is missing, the interface will abort.
An examplary block looks like:
Hamiltonian A1*( (1.-math.exp(g1*(R1-xI+xBr)))**2-1.), 0.0006, 3e-5*(xI-xBr)**2
It is important to understand that the expressions are directly evaluated by the Python interpreter, hence all expressions must be valid Python expressions which evaluate to numeric (integer or float) values. Only the variables defined above can be used.
Note that exponentiation in Python is **. In order to provide most usual mathematical functions, the math module is available. Among others, the math module provides the following functions:
- math.exp(x): Exponential function
- math.log(x): Natural logarithm
- math.pow(x,y): xy
- math.sqrt(x): √x
- math.cos(x), math.sin(x), math.tan(x)
- math.acos(x), math.asin(x), math.atan(x)
- math.atan2(y,x): tan−1([y/x]), as in many programming languages (takes care of phases)
- math.pi, math.e: π and Euler’s number
- math.cosh(x), math.sinh(x): Hyperbolic functions (also tanh, acosh, asinh, atanh are available)
6.7 ADF Interface
The SHARC-ADF interface allows to run SHARC simulations with ADF’s TD-DFT functionality.
The interface is compatible with restricted and unrestricted ground states, but not with symmetry.
Spin-orbit couplings are obtained with the perturbative ZORA formalism, and wave function overlaps from the WFOVERLAP code are available (but no nonadiabatic couplings).
Dyson norms can also be computed through the WFOVERLAP code.
THEODORE (version 2.0 and higher) can be used to perform automatic wave function analysis.
QM/MM is possible through ADF’s internal implementation, but only mechanical embedding is currently available in ADF.
The interface needs two additional input files, a template file for the quantum chemistry (file name is ADF.template) and a resource file (ADF.resources).
If files QM/ADF.t21.<job>.init are are present, they are used to provide an initial orbital guess for the SCF calculation of the respective job.
Before running the ADF interface, it is necessary to source one of the adfrc files, so that Python can find the KFFile module of ADF.
Note that since SHARC2.1, only ADF2019 and newer are supported by SHARC_ADF.py, because older ADF versions do not ship with the KFFile module.
Also note that KFFile requires Python 3 (version 3.5 or higher), hence SHARC_ADF.py is a Python 3 script, unlike every other script in the SHARC package.
6.7.1 Template file: ADF.template
This file contains the specifications for the quantum chemistry calculation. Note that this is not a valid ADF input file. The file only contains a number of keywords, given in table 6.9. The actual input for ADF will be generated automatically through the interface.
In order to enable many functionalities of ADF and to allow fine-tuning of the performance for large calculations, the template has a relatively large number of keywords.
A fully commented template file-with all possible options, a comprehensive descriptions, and some practical hints-is located in $SHARC/../examples/SHARC_ADF/ADF.template.
We recommend that users start from this template file and modify it appropriately for their calculations.
| Keyword | Description |
| relativistic | If not given, perform a nonrelativistic calculation. Otherwise, copy the line verbatim to the ADF input. |
| basis | Gives the basis set for all atoms (default SZ). |
| basis_path | gives the path to the basis library of ADF ( and $ can be used). |
| basis_per_element | Followed by an elemental symbol (e.g., “Fe”, “H.1”) and then by a path to the desired ADF basis set file. Files with frozen core should not be used. |
| define_fragment | Followed by an elemental symbol (e.g., “Fe”, “H.1”) and then by a list of atom numbers which should belong to this atom type. |
| functional | Followed by two strings. First argument gives the type of functional (LDA, GGA, hybrid), second argument gives the functional (VWN, BP86, B3LYP, …). |
| functional_xcfun | Enables functional evaluation with the XCFun library within ADF. |
| dispersion | If present, is written verbatim to ADF input with all arguments. |
| charge | Sets the total charge of the (QM) system. Can be either followed by a single integer (then the interface will automatically assign the charges to the multiplicities) or by one charge per multiplicity. Automatic assignment might not work correctly for QM/MM computations. |
| totalenergy | Activates the computation of total energies (by default, ADF computes binding energies). Does not work for relativistic or QM/MM calculations. |
| cosmo | Followed by a string giving a solvent. Activates COSMO (no gradients possible). |
| cosmo_neql | Activates non-equilibrium solvation, which is needed for vertical excitation calculations. Is followed by a float giving the square of the refractive index of the solvent. |
| grid | Followed by two strings (e.g., beckegrid normal or integration 4.0) defining which integration grid and accuracy to use. For details, see the example template file. |
| grid_qpnear | Followed by a float giving the maximum distance (in Bohr) an MM point charge can have from a QM atom, such that integration grid points are generated around the MM charge. |
| grid_per_atom | Followed by a string (e.g., basic, normal, good) and a list of the atoms which should have the given integration accuracy. Can be used multiple times with different qualities. |
| fit | Followed by two strings (e.g., zlmfit normal or stofit) defining which Coulomb integration method and accuracy to use. For details, see the example template file. |
| fit_per_atom | Works like grid_per_atom, but for the Coulomb method accuracy. |
| exactdensity | Enables the exactdensity keyword in the ADF input. |
| rihartreefock | Followed by a quality keyword (e.g., basic, normal, good). If not present, the old HF exchange routines in ADF are used. |
| rihf_per_atom | Works like grid_per_atom, but for the RI Hartree Fock method. |
| occupations | If present, the foll line is copied verbatim to the ADF input. |
| scf_iterations | Followed by the maximum number of SCF iterations (default: 100) |
| linearscaling | Followed by an integer (between 0 and 99), which controls whether certain terms are neglected in ADF. |
| cpks_eps | Followed by a float (default 0.0001) giving the convergence threshold in the CPKS equations for excited-state gradients. |
| no_tda | This keyword deactivates TDA, which the interface requests by default. |
| fullkernel | Uses the full (non-ALDA) kernel in TDDFT. Not compatible with gradients, and automatically activates functional_xcfun. |
| paddingstates | Followed by a list of integers, which give the number of extra states to compute by ADF, but which are neglected in the output. Should not be changed between time steps, as this will break ADF’s restart routines. |
| dvd_vectors | Number of Davidson vectors. Default: min(40,nstates+40). |
| dvd_tolerance | Energy convergence criterion for the excited states (in Hartree). |
| dvd_residu | Residual norm convergence criterion for the excited states. |
| dvd_mblocksmall | Activates the mblocksmall keyword in the ADF input. This undocumented keyword changes how the Davidson algorithm works. In reduces computation time, but might lead to incomplete convergence in certain cases. |
| unrestricted_triplets | Requests that the triplets are calculated in a separate job from an unrestricted ground state. Default is to compute triplets as linear response of the restricted singlet ground state. |
| modifyexcitations | Followed by an integer, indicating that excitation should only be possible from the first n MOs. Can be used to compute core-excitation states (for X-Ray spectra). |
| qmmm | Activates QM/MM. In this case, the interface will look for two additional input files (see below). |
| qmmm_coupling | Followed by an integer (1=mechanical embedding, 2=electrostatic embedding). Default is 2. |
6.7.2 Resource file: ADF.resources
The file ADF.resources contains mainly paths (to the ADF executables, to the scratch directory, etc.) and other resources, plus settings for wfoverlap.x and THEODORE. This file must reside in the same directory where the interface is started. It uses a simple “keyword argument” syntax. Comments using # and blank lines are possible, the order of keywords is arbitrary. Lines with unknown keywords are ignored, since the interface just searches the file for certain keywords.
Table 6.10 lists the existing keywords.
A fully commented resource file with all possible options and comprehensive descriptions is located in $SHARC/../examples/SHARC_ADF/.
| Keyword | Description |
| adfhome | Is the path to the ADF installation. Relative and absolute paths, environment variables and can be used. The interface will set $ADFHOME to this path, and will also set $ADFBIN to $ADFHOME/bin/. |
| scmlicense | Is the path to the ADF license file. Relative and absolute paths, environment variables and can be used. |
| scm_tmpdir | Path to the ADF-internal scratch directory. Usually, this is set at installation, but can be overridden here. Should not exist and must not be identical to scratchdir. |
| scratchdir | Is a path to the temporary directory. Relative and absolute paths, environment variables and can be used. If it does not exist, the interface will create it. In any case, the interface will delete this directory after the calculation. |
| savedir | Is a path to another temporary directory. Relative and absolute paths, environment variables and can be used. The interface will store files needed for restart there. |
| memory | The memory usable by WFOVERLAP. The default is 100 MB. The ADF memory usage cannot be controlled. |
| ncpu | The number of CPUs used by the interface. Is overridden by environment variables from queuing engines (e.g., $NSLOTS or $SLURM_NTASKS_PER_NODE). Will either be used to run ADF in parallel or to run several independent ADF runs at the same time. |
| schedule_scaling | Gives the expected parallelizable fraction of the ADF run time (Amdahl’s law). With a value close to zero, the interface will try to run all jobs at the same time. With values close to one, jobs will be run sequentially with the maximum number of cores. |
| delay | Followed by a float giving the delay in seconds between starting parallel jobs to avoid excessive disk I/O (usually not necessary). |
| qmmm_table | Followed by the path to the connection table file, in ADF format. |
| qmmm_ff_file | Followed by the path to the force field file, in Amber95-like format for ADF. |
| neglected_gradient | Decides how not-requested gradients are reported back (Options: zero: default, not-requested gradients are zero; gs: not-requested gradients are equal to ground state gradient; closest: not-requested gradients are equal to closest-energy requested gradient). |
| wfoverlap | Path to the WFOVERLAP code. Needed for overlap and Dyson norm calculations. |
| wfthres | (float) Gives the amount of wave function norm which will be kept in the truncation of the determinant files. Default is 0.99 (i.e., the wave functions in the determinant files will have a norm of 0.99). Note that if hybrid functionals and no TDA are used, the response vector can have a norm larger than one, and wfthres should be increased. |
| numfrozcore | Number of frozen core orbitals for overlap and Dyson norm calculations. A value of -1 enables automatic frozen core. |
| numocc | Number of ignored occupied orbitals in Dyson calculations. |
| nooverlap | Do not save determinant files for overlap computations. |
| theodir | Path to the THEODORE installation. Relative and absolute paths, environment variables and can be used. The interface will set $PYTHONPATH automatically. |
| theodore_prop | Followed by a list with the descriptors which THEODORE should compute. Note that descriptors will only be computed for restricted singlets (and triplets). Instead of a simple list, a Python literal can also be used, as in the THEODORE input files. |
| theodore_fragment | Followed by a list of atom numbers which should constitute a fragment in THEODORE. For multiple fragments, the keyword can be used multiple times. Instead, the keyword can be followed by a Python literal, as in the THEODORE input files. |
| always_orb_init | Do not use the orbital guesses from previous calculations/time steps, but always use the provided initial orbitals. |
| always_guess | Always use the orbital guess from ADF. |
| debug | Increases the verbosity of the interface (standard out). Does not clean up the scratch directory. Copies all ADF outputs to the save directory. |
| no_print | Reduces interface standard output. |
Parallelization
ADF usually shows very good parallel scaling for most calculations.
However, it is more efficient to carry out multiple ADF calculations (different multiplicities, multiple gradients) in parallel, each one using a smaller number of CPUs.
In the SHARC-ADF interface, parallelization is controlled by the keywords ncpu and schedule_scaling.
The first keyword controls the maximum number of CPUs which the interface is allowed to use for all ADF runs simultaneously.
The second keyword is the parallel fraction from Amdahl’s Law, see Section 8.3.
With a value close to zero, the interface will try to run all jobs at the same time. With values close to one, jobs will be run sequentially with the maximum number of cores.
Typical values for schedule_scaling are 0.95 for GGA functionals, 0.75 for hybrid functionals, and 0.90 for hybrid functions in combination with the rihartreefock option.
Note that when using ADF2019 or newer, multiple gradients can be computed in a single ADF run, so that there will be multiple jobs to schedule only if including several multiplicities (beyond singlet plus triplet).
If only a single multiplicity is computed (or singlets plus triplets), then the schedule_scaling keyword does not have any effect.
6.7.3 QM/MM force field file: ADF.qmmm.ff
The force field file for ADF contains all force field parameters for the MM part of the QM/MM calculation.
The interface uses this file without any modification, except that it will copy the file into the relevant scratch directory.
The force field file needs to be in the format specified in the ADF manual, which is similar in format to an AMBER parameter file.
$SHARC/../examples/SHARC_ADF_qmmm/ADF.qmmm.ff contains a functioning example of the file format.
Here, we only show briefly the general format:
FORCE_FIELD_SETTINGS ================================= ELSTAT_1-4_SCALE 0.8333 ELSTAT_NB_CUTOFF none VDW_1-4_SCALE 0.5 VDW_DEFAULT_POTENTIAL 1 (1:6-12 2:exp-6 3:exp purely repulsive) VDW_NB_CUTOFF none DIELECTRIC_CONSTANT 1.000 ================================= MASSES & ATOM LABELS -------------------------------- force_field atomic atom_type symbol mass NOTES ================================ BR Br 79.9000 bromine ================================ BONDS Ebond = 0.5*K(r-ro)**2 -------------------------------- Atoms pot i - j type K R NOTES ============================== C CT 1 634.00 1.522 JCC,7,(1986),230; AA ============================== BENDS Ebend = 0.5*k(a-ao)^2 (K in kcal/mol*rad^2) -------------------------------- Atoms pot i - j - k type K theta NOTES =================================== H1 CT HC 1 70.00 109.50 M. Swart added =================================== TORSIONS Etors=K(1+cos(nt-to)) -------------------------------- Atoms pot per. shift i - j - k - l type k n to NOTES ================================================= * C CT * 1 0.0000 2 0.0 JCC,7,(1986),230 ================================================= OUT-OF-PLANE Etors=K(1-cos(2t-to)) -------------------------------- Atoms pot i - j - k - l type K to NOTES ===================================== * * CC * 1 1.00 180.0 HEME improper ===================================== VAN DER WAALS -------------------------------- atom(s) Emin Rmin gamma NOTES ==================================== H 0.0157 1.2000 12.00 Ferguson base pair geom. ==================================== CHARGES -------------------------------- type charge(e) NOTES ===================== OW -0.8340 Amber95 water charges (TIP3P had -0.82) =====================
6.7.4 QM/MM connection table file: ADF.qmmm.table
The connection table file defines the topology of the QM/MM system, by defining which atoms belong to QM or MM, and which atoms have MM bonds between them.
The file can also be used to define link atoms or to override the MM charges of specific atoms.
In the ADF input file, the interface will automatically add the line MM_CONNECTION_TABLE (so this line should not be present in ADF.qmmm.table), then copy the content of ADF.qmmm.table verbatim to the ADF input, and then add a line END.
Hence, ADF.qmmm.table needs to follow the format required by ADF.
See the ADF manual for details on this input section.
An example of the file is given in $SHARC/../examples/SHARC_ADF_qmmm/ADF.qmmm.table.
In the simplest form, the content of the file could look like:
1 SO QM 2 2 C QM 1 3 4 3 H1 QM 2 4 H1 QM 2 5 OW MM 6 7 6 HW MM 5 7 HW MM 5
Here, the first column is the atom index, the second is the MM atom type (as defined in the force field file), the third column is the atom designation (either QM, MM, or LI for a link atom), and the remaining entries are the atom indices to which the current atom is bonded in MM.
Note that in the connection table, all MM atoms must come at the very end.
As the file content is copied verbatim, it is possible to add further sublocks to the QM/MM input section.
This is necessary if any of the atoms is designated as link atom (label LI).
In this case, the LINK_BONDS section needs to be added:
1 SO QM 2 2 C QM 1 3 4 3 HP QM 2 4 CT QM 2 5 6 7 5 H1 QM 4 6 H1 QM 4 7 CT LI 4 8 9 10 8 HC MM 7 9 HC MM 7 10 HC MM 7 subend link_bonds 7 - 4 1.4 H.1 HC
Note how the MM_CONNECTION_TABLE block is terminated by subend and then the LINK_BONDS section starts; the LINK_BONDS section is not terminated by subend because the interface adds a subend after the file content.
Within the LINK_BONDS section, each line has the following structure: (i) atom index of the LI atom; (ii) a - separated by spaces; (iii) atom index of a QM atom bonded to the link atom; (iv) a floating point number giving the parameter f; (v) the atomic fragment type of the atom which replaces the LI atom in the QM calculation; (vi) the MM atom type of the replacing atom.
Note that for ADF the order of (i) and (iii) does not matter, but it does for the interface, and giving the atom index of the QM atom first will currently lead to an error.
Given these parameters, internally ADF will replace the LI atom by an atom of the specified atomic fragment type, which will be placed on the QM–LI bond where the new bond length is the old bond length divided by f.
The file can also be used to override the MM charges for specific atoms:
1 SO QM 2 2 C QM 1 3 4 3 H1 QM 2 4 H1 QM 2 5 OW MM 6 7 6 HW MM 5 7 HW MM 5 subend charges 5 -0.96 6 +0.48 7 +0.48
The same rules regarding the subend as above apply.
6.7.5 Input file generator: ADF_input.py
In order to quickly setup simple calculations using ADF, the SHARC suite contains a small script called ADF_input.py. It can be used to setup single point calculations, optimizations, and frequency calculations on the DFT and TD-DFT level of theory. Of course, ADF has far more capabilities, but these are not covered by ADF_input.py. For more complicated inputs, users should manually adjust the generated input or employ adfinput.
Note that the script cannot write template files for SHARC_ADF.py.
These templates can better be created by modifying the example template file in $SHARC/../examples/SHARC_ADF/ADF.template.
The script interactively asks the user to specify the calculation and writes an input file and optionally a run script.
Input
Type of calculation
Choose to either perform a single-point calculation or a minimum optimization (including optionally frequency calculation).
The standard output or TAPE21 files from a frequency calculation can be converted (see section 6.7.6) to a file in MOLDEN format, which can then be used to generate initial conditions with wigner.py.
Geometry, Charge, Multiplicity
Specify the geometry file in xyz format. Number of atoms and total nuclear charge is detected automatically. After the user inputs the total charge, the number of electrons is calculated automatically. The number of unpaired electrons can be specified to define the multiplicity.
Basis set
With ADF_input.py it is only possible to enter a single basis set for all atoms. More complicated basis setups can be achieved by manually adjusting the generated input file.
Level of theory
One can setup calculations with any ADF-supported functional, and for ground state or excited state. The user is also queried whether relativistic effects need to be included, and for the most important accuracy settings.
6.7.6 Frequencies converter: ADF_freq.py
The small script ADF_freq.py can be used to convert the standard output or the TAPE21 file created by an ADF frequency calculation.
The usage is very simple:
$SHARC/ADF_freq.py ADF.out
or:
$SHARC/ADF_freq.py TAPE21
The script detects automatically the file format.
Note that in ADF, the infrared intensities are only accessible from the standard output, so use this for IR spectrum generation.
However, the data in TAPE21 has a higher numeric precision, so it is recommended to convert the TAPE21 file if no intensities are needed.
In any case, a file called <filename>.molden is written, containing the frequencies and normal modes.
This file can then be used with wigner.py.
Note that in SHARC2.1, this script was changed to use the KFFile library of ADF, meaning that (like SHARC_ADF.py, you will need ADF2019 or newer and Python 3.5 or higher to run it.
6.8 RICC2 Interface
The SHARC– RICC2 interface can be used to conduct excited-state dynamics based on TURBOMOLE‘s CC2 and ADC(2) methods, for singlet and triplet states.
The interface uses the programs define, dscf and ricc2.
For spin-orbit couplings, ORCA needs to be installed in addition to TURBOMOLE.
Only ADC(2) can be used to calculate spin-orbit couplings, but not CC2 (hence, it is not recommended to perform CC2 calculations with both singlet and triplet states).
Even with ADC(2), only singlet-triplet SOCs are obtained, but no triplet-triplet SOCs; S0-triplet SOCs are also missing currently.
THEODORE (version 2.0 and higher) can be used to perform automatic wave function analysis.
Wavefunction overlaps are calculated using the WFOVERLAP code of the González group.[74]
The SHARC– RICC2 interface furthermore allows to perform QM/MM dynamics (ADC(2) or CC2 plus force fields), using TINKER for the MM part.
The interface needs two additional input files, a template file for the quantum chemistry (file name is RICC2.template) and a general input file (RICC2.resources).
If a file QM/mos.init is are present, it is used to provide an initial orbital guess for the SCF calculation.
In the case of QM/MM calculations, two more input files are needed: an AMBER95 force field file, and RICC2.qmmm.table, which contains the connectivity and force field IDs per atom.
6.8.1 Template file: RICC2.template
This file contains the specifications for the quantum chemistry calculation. Note that this is not a valid TURBOMOLE input file. The file only contains a number of keywords, given in table 6.11. The actual input for TURBOMOLE will be generated automatically through define.
A fully commented template file with all possible options is located in $SHARC/../examples/SHARC_RICC2/.
| Keyword | Description |
| basis | The basis set used. The interface will convert this string to the correct case for TURBOMOLE. |
| auxbasis | The auxiliary basis set used in ricc2. If no auxbasis is given, the interface will let define decide on a suitable auxbasis. |
| basislib | Path to external basis set library. Can be used to employ custom basis sets. |
| charge | The total molecular charge. The interface will calculate the number of electrons automatically during setup. |
| method | Followed by a string, which is either “CC2” or “ADC(2)” (case insensitive), defining the level of theory. Default is “ADC(2)”. |
| douglas-kroll | Activates the use of the scalar-relativistic DK Hamiltonian of 2nd order. Default (if no keyword is given) is to use the non-relativistic Hamiltonian. |
| spin-scaling | Followed by a string, which is either “none”, “scs” or “sos”. Using these options, spin-component scaling can be activated. Under certain restrictions (no SOC, no transition dipole moments, no SMP), “lt-sos” can be used to perform cheaper “sos” calculations. |
| scf | Followed by a string which is either “dscf” or “ridft”. Using this option, the SCF program can be chosen. Note that currently, there is no advantage of using “ridft”. |
| frozen | Followed by an integer giving the number of frozen core orbitals in the ricc2 calculations. Default is to use frozen core orbitals and let define decide on the number. If frozen core is not wanted, use frozen 0 in the template. |
| qmmm | Activates QM/MM with electrostatic embedding. |
External basis set libary
If users want to employ their own basis sets, they can create a basis set library directory with the required files, and use the basislib keyword to tell the interface to use this directory.
The basislib keyword cannot be used together with the auxbasis keyword.
The specified directory must contain basen/ and cbasen/ subdirectories. These must contain one file per element, containing the desired basis set parameters.
The files in cbasen/ must auxiliary basis sets of the same name as the basis sets in basen/.
See the TURBOMOLE directory structure to see how the directories and files need to be prepared.
6.8.2 Resource file: RICC2.resources
The file RICC2.resources contains mainly paths (to the TURBOMOLE and ORCA executables, to the scratch directory, etc.). This file must reside in the same directory where the interface is started. It uses a simple “keyword argument” syntax. Comments using # and blank lines are possible, the order of keywords is arbitrary. Lines with unknown keywords are ignored, since the interface just searches the file for certain keywords.
Table 6.12 lists the existing keywords.
A fully commented resource file with all possible options is located in $SHARC/../examples/SHARC_RICC2/.
| Keyword | Description |
| turbodir | Is the path to the TURBOMOLE installation directory. This directory should contain subdirectories like bin/, basen/, cbasen/, or scripts/. Relative and absolute paths, environment variables and can be used. The interface will set $TURBODIR to this path, and will set the $PATH correctly (using TURBOMOLE‘s sysname tool. If this keyword is not present in RICC2.resources, the interface will use the environment variable $TURBODIR, if it is set. |
| orcadir | Is the path to the ORCA installation, which is necessary when spin-orbit couplings are calculated. Relative and absolute paths, environment variables and can be used. If this keyword is not present in RICC2.resources, the interface will use the environment variable $ORCADIR, if it is set. Note that this seems to work only with ORCA 4 but not with ORCA 5. |
| tinker | The path to the TINKER installation directory. This directory should contain the bin/ subdirectory. |
| scratchdir | Is a path to the temporary directory. Relative and absolute paths, environment variables and can be used. If it does not exist, the interface will create it. In any case, the interface will delete this directory after the calculation. |
| savedir | Is a path to another temporary directory. Relative and absolute paths, environment variables and can be used. The interface will store files needed for restart there. |
| memory | The memory usable by TURBOMOLE and WFOVERLAP. The default is 100 MB. |
| ncpu | The number of CPUs used by the interface. If larger than one, the interface will use the SMP executables of TURBOMOLE with the given number of CPUs. |
| always_orb_init | Do not use the orbital guesses from previous calculations/time steps, but always use the provided initial orbitals. |
| always_guess | Always use the orbital guess from the EHT calculation of define. |
| dipolelevel | Followed by an integer which is either 0, 1, or 2. Controls which dipole moment calculations are skipped by the interface. |
| wfoverlap | Is the path to the WFOVERLAP executable. Relative and absolute paths, environment variables and can be used. This keyword is only necessary if overlaps need to be calculated. |
| wfthres | Threshold for the truncation of the response vectors which are used in the overlap calculations. A threshold of x implies that only the minimal number of determinants needed to give a norm of 1−x are included. |
| numfrozcore | Overrides the number of frozen core orbitals for the overlap calculation. Default is to use the frozen orbitals from the RICC2 steps. |
| nooverlap | Do not save files necessary to do overlaps. |
| debug | Increases the verbosity of the interface. |
| no_print | Reduces interface standard output. |
Note that the interface sets all environment variables necessary to run TURBOMOLE (e.g., $PATH) automatically, based on the input from RICC2.resources and QM.in.
For parallel calculations, the interface will call the SMP executables of TURBOMOLE and WFOVERLAP.
Note that the dipolelevel keyword can have significant impact on the calculation time.
Generally, in response methods like CC2 and ADC(2), extra computational effort is required for the calculation of state and transition dipole moments .
However, dipole moments have only influence in the dynamics simulations if a laser field is present.
Using the dipolelevel keyword, it is possible to deactivate dipole moment calculations if they are not required.
There are three different settings for dipolelevel:
- dipolelevel=0: The interface will return only dipole moments which can be calculated at no cost (state dipole moments of states where a gradient is calculated; excited-excited transition dipole moments if SOCs are calculated)
- dipolelevel=1: In addition, the interface will calculate transition dipole moments between S0 and excited singlet states. Use at least this level for the initial condition setup (setup_init.py takes care of this).
- dipolelevel=2: The interface will calculate all state and transition dipole moments
If only energies and dipole moments are calculated, dipolelevel=1 is only slightly more expensive than dipolelevel=0, while dipolelevel=2 increases computation time more strongly.
However, the computation time also depends on whether or not spin-orbit couplings and gradients are calculated.
6.8.3 QM/MM force field file
These force field files should have the format that can be found in the TINKER directory.
6.8.4 QM/MM connection table file: RICC2.qmmm.table
This file defines which atoms are in the QM or MM region, the atom types (for TINKER), and the connectivity.
Note that the SHARC– RICC2 interface uses newly developed routines to setup QM/MM calculations and communicate with TINKER, so this file is not identical to the table files of the ADF or MOLCAS interfaces (it uses the same routines as the SHARC– ORCA interface).
A sample looks like:
QM 223 QM 222 1 3 4 QM 136 QM 80 MM 63 6 7 MM 64 MM 64
Each line corresponds to one atom.
The example has 7 atoms, the first four in the QM region and the three last ones in the MM region.
The second column defines the atom types according to the numbering in the used force field file.
The integers to the right define the connectivity.
Note that the interface automatically adds any necessary redundancy to the connectivity table, so it is enough in the table file to define a bond once.
6.9 LVC Interface
The purpose of the LVC interface is to allow performing computationally efficient dynamics using a linear vibronic coupling (LVC) model [120].
The relevant equations can be found in section 8.18.
6.9.1 Input files
Two input files are needed:
V0.txt Contains all information to describe V0: the equilibrium geometry, the frequencies ωi, and an orthogonal matrix containing the normal coordinates Kαi.
Geometry S 16. 0.00000000 0.00000000 -0.00039079 31.97207180 O 8. 0.00000000 -2.38362453 1.36159121 15.99491464 O 8. 0.00000000 2.38362453 1.36159120 15.99491464 Frequencies 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00234 0.0053 0.0064 Mass-weighted normal modes 0.0000 1.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.6564 0.0000 0.0000 0.3108 0.0494 0.2004 0.0000 0.0000 -0.6557 ...
V0.txt can be created from a MOLDEN file using wigner.py.
LVC.template Contains the state-specific information: ϵi, κi(n), λj(m,n), ηmn, as well as (transition) dipole moments.
Here, for multiplets ϵi, κi(n), and λj(m,n) are shared between the multiplet components, whereas in the SOC and dipole moment matrices the multiplet components need to be considered explicitly.
V0.txt 4 0 3 epsilon 7 1 1 0.0000000000 1 2 0.1640045037 1 3 0.1781507393 1 4 0.2500917150 3 1 0.1341247878 3 2 0.1645714941 3 3 0.1700512159 kappa 12 1 2 7 1.19647e-03 1 2 8 1.21848e-02 ... lambda 3 1 1 4 9 -1.83185e-02 1 2 3 9 7.32022e-03 3 1 3 9 5.71746e-03 SOC R 0.000e+00 0.000e+00 0.000e+00 0.000e+00 0.000e+00 0.000e+00 ... 0.000e+00 0.000e+00 0.000e+00 0.000e+00 0.000e+00 -1.086e-04 ... ... SOC I 0.000e+00 0.000e+00 0.000e+00 0.000e+00 0.000e+00 0.000e+00 ... 0.000e+00 0.000e+00 0.000e+00 1.000e+00 0.000e+00 1.000e-04 ... ... DMX R -7.400e-07 -1.639e-01 0.000e+00 3.000e-06 0.000e+00 0.000e+00 ... -1.639e-01 3.930e-06 0.000e+00 2.400e-05 0.000e+00 0.000e+00 ... ... DMX I ... DMY R ... DMY I ... DMZ R ... DMZ I ...
Only the two first lines are mandatory, but then all states will have the same potentials (the ground state potential).
6.9.2 Template File Setup: wigner.py, setup_LVCparam.py, and create_LVCparam.py
Reference potential
V0.txt is created using the wigner.py script, which is also used for initial condition generation. Simply call, e.g.
$SHARC/wigner.py -l <filename.molden>
Note that this best works if all 3N normal modes are present in the file. If the translations and rotations are missing, the script will add the necessary number of zero-vector modes.
Setup for single point calculations
To obtain the LVC parameters, two steps are necessary: (i) running quantum chemistry calculations, and (ii) converting the quantum chemistry output to the LVC parameters.
The first of these steps is carried out with setup_LVCparam.py.
It is an interactive script that works very similarly to the other setup scripts (e.g., setup_init.py, setup_traj.py).
The script will ask for the following:
- Path to the V0.txt file,
- Number of states,
- Which interface to use (in principle, all SHARC-interfaces can be used, but only the ab initio interfaces are useful here),
- Whether spin-orbit couplings should be calculated (only if applicable),
- Whether κ parameters should be obtained from analytical gradients or numerical differentiation (depends on availability of analytical gradients),
- Whether λ parameters should be obtained from analytical nonadiabatic coupling vectors or numerical differentiation (depends on availability of analytical nonadiabatic coupling vectors),
- Which normal modes to include,
- Which displacement value to use for numerical differentiation (default 0.05 dimensionless mass-frequency scaled units),
- Whether intruder states should be ignored or not,
- Whether one- or two-sided differentiation should be done,
- Interface-specific input for the chosen quantum chemistry interface (see section 7.5.3).
The script will set up a directory (DSPL_RESULTS) with one subdirectory for each single point calculation.
If both κ’s and λ’s are computed analytically, then only the DSPL_000_eq subdirectory will be present.
Otherwise, for each chosen normal mode 1-2 subdirectories (for one-sided or two-sided differentiation) will be present.
Additionally, displacements.log presents the most important settings.
In all cases, displacements.json is also present; this file is crucial to communicate all settings to the read-out script after the single point jobs are finished.
Extracting LVC parameters
After all jobs are successfully finished (QM.out file present in each directory), run create_LVCparam.py inside the DSPL_RESULTS directory.
This is a fully automatic script that reads displacements.json and the QM.out files in the subdirectories.
After everything is successfully read, it creates the LVC.template file.
This file can be used to run SHARC-LVC trajectories.
6.10 GAUSSIAN Interface
The SHARC– GAUSSIAN interface allows to run SHARC simulations with GAUSSIAN‘s TD-DFT functionality.
The interface is compatible with restricted and unrestricted ground states, but not with symmetry.
Spin-orbit couplings cannot be computed, but wave function overlaps from the WFOVERLAP code are available (no nonadiabatic couplings).
Dyson norms can also be computed through the WFOVERLAP code.
THEODORE (version 2.0 or higher) can be used to perform automatic wave function analysis.
The interface needs two additional input files, a template file for the quantum chemistry (file name is GAUSSIAN.template) and a resource file (GAUSSIAN.resources).
If files QM/GAUSSIAN.chk.init or QM/GAUSSIAN.chk.<job>.init are present, they are used to provide an initial orbital guess for the SCF calculation of the respective job.
6.10.1 Template file: GAUSSIAN.template
This file contains the specifications for the quantum chemistry calculation. Note that this is not a valid GAUSSIAN input file. The file only contains a number of keywords, given in table 6.13. The actual input for GAUSSIAN will be generated automatically through the interface.
A fully commented template file-with all possible options, a comprehensive descriptions, and some practical hints-is located in $SHARC/../examples/SHARC_GAUSSIAN/GAUSSIAN.template.
We recommend that users start from this template file and modify it appropriately for their calculations.
| Keyword | Description |
| basis | Gives the basis set for all atoms (default 6-31G). |
| functional | followed by one string giving the exchange-correlation functional. Default is PBEPBE. |
| dispersion | Activates dispersion correction. Arguments are written verbatim to GAUSSIAN input (in EmpiricalDispersion=()). Default is no dispersion. An example argument would be GD3. |
| charge | Sets the total charge of the system. Can be either followed by a single integer (then the interface will automatically assign the charges to the multiplicities) or by one charge per multiplicity. |
| scrf | Activates solvation. All arguments (e.g., iefpcm solvent=water) are copied to GAUSSIAN input (in scrf=()). |
| grid | Followed by a string (e.g., grid finegrid) defining which integration grid and accuracy to use. For details, see the example template file. |
| denfit | Activates density fitting, which might speed up the computation. |
| scf | Arguments are written verbatim to GAUSSIAN input (in scf=()). |
| no_tda | This keyword deactivates TDA, which the interface requests by default. |
| paddingstates | Followed by a list of integers, which give the number of extra states to compute by GAUSSIAN, but which are neglected in the output. Should not be changed between time steps, as this will break GAUSSIAN‘s restart routines. |
| unrestricted_triplets | Requests that the triplets are calculated in a separate job from an unrestricted ground state. Default is to compute triplets as linear response of the restricted singlet ground state. |
| iop | Arguments are written verbatim to GAUSSIAN input (in iop=()). Expert option. |
| keys | Arguments are written verbatim to GAUSSIAN input as separate keywords. Expert option. |
6.10.2 Resource file: GAUSSIAN.resources
The file GAUSSIAN.resources contains mainly paths (to the GAUSSIAN executables, to the scratch directory, etc.) and other resources, plus settings for wfoverlap.x and THEODORE. This file must reside in the same directory where the interface is started. It uses a simple “keyword argument” syntax. Comments using # and blank lines are possible, the order of keywords is arbitrary. Lines with unknown keywords are ignored, since the interface just searches the file for certain keywords.
Table 6.14 lists the existing keywords.
A fully commented resource file with all possible options and comprehensive descriptions is located in $SHARC/../examples/SHARC_GAUSSIAN/.
| Keyword | Description |
| groot | Is the path to the GAUSSIAN installation directory. This directory should contain the GAUSSIAN executables, e.g., g09/g16, l9999.exe, etc. Relative and absolute paths, environment variables and can be used. The interface will set $GAUSS_EXEDIR to this path. |
| scratchdir | Is a path to the temporary directory. Relative and absolute paths, environment variables and can be used. If it does not exist, the interface will create it. In any case, the interface will delete this directory after the calculation. The interface will set $GAUSS_SCRDIR to this path. |
| savedir | Is a path to another temporary directory. Relative and absolute paths, environment variables and can be used. The interface will store files needed for restart there. |
| memory | The memory usable by GAUSSIAN and WFOVERLAP. The default is 100 MB. |
| ncpu | The number of CPUs used by the interface. Is overridden by environment variables from queuing engines (e.g., $NSLOTS or $SLURM_NTASKS_PER_NODE). Will either be used to run GAUSSIAN in parallel or to run several independent GAUSSIAN runs at the same time. |
| schedule_scaling | Gives the expected parallelizable fraction of the GAUSSIAN run time (Amdahl’s law). With a value close to zero, the interface will try to run all jobs at the same time. With values close to one, jobs will be run sequentially with the maximum number of cores. |
| delay | Followed by a float giving the delay in seconds between starting parallel jobs to avoid excessive disk I/O (usually not necessary). |
| wfoverlap | Path to the WFOVERLAP code. Needed for overlap and Dyson norm calculations. |
| wfthres | (float) Gives the amount of wave function norm which will be kept in the truncation of the determinant files. Default is 0.99 (i.e., the wave functions in the determinant files will have a norm of 0.99). Note that if hybrid functionals and no TDA are used, the response vector can have a norm larger than one, and wfthres should be increased. |
| numfrozcore | Number of frozen core orbitals for overlap and Dyson norm calculations. A value of -1 enables automatic frozen core. |
| numocc | Number of ignored occupied orbitals in Dyson calculations. |
| nooverlap | Do not save determinant files for overlap computations. |
| theodir | Path to the THEODORE installation. Relative and absolute paths, environment variables and can be used. The interface will set $PYTHONPATH automatically. |
| theodore_prop | Followed by a list with the descriptors which THEODORE should compute. Note that descriptors will only be computed for restricted singlets (and triplets). Instead of a simple list, a Python literal can also be used, as in the THEODORE input files. |
| theodore_fragment | Followed by a list of atom numbers which should constitute a fragment in THEODORE. For multiple fragments, the keyword can be used multiple times. Instead, the keyword can be followed by a Python literal, as in the THEODORE input files. |
| always_orb_init | Do not use the orbital guesses from previous calculations/time steps, but always use the provided initial orbitals. |
| always_guess | Always use the orbital guess from GAUSSIAN. |
| debug | Increases the verbosity of the interface (standard out). Does not clean up the scratch directory. Copies all GAUSSIAN outputs to the save directory. |
| no_print | Reduces interface standard output. |
Parallelization
GAUSSIAN usually shows very good parallel scaling for most TD-DFT calculations.
However, it is more efficient to carry out multiple GAUSSIAN calculations (different multiplicities, multiple gradients) in parallel, each one using a smaller number of CPUs.
In the SHARC– GAUSSIAN interface, parallelization is controlled by the keywords ncpu and schedule_scaling.
The first keyword controls the maximum number of CPUs which the interface is allowed to use for all GAUSSIAN runs simultaneously.
The second keyword is the parallel fraction from Amdahl’s Law, see Section 8.3.
With a value close to zero, the interface will try to run all jobs at the same time. With values close to one, jobs will be run sequentially with the maximum number of cores.
Typical values for schedule_scaling are around 0.90 for both GGA functionals and hybrid functionals, possibly less for very small computations.
6.11 ORCA Interface
The SHARC– ORCA interface allows to run SHARC simulations with ORCA‘s TD-DFT functionality.
The interface is compatible with restricted and unrestricted ground states, but not with symmetry.
Spin-orbit couplings can be computed and wave function overlaps from the WFOVERLAP code are available (no nonadiabatic couplings).
Dyson norms can also be computed through the WFOVERLAP code.
THEODORE (version 2.0 or higher) can be used to perform automatic wave function analysis.
Note that the interface only works with ORCA 4.1, 4.2, and 5 (you can check by looking whether the program orca_fragovl is present in the ORCA installation).
The SHARC– ORCA interface furthermore allows to perform QM/MM dynamics (TDDFT plus force fields), using TINKER for the MM part.
The interface needs two additional input files, a template file for the quantum chemistry (file name is ORCA.template) and a resource file (ORCA.resources).
If files QM/ORCA.gbw.init or QM/ORCA.gbw.<job>.init are present, they are used to provide an initial orbital guess for the SCF calculation of the respective job.
In the case of QM/MM calculations, two more input files are needed: an AMBER95 force field file, and ORCA.qmmm.table, which contains the connectivity and force field IDs per atom.
6.11.1 Template file: ORCA.template
This file contains the specifications for the quantum chemistry calculation. Note that this is not a valid ORCA input file. The file only contains a number of keywords, given in table 6.15. The actual input for ORCA will be generated automatically through the interface.
A fully commented template file-with all possible options, a comprehensive descriptions, and some practical hints-is located at $SHARC/../examples/SHARC_ORCA/ORCA.template.
For QM/MM calculations, a second example template (along with the QM/MM-specific files) is located at $SHARC/../examples/SHARC_ORCA_Tinker/ORCA.template.
We recommend that users start from this template file and modify it appropriately for their calculations.
Note that for ORCA 4.2, when doing TD-DFT gradient calculations with hybrid functions, it might be necessary to add a “/C” basis set.
While there is no special keyword in ORCA.template for this basis set, it can be specified with the general key keyword.
| Keyword | Description |
| basis | Gives the basis set for all atoms (default 6-31G). |
| auxbasis | Gives the auxiliary basis set (default: Orca chooses). |
| basis_per_element | Overrides the basis set for the specified element (argument 1: element symbol, argument 2: basis set). Can be given multiple times. |
| basis_per_atom | Overrides the basis set for the specified atom (argument 1: atom number starting at 1 and only counting QM atoms, argument 2: basis set). Can be given multiple times. |
| functional | followed by one string giving the exchange-correlation functional. Default is PBE. |
| hfexchange | Modifies the amount of HF exchange in the functional (give in fraction of 1). Default is whatever the chosen functional uses. |
| dispersion | Activates dispersion correction. Arguments are written verbatim to ORCA input (in EmpiricalDispersion=()). Default is no dispersion. An example argument would be GD3. |
| range_sep_settings | Controls several functional parameters. Is followed by 5 arguments: RangeSepMu, RangeSepScal, ACM-A, ACM-B, ACM-C. Each is a floating point number. See the ORCA manual for details on these settings. Note that ACM-A should not be used together with hfexchange. |
| charge | Sets the total charge of the system. Can be either followed by a single integer (then the interface will automatically assign the charges to the multiplicities) or by one charge per multiplicity. |
| grid | Followed by a number (e.g., grid 4) defining which integration grid and accuracy to use. For details, see the example template file. Do not use this keyword with ORCA 5. |
| gridx | To control the exchange grid (rijcosx). Do not use this keyword with ORCA 5. |
| gridxc | To control the exchange-correlation grid (TDDFT). Do not use this keyword with ORCA 5. |
| ri | Controls the density fitting scheme. Arguments can be, e.g., rijcosx. If not given, RI is deactivated. |
| keys | Arguments are written verbatim to ORCA input as separate keywords. Expert option. Note that this can be used to do PCM calculations (but requesting gradients will lead to a crash). With ORCA 5, you can put grid-related keywords here. |
| no_tda | This keyword deactivates TDA, which the interface requests by default. |
| paddingstates | Followed by a list of integers, which give the number of extra states to compute by GAUSSIAN, but which are neglected in the output. Should not be changed between time steps, as this will break GAUSSIAN‘s restart routines. |
| unrestricted_triplets | Requests that the triplets are calculated in a separate job from an unrestricted ground state. Default is to compute triplets as linear response of the restricted singlet ground state. |
| qmmm | Activates QM/MM. In this case, the interface will look for two additional input files (see below). |
6.11.2 Resource file: ORCA.resources
The file ORCA.resources contains mainly paths (to the ORCA executables, to the scratch directory, etc.) and other resources, plus settings for wfoverlap.x and THEODORE. This file must reside in the same directory where the interface is started. It uses a simple “keyword argument” syntax. Comments using # and blank lines are possible, the order of keywords is arbitrary. Lines with unknown keywords are ignored, since the interface just searches the file for certain keywords.
Table 6.16 lists the existing keywords.
A fully commented resource file with all possible options and comprehensive descriptions is located in $SHARC/../examples/SHARC_ORCA/.
| Keyword | Description |
| orcadir | Is the path to the ORCA installation directory. This directory should contain executables like orca, orca_int, or orca_fragovl. Relative and absolute paths, environment variables and can be used. The interface will automatically update the $LD_LIBRARY_PATH. |
| tinker | The path to the TINKER installation directory. This directory should contain the bin/ subdirectory. |
| scratchdir | Is a path to the temporary directory. Relative and absolute paths, environment variables and can be used. If it does not exist, the interface will create it. In any case, the interface will delete this directory after the calculation. |
| savedir | Is a path to another temporary directory. Relative and absolute paths, environment variables and can be used. The interface will store files needed for restart there. |
| memory | The memory usable by ORCA and WFOVERLAP. The default is 100 MB. |
| ncpu | The number of CPUs used by the interface. Is overridden by environment variables from queuing engines (e.g., $NSLOTS or $SLURM_NTASKS_PER_NODE). Will either be used to run ORCA in parallel or to run several independent ORCA runs at the same time. |
| schedule_scaling | Gives the expected parallelizable fraction of the ORCA run time (Amdahl’s law). With a value close to zero, the interface will try to run all jobs at the same time. With values close to one, jobs will be run sequentially with the maximum number of cores. |
| delay | Followed by a float giving the delay in seconds between starting parallel jobs to avoid excessive disk I/O (usually not necessary). |
| wfoverlap | Path to the WFOVERLAP code. Needed for overlap and Dyson norm calculations. |
| wfthres | (float) Gives the amount of wave function norm which will be kept in the truncation of the determinant files. Default is 0.99 (i.e., the wave functions in the determinant files will have a norm of 0.99). Note that if hybrid functionals and no TDA are used, the response vector can have a norm larger than one, and wfthres should be increased. |
| numfrozcore | Number of frozen core orbitals for overlap and Dyson norm calculations. A value of -1 enables automatic frozen core. |
| numocc | Number of ignored occupied orbitals in Dyson calculations. |
| nooverlap | Do not save determinant files for overlap computations. |
| theodir | Path to the THEODORE installation. Relative and absolute paths, environment variables and can be used. The interface will set $PYTHONPATH automatically. |
| theodore_prop | Followed by a list with the descriptors which THEODORE should compute. Note that descriptors will only be computed for restricted singlets (and triplets). Instead of a simple list, a Python literal can also be used, as in the THEODORE input files. |
| theodore_fragment | Followed by a list of atom numbers which should constitute a fragment in THEODORE. For multiple fragments, the keyword can be used multiple times. Instead, the keyword can be followed by a Python literal, as in the THEODORE input files. |
| always_orb_init | Do not use the orbital guesses from previous calculations/time steps, but always use the provided initial orbitals. |
| always_guess | Always use the orbital guess from ORCA. |
| debug | Increases the verbosity of the interface (standard out). Does not clean up the scratch directory. Copies all ORCA outputs to the save directory. |
| no_print | Reduces interface standard output. |
| qmmm_table | Followed by the path to the connection table file, in SHARC-QM/MM format. |
| qmmm_ff_file | Followed by the path to the force field file, in AMBER95 format for TINKER. |
| neglected_gradient | Decides how not-requested gradients are reported back (Options: zero: default, not-requested gradients are zero; gs: not-requested gradients are equal to ground state gradient; closest: not-requested gradients are equal to closest-energy requested gradient). |
Parallelization
ORCA usually shows very good parallel scaling for most TD-DFT calculations.
However, it is more efficient to carry out multiple ORCA calculations (different multiplicities) in parallel, each one using a smaller number of CPUs.
Note that ORCA 4.1 can compute multiple gradients in one job, so multiple gradients do not induce multiple jobs.
In the SHARC– ORCA interface, parallelization is controlled by the keywords ncpu and schedule_scaling.
The first keyword controls the maximum number of CPUs which the interface is allowed to use for all ORCA runs simultaneously.
The second keyword is the parallel fraction from Amdahl’s Law, see Section 8.3.
With a value close to zero, the interface will try to run all jobs at the same time. With values close to one, jobs will be run sequentially with the maximum number of cores.
Typical values for schedule_scaling are around 0.90 for both GGA functionals and hybrid functionals, possibly less for very small computations.
6.11.3 QM/MM force field file
These force field files should have the format that can be found in the TINKER directory.
6.11.4 QM/MM connection table file: ORCA.qmmm.table
This file defines which atoms are in the QM or MM region, the atom types (for TINKER), and the connectivity.
Note that the SHARC– ORCA interface uses newly developed routines to setup QM/MM calculations and communicate with TINKER, so this file is not identical to the table files of the ADF or MOLCAS interfaces.
A sample looks like:
QM 223 QM 222 1 3 4 QM 136 QM 80 MM 63 6 7 MM 64 MM 64
Each line corresponds to one atom.
The example has 7 atoms, the first four in the QM region and the three last ones in the MM region.
The second column defines the atom types according to the numbering in the used force field file.
The integers to the right define the connectivity.
Note that the interface automatically adds any necessary redundancy to the connectivity table, so it is enough in the table file to define a bond once.
6.12 BAGEL Interface
The SHARC– BAGEL interface allows to run SHARC simulations with BAGEL‘s CASSCF, SS-CASPT2, MS-CASPT2, and XMS-CASPT2 functionalities.
The interface is compatible with all multiplicities, but not with symmetry.
Note that separate active spaces are used for each multiplicity.
BAGEL features analytical gradients and nonadiabatic couplings for all of these methods, but no spin-orbit coupings.
Wave function overlaps and Dyson norms can be obtained from the WFOVERLAP code.
Note that BAGEL does not allow extracting the AO overlap matrix that is required for overlap and Dyson norm calculations; hence, the SHARC– BAGEL interface computes the AO overlaps through the open-source quantum chemistry code PYQUANTE.
Also note that, currently, it is not recommended to work with MS-CASPT2 gradients and XMS-CASPT2 should always be preferred.
The interface needs two additional input files, a template file for the quantum chemistry (file name is BAGEL.template) and a resource file (BAGEL.resources).
If files QM/archive.<mult>.init are present, they are used to provide an initial orbital guess for the CASSCF calculation of the respective multiplicity.
Note that when running BAGEL, it might be necessary for the user to set $LD_LIBRARY_PATH appropriately, so that all relevant libraries (boost, fabric, …) can be found.
6.12.1 Template file: BAGEL.template
This file contains the specifications for the quantum chemistry calculation. Note that this is not a valid BAGEL input file. The file only contains a number of keywords, given in table 6.17. The actual input for BAGEL will be generated automatically through the interface.
A fully commented template file-with all possible options, a comprehensive descriptions, and some practical hints-is located at $SHARC/../examples/SHARC_BAGEL/BAGEL.template.
For QM/MM calculations, a second example template (along with the QM/MM-specific files) is located at $SHARC/../examples/SHARC_BAGEL_Tinker/BAGEL.template.
We recommend that users start from this template file and modify it appropriately for their calculations.
| Keyword | Description |
| basis | Gives the basis set for all atoms (default svp). It is advisable to always specify a basis set file with absolute path. |
| df_basis | Gives the auxiliary basis set (default: svp-jkfit). It is advisable to always specify a DF basis set file with absolute path. |
| dkh | Activates the (scalar-relativistic) Douglas-Kroll-Hess Hamiltonian. |
| nact | Number of active orbitals. |
| nclosed | Number of closed-shell orbitals. |
| nstate | Number of state-averaging states per multiplicity. |
| method | Can be casscf, caspt2, ms-caspt2, or xms-caspt2. |
| shift | Level shift for CASPT2 (default: 0.0, give float in Hartree). |
| shift_imag | Switches from real to imaginary level shift (use shift to specify the magnitude). |
| orthogonal_basis | Switches on the orthogonal_basis option of BAGEL. Is activated automatically for imaginary level shifts. |
| msmr | Switches on multi-state-multi-reference treatment in CASPT2. Default is single-state-single-reference (SS-SR). |
| maxiter | Iteration limit for energy calculations (SCF, PT2). Default 500. A too high value can slow down the calculation unnecessarily. |
| maxziter | Iteration limit for Z-vector calculations (gradients, NACME). Default 100. A too high value can slow down the calculation unnecessarily. |
| charge | Sets the total charge of the system. Can be either followed by a single integer (then the interface will automatically assign the charges to the multiplicities) or by one charge per multiplicity. |
| frozen | Number of frozen core orbitals for CASPT2 steps. Default is -1, which lets BAGEL automatically decide. |
6.12.2 Resource file: BAGEL.resources
The file BAGEL.resources contains mainly paths (to the BAGEL executables, to the scratch directory, etc.) and other resources, plus settings relevant for wfoverlap.x. This file must reside in the same directory where the interface is started. It uses a simple “keyword argument” syntax. Comments using # and blank lines are possible, the order of keywords is arbitrary. Lines with unknown keywords are ignored, since the interface just searches the file for certain keywords.
Table 6.18 lists the existing keywords.
A fully commented resource file with all possible options and comprehensive descriptions is located in $SHARC/../examples/SHARC_BAGEL/.
| Keyword | Description |
| bagel | Is the path to the BAGEL installation directory. This directory should contain subdirectories bin/ and lib/. Relative and absolute paths, environment variables and can be used. The interface will automatically update the $LD_LIBRARY_PATH. |
| scratchdir | Is a path to the temporary directory. Relative and absolute paths, environment variables and can be used. If it does not exist, the interface will create it. In any case, the interface will delete this directory after the calculation. |
| savedir | Is a path to another temporary directory. Relative and absolute paths, environment variables and can be used. The interface will store files needed for restart there. |
| pyquante | Path to the PYQUANTE installation directory. This directory should contain the PyQuante/ subdirectory that can be imported by Python as a module. Required for overlap and Dyson calculations. |
| memory | The memory usable by WFOVERLAP. The default is 100 MB. Note that the memory for BAGEL cannot be controlled. |
| ncpu | The number of CPUs used by the interface. Is overridden by environment variables from queuing engines (e.g., $NSLOTS or $SLURM_NTASKS_PER_NODE). Will either be used to run BAGEL in parallel or to run several independent BAGEL runs at the same time. |
| schedule_scaling | Gives the expected parallelizable fraction of the BAGEL run time (Amdahl’s law). With a value close to zero, the interface will try to run all jobs at the same time. With values close to one, jobs will be run sequentially with the maximum number of cores. |
| mpi_parallel | If given, the interface will call BAGEL with mpirun -n NCPU, otherwise it will use OpenMP. |
| delay | Followed by a float giving the delay in seconds between starting parallel jobs to avoid excessive disk I/O (usually not necessary). |
| wfoverlap | Path to the WFOVERLAP code. Needed for overlap and Dyson norm calculations. |
| numfrozcore | Number of frozen core orbitals for overlap and Dyson norm calculations. A value of -1 enables automatic frozen core. |
| numocc | Number of ignored occupied orbitals in Dyson calculations. |
| nooverlap | Do not save determinant files for overlap computations. |
| dipolelevel | Followed by an integer which is either 0, 1, or 2. Controls which dipole moment calculations are skipped by the interface. |
| always_orb_init | Do not use the orbital guesses from previous calculations/time steps, but always use the provided initial orbitals. |
| always_guess | Always use the orbital guess from BAGEL. |
| debug | Increases the verbosity of the interface (standard out). Does not clean up the scratch directory. Copies all BAGEL outputs to the save directory. |
| no_print | Reduces interface standard output. |
Note that the dipolelevel keyword can have significant impact on the calculation time.
Generally, in CASPT2 calculations, extra computational effort is required for the calculation of state and transition dipole moments .
However, dipole moments have only influence in the dynamics simulations if a laser field is present.
Using the dipolelevel keyword, it is possible to deactivate dipole moment calculations if they are not required.
There are three different settings for dipolelevel:
- dipolelevel=0: The interface will return only dipole moments which can be calculated at no cost (state dipole moments of states where a gradient is calculated; transition dipole moments if nonadiabatic couplings are calculated)
- dipolelevel=1: In addition, the interface will calculate transition dipole moments between S0 and excited singlet states. Use at least this level for the initial condition setup (setup_init.py takes care of this).
- dipolelevel=2: The interface will calculate all state and transition dipole moments
If only energies and dipole moments are calculated, dipolelevel=1 is only slightly more expensive than dipolelevel=0, while dipolelevel=2 increases computation time more strongly.
However, the computation time also depends on whether or not nonadiabatic couplings and gradients are calculated.
Parallelization
The parallel scaling behavior of BAGEL heavily depends on the system (number of atoms, active space, frozen core, …) and on the parallelization mode (MPI or OpenMP).
Hence, it is advisable that the optimal settings (number of cores, parallelization mode) are tested before starting dynamics projects.
Note that the interface can only trivially parallelize BAGEL calculations across several independent multiplicities, but not across multiple gradient or nonadiabatic coupling calculations.
6.13 The WFOVERLAP Program
This section does not describe an interface to SHARC, but rather the WFOVERLAP program.
This program is part of the SHARC distribution, but can also be obtained as a stand-alone package (including a more detailed manual and a set of auxiliary scripts).
It computes overlaps between many-electron wave functions expressed in terms of linear combinations of Slater determinant, which are based on molecular orbitals (from an LCAO ansatz).
It can also compute Dyson orbitals and Dyson norms between wave functions differing by one α or one β electron.
The program is based on the efficient and general algorithm published in Ref. [74].
It is possible to vary the geometry, the basis set, the molecular orbitals, and the wavefunction expansion between the calculations.
The resulting wave function overlaps or Dyson norms can be used for example for:
- Propagation in local diabatization, the main application inside SHARC,
- Computation of photoionization spectra [31,[87],
- Comparison of wave functions at different levels of theory [88].
If you employ the wfoverlap.x code inside the SHARC suite for these purposes, please cite these references!
The documentation here only gives a brief overview over the input options of WFOVERLAP.X, because within the SHARC suite the wfoverlap.x program is always called automatically by the interfaces. For the full manual (and for access to the auxiliary scripts of WFOVERLAP.X), please download the separate WFOVERLAP package.
6.13.1 Installation
Using precompiled binaries
After unpacking, the directory $SHARC should contain a binary wfoverlap_ascii.x and a link called wfoverlap.x pointing to the binary.
With this setup, most interfaces should work without problems.
Manual installation
The only exceptions are the following: COLUMBUS (overlaps and Dyson norms) and MOLCAS (only Dyson norms).
These features are only available if wfoverlap.x is recompiled with proper support for these programs.
Alternatively, you may want to link wfoverlap.x against your favorite libraries.
In these cases, a manual installation is necessary.
For the manual installation you need a working Fortran90 compatible compiler (Intel’s ifort is recommended),
some reasonably fast BLAS/LAPACK libraries (Intel’s MKL is recommended, although atlas is also fine).
Optionally, with a working COLUMBUS Installation you can install the COLUMBUS bindings, which will
allow direct reading of SIFS integral files generated by DALTON. To use this option, it is
necessary to use the read_dalton.o object file.
MOLCAS/SEWARD integral files can be read by linking with the COLUMBUS/MOLCAS interface. Link against
read_molcas.o for this purpose.
To compile the source code, switch to the source directory and edit the Makefile to adjust it to your Fortran compiler and BLAS/LAPACK installation. The location of your COLUMBUS installation has to be set via the enviroment variable
$COLUMBUS.
Issuing the command:
cd $SHARC/../wfoverlap/source/
make
will compile the source and create the binaries.
If you are unable to link against COLUMBUS and/or MOLCAS, simply call
make wfoverlap_ascii.x
to compile a minimal version of the CI Overlap program that only reads ASCII files.
In this case, overlap and Dyson calculations with SHARC_COLUMBUS.py and Dyson calculations with SHARC_MOLCAS.py will not be possible.
Testing
The command
make test
will run a couple of tests to check if the program is working correctly (alternatively you can call ovl_test.bash $OVDIR, but $OVDIR needs to be set before).
6.13.2 Workflow
The workflow of the overlap program is shown in Figure 6.3.
Four pieces of input, as shown on top, have to be given:
- Overlaps between the two sets of AOs used to construct the bra and ket wavefunctions,
- MO coefficients of the bra and ket wavefunctions,
- information about the Slater determinants,
- the corresponding CI coefficients.
Two main intermediates are computed, the MO overlaps and the unique factors Skl, ―Skl where the latter may require significant amounts of memory to be stored.
The reuse of these intermediates is one of the main reasons for the decent performance of the wfoverlap. program.
6.13.3 Calling the program
The main program is called in the following form
wfoverlap.x [-m <mem=1000>] [-f <input_file=cioverlap.input>]
with the command line options
- -m : amount of memory in MB
- -f : input file
Example:
wfoverlap.x -m 2000 -f wfov.in
Mode
The program automatically detects whether overlaps or Dyson orbitals should be calculated.
If the number of electrons in the bra and ket wavefunctions is the same, wavefunction overlaps are computed.
If the number of α electrons or the number of β electrons differ by exactly 1, Dyson orbitals are computed.
If the wave functions differ by more than one electron, the program will stop with an error message.
Memory
The amount of memory given is a decisive factor for the performance of the code.
Depending on the amount of memory, one of three different modes is chosen:
(i) All Skl and ―Skl terms are kept in core (using arrays called P_ovland Q_ovl).
(ii) Only the Skl factors (P_ovl) are kept in core. This is indicated by
Allocation of Q block overlap matrix failed.
- Using on-the-fly algorithm for Q determinants.
This mode is generally as efficient as 1. but shows somewhat worse parallel scaling.
(iii) Not even all Skl factors can be stored
Only 437 out of 886 columns of the P_ovl matrix are stored in memory (3 MB)!
Increase the amount of memory to improve the efficiency.
This mode is significantly slower than (i) and (ii) and should be avoided by increasing the amount of memory.
Input file
| Keyword | Default | Description |
| a_mo | – | MO coefficient file (bra) |
| b_mo | – | MO coefficient file (ket) |
| a_mo_read | 0 | Format for the MO coefficients (bra): |
| 0: COLUMBUS, 1: MOLCAS, 2: TURBOMOLE | ||
| b_mo_read | 0 | Format for the MO coefficients (ket) |
| a_det | – | Determinant file (bra) |
| b_det | – | Determinant file (ket) |
| ncore | 0 | Number of discarded core orbitals |
| ndocc | 0 | Number of doubly occupied orbitals that are not used for annihilation in Dyson orbital calculations (only has effect if larger than ncore) |
| ao_read | 0 | Format for overlap integrals: |
| 0: ASCII, 1: MOLCAS, 2: COLUMBUS/SIFS, | ||
| -1: Compute by inversion of MO coefficient matrx | ||
| mix_aoovl | S_mix/ONEINT/aoints | AO overlap file |
| for ao_read=0/1/2 | ||
| same_aos | .false. | If both calculations were performed with the same set of AOs (specify only for ao_read=1/2) |
| nao_a | automatic | Number of bra AOs for ao_read=1/2 (specify only if different from ket AOs) |
| nao_b | automatic | Number of ket AOs (see above) |
| moprint | 0 | Print Dyson orbitals: 1: coefficients to std. out, |
| 2: as Jmol script | ||
| force_direct_dets | .false. | Compute Skl terms directly (turn off ßuperblocks”). Recommended if the number of CPU-cores is large (on the same order as the number of ßuperblocks”). |
| force_noprecalc | .false. | Do not precalculate the ―Skl factors. |
| mixing_angles | .false. | Compute mixing angles as a matrix logarithm. |
An example input file is shown below:
a_mo=mocoef_a b_mo=mocoef_b a_det=dets_a b_det=dets_b ao_read=2 same_aos
The full list of keywords is given in Table 6.19.
6.13.4 Input data
Typically, three types of input need to be provided: AO overlaps, MO coefficients, and a combined file with determinant information and CI coefficients (cf. Figure 6.3).
The file formats are explained here.
Within SHARC, these files are automatically extracted or converted by the interfaces, so the user does not need to create them.
AO overlaps
The mixed AO overlaps < χμ|χν′ > between the AOs used to expand the bra and ket wavefunctions are required.
They are in general created by a “double molecule” calculation, i.e. an AO integral calculation where every atom is found twice in the input file.
The native format (ao_read=0) is a simple ASCII file containing the relevant off-diagonal block of the mixed AO overlap matrix, e.g.
7 7 9.97108464676133E-001 2.36720699813181E-001 ... 2.36720699813181E-001 9.99919192433940E-001 ... 1.00147985713321E-002 6.52340422397770E-003 ... ...
In addition, MOLCAS (ao_read=1) and COLUMBUS/SIFS (ao_read=2) files can be read in binary form.
If the same AOs are used for the bra and ket wavefunctions and the MO coefficient matrix is square, it is possible to reconstruct the overlaps by inversion of the MO coefficient matrix (ao_read=-1).
In this case it is not necessary to supply a mix_aoovl file.
MO coefficients
MO coefficients of the bra and ket wavefunctions can usually be read in directly in the form written by the quantum chemistry program.
The supported options for a_mo_read and b_mo_read are 0 for COLUMBUS format, 1 for MOLCAS lumorb format, and 2 for TURBOMOLE format.
Because the number of electrons strongly affects the run time of wfoverlap.x, it is generally beneficial to apply a frozen core approximation, even if the actual wave function calculation did not do so.
Most interfaces which use wfoverlap.x have a keyword numfrozcore in the resource file, which only affects the number of frozen core orbitals for the overlap calculation (If the interface support frozen core for the quantum chemistry itself, there will be a keyword in the template file).
Slater determinants and CI coefficients
Slater determinants and CI coefficients are currently supplied by an ASCII file of the form
3 7 168 dddddee 0.979083342437 0.979083342437 -0.122637656388 ddddabe -0.094807515471 -0.094807515471 -0.663224542162 ddddbae 0.094807515471 0.094807515471 0.663224542162 ...
The first line specifies
- the number of states (columns in the file),
- the number of MOs (length of the determinant strings), and
- the number of determinants in the file (length of the file).
Every subsequent line gives the determinant string and the corresponding CI coefficients for the different states.
The following symbols are used in the determinant string:
- d – doubly occupied
a – singly occupied (α)
b – singly occupied (β)
e – empty
Most relevant for SHARC users, the wfoverlap.x program fully considers all determinants inside these files, without applying any form of truncation. Hence, truncation of long wave functions is done during the creation of the determinant files.
Most interfaces which write these files have a keyword wfthres in their resource file. This threshold is a number between 0.0 and 1.0, and is the minimum wave function norm to which the wave functions should be truncated. During truncation, the interfaces generally retain the largest-amplitude CI coefficients, and remove determinants with small coefficients, i.e., they find the truncated expansion with the fewest determinants which has a norm above the wfthres.
Choosing this threshold properly can very strongly affect the computational time spent in the overlap calculation. Generally, for CASSCF wave functions the threshold can be set to 1 (SHARC_MOLPRO.py, SHARC_MOLCAS.py, and SHARC_BAGEL.py always use all determinants and do not have the wfthres option), for TDA-DFT/ADC(2) it should usually be well above 0.99, for and for MRCI wave functions it might be necessary to go as low as 0.95, depending on the accuracy and performance needed.
For TD-DFT calculations without the Tamm-Damcoff approximation, the response vectors are usually normalized to |X|2−|Y|=1, but only X is used in the overlap calculation; since the norm of X can thus exceed 1, the wfthres should be increased above 1, too.
As a rule of thumb, the threshold should always be chosen such that each state is represented by at least a few 100 determinants in the file, in order to obtain smoothly varying overlaps.
If unsure, the user should perform a test calculation, varying the wfthres until a suitable one is found (i.e., with as many determinants as possible such that the cost of the overlap calculation is bearable).
6.13.5 Output
Usually, the output of wfoverlap.x is automatically extracted by the interfaces, and reported in QM.out in the overlap or 2D-property sections.
Wavefunction overlaps
The output first lists some information about the wavefunction structure and about the computational time taken for the individual steps (cf. Figure 6.3).
A typical result of a wavefunction overlap computation is shown here:
Overlap matrix <PsiA_i|PsiB_j> |PsiB 1> |PsiB 2> <PsiA 1| 0.5162656622 -0.2040109070 <PsiA 2| -0.2167057391 -0.5266552021 Renormalized overlap matrix <PsiA_i|PsiB_j> |PsiB 1> |PsiB 2> <PsiA 1| 0.5162656622 -0.2040109070 <PsiA 2| -0.2167057391 -0.5266552021 Performing Lowdin orthonormalization by SVD... Orthonormalized overlap matrix <PsiA_i|PsiB_j> |PsiB 1> |PsiB 2> <PsiA 1| 0.9273847015 -0.3741090956 <PsiA 2| -0.3741090956 -0.9273847015
Overlap matrix gives the raw overlap values
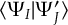 |
(6.7) |
of the wavefunctions supplied.
Renormalized overlap matrix gives the renormalized overlap values
 |
(6.8) |
relevant in the case of wavefunction truncation.
The Orthonormalized overlap matrix is constructed according to a procedure described in more detail in Ref. [74].
Dyson orbitals
The matrix of Dyson norms is printed at the end of the file
ALPHA ionization Dyson norm matrix |<PsiA_i|PsiB_j>|^2 |PsiB 1> |PsiB 2> |PsiB 3> <PsiA 1| 0.8817323437 0.4716319904 0.0680618001 <PsiA 2| 0.0615587916 0.4657174978 0.8772909828 <PsiA 3| 0.0000000000 0.0363130811 0.0000000000 <PsiA 4| 0.9634885049 0.0000000000 0.0017379586 <PsiA 5| 0.0000000000 0.9261839484 0.0000000000
In the case of moprint=1 the orbitals are printed, as well.
The expansion is given with respect to the MOs of the neutral system.
Dyson orbitals in reference |ket> MO basis: <PsiA 1| |PsiB 1> |PsiB 2> |PsiB 3> MO 1 -1.24032037E-03 0.00000000E+00 9.98160731E-04 MO 2 -5.90277699E-02 0.00000000E+00 6.14517859E-02 MO 3 -1.23295110E-09 0.00000000E+00 3.08416849E-10 MO 4 0.00000000E+00 -6.86713110E-01 0.00000000E+00 MO 5 9.31351013E-01 0.00000000E+00 -2.49427166E-01 MO 6 -3.50106110E-02 0.00000000E+00 4.19935829E-02 MO 7 -1.83303166E-10 0.00000000E+00 -3.67409953E-12 MO 8 -1.91183349E-10 0.00000000E+00 9.40768334E-11 ...
Chapter 7
Auxilliary Scripts
In this chapter, all auxiliary scripts and programs are documented. Input generators (like molpro_input.py and molcas_input.py) are documented in the relevant interface sections.
All auxiliary scripts are either interactive-prompting user input from stdin in order to setup a certain task-or non-interactive, meaning they are controlled by command-line arguments and options, in the same way as many standard command-line tools work.
All interactive scripts sequentially ask a number of questions to the user. In many cases, a default value is presented, which is either preset or detected by the scripts based on the availability of certain files. Furthermore, the scripts feature auto-completion of paths and filenames (use TAB), which is active only in questions where auto-completion is relevant. For certain questions where lists of integers needs to be entered, ranges can be indicated with the tilde symbol (), e.g., -8-2 (note that no spaces are allowed between the tilde and the two numbers) to indicate the list -8 -7 -6 -5 -4 -3 -2.
All interactive scripts write a file called KEYSTROKES.<script_name> which contains the user input from the last completed session. These files can be piped to the interactive scripts to perform the same task again, for example:
user@host> cat KEYSTROKES.excite - | $SHARC/excite.py
Note the -, which tells cat to switch to stdin after the file ends, so that the user can proceed if the script asks for more input than contained in the KEYSTROKES file.
All non-interactive scripts can be called with the -h option to obtain a short description, usage information and a list of the command line options.
Non-interactive scripts also write a KEYSTROKES.<script_name> file, which will contain the last command entered to execute the script (including all options and arguments).
All scripts can be safely killed during a run by using Ctrl-C. In the case of interactive scripts, a KEYSTROKES.tmp file remains, containing the user input made so far. Note that the KEYSTROKES.tmp file cannot be directly piped to the scripts, because KEYSTROKES.tmp will be overwritten when the script starts.
7.1 Wigner Distribution Sampling: wigner.py
The first step in preparing the dynamics calculation is to obtain a set of physically reasonable initial conditions. Each initial condition is a set of initial atomic coordinates, initial atomic velocities and initial electronic state. The initial geometry and velocities can be obtained in different ways. With SHARC, often sampling of a quantum-harmonic Wigner distribution is performed.
The sampling is carried out with the non-interactive Python script wigner.py. The theoretical background is summarized in section 8.24.
7.1.1 Usage
The general usage is
user@host> $SHARC/wigner.py [options] filename.molden
wigner.py takes exactly one command-line argument (the input file with the frequencies and normal modes), plus some options. Usually, the -n option is necessary, since the default is to only create 3 initial conditions.
The argument is the filename of the file containing the information about the vibrational frequencies and normal modes. The file is by default assumed to be in the MOLDEN format. For usage with wigner.py, only the following blocks have to be present:
|
The script accepts a number of command-line options, specified in table 7.1.
| Option | Description | Default |
| -h | Display help message and quit | – |
| -n INTEGER | Number of initial conditions to generate | 3 |
| -m | Modify atom masses (starts interactive dialog) | Most common isotopes |
| -s FLOAT | Scaling factor for the frequencies | 1.0 |
| -t FLOAT | Use Boltzmann-weighted distribution at the given temperature | 0.0 K |
| -T | Discard very high vibrational states at high temperatures | Don’t discard, but warn |
| -L FLOAT | Discard frequencies below the given one (in cm−1) | 10.0 |
| -o FILENAME | Output filename | initconds |
| -x | Creates an xyz file with the sampled geometries | initconds.xyz |
| -l | Instead of generating initconds, create input for SHARC_LVC.py | Create initconds |
| -r INTEGER | Seed for random number generator | 16661 |
| -f F | Type of normal modes read (0=detect automatically, 1-4=see below) | 0 |
| -keep_trans_rot | Do not remove translations and rotations from velocity vector | |
| -use_eq_geom | Sample only velocities, but keep equilibrium geometry | Sample normally |
| -use_zero_veloc | Sample only geometries, but set velocities to zero | Sample normally |
7.1.2 Normal mode types
The normal mode vectors contained in a MOLDEN file can follow different conventions, e.g., unscaled Cartesian displacements or different kinds of mass-weighted displacements.
By default, wigner.py attempts to identify which convention is followed by the file (by performing different renormalizations and checking if the so-obtained matrix is orthogonal).
In order to use this automatic detection, use -f 0, which is the default.
Otherwise, there are four possible options: -f 1 to assume normal modes in the GAUSSIAN convention (used by GAUSSIAN, TURBOMOLE, Q-CHEM, ADF, and ORCA); -f 2 to assume Cartesian normal modes (used by MOLCAS and MOLPRO); -f 3 to assume the COLUMBUS convention; or -f 4 for mass-weighted, orthogonal normal modes.
7.1.3 Non-default masses
When the -m option is used, the script will ask the user to interactively modify the atom masses. For each atom (referred to by the atom index as in the MOLDEN file), a mass can be given (relative atomic weights). Note that the frequency calculation which produces the MOLDEN should be done with the same atomic masses.
7.1.4 Sampling at finite temperatures
When the -t option is used, the script assumes a finite, non-zero temperature.
The sampling will then consist of two steps, where first randomly a vibrational state is picked from the Boltzmann distribution, and then the Wigner distribution of that state is employed.
For more details, see Section 8.24.
At high temperatures and for low-frequency modes it is possible that very large vibrational quantum numbers will be selected.
Because of the occurrence of factorials in the Laguerre polynomials in the excited Wigner distributions, this leads to variable overflow for νvib > 150. Hence, the highest vibrational quantum number considered is 150, and higher ones are set to 150.
Since this can lead to an overrepresentation of νvib=150, with the -T option one can instead discard all samplings where νvib > 150.
No matter whether -T is used or not, keep in mind that usually such high vibrational states might invalidate the assumption of an harmonic oscillator, and other sampling methods (e.g., molecular dynamics) should be considered.
7.1.5 Output
The script wigner.py generates a single output file, by default called initconds. All information about the initial conditions is stored in this file. Later steps in the preparation of the initial conditions add information about the excited states to this file. The file is formatted in a human-readable form.
The initconds file format is specified in section 7.6.5.
When the -x option is given, additionally the script produces a file called initconds.xyz, which contains the sampled geometries in standard xyz format. This can be useful to inspect the distribution of geometry parameters (e.g., bond lengths) or to perform single point calculations at the sampled geometries.
When the -l option is given, the script only produces a file called V0.txt, which is a necessary input file for the LVC interface (see section 6.9). If this option is activated, no initconds or initconds.xyz files are produced.
7.2 Vibrational State Selected Sampling: state_selected.py
In addition to wigner.py one can use state_selected.py to perform vibrational state selected initial conditions. In that situation, one can specify the vibrational level for each normal mode.
7.2.1 Usage
The general usage is
user@host> $SHARC/state_selected.py [options] filename.molden
state_selected.py takes exactly one command-line argument (the input file with the frequencies and normal modes), plus some options. Usually, the -vibselec, -vibdist, -vibstate or -vibene, and -n options are necessary, the default is to only create 3 initial conditions.
Smae as wigner.py, the argument is the filename of the file containing the information about the vibrational frequencies and normal modes. The file is by default assumed to be in the MOLDEN format. For usage with wigner.py, only the following blocks have to be present:
|
The script accepts a number of command-line options, specified in table 7.2.
The descriptions of major options including -vibselect, -vibdist, -vibstate, -vibene, -method, -template will be described in next section.
| Option | Description | Default |
| -vibselect | Method to select the vibrational mode energy. | 3 |
| -vibdist | Method to determin phase space distribution. | 0 |
| -vibstate | List of vibrational state for each mode. | 0 |
| -vibene | List of vibrational energy for each model | 0.0 |
| -method | Method to determine the approximation for energy | 0 |
| -template | name of the template file to interface with electronic structure calculations. This is only needed when using -method 1. | |
| -h | Display help message and quit | – |
| -n INTEGER | Number of initial conditions to generate | 3 |
| -m | Modify atom masses (starts interactive dialog) | Most common isotopes |
| -s FLOAT | Scaling factor for the frequencies | 1.0 |
| -t FLOAT | Use Boltzmann-weighted distribution at the given temperature | 0.0 K |
| -T | Discard very high vibrational states at high temperatures | Don’t discard, but warn |
| -L FLOAT | Discard frequencies below the given one (in cm−1) | 10.0 |
| -o FILENAME | Output filename | initconds |
| -x | Creates an xyz file with the sampled geometries | initconds.xyz |
| -r INTEGER | Seed for random number generator | 16661 |
| -f F | Type of normal modes read (0=detect automatically, 1-4=see below) | 0 |
| -keep_trans_rot | Do not remove translations and rotations from velocity vector | |
| -use_eq_geom | Sample only velocities, but keep equilibrium geometry | Sample normally |
| -use_zero_veloc | Sample only geometries, but set velocities to zero | Sample normally |
7.2.2 Major options
The sate_selected.py script involves five major options to perform vibrational state selection.
-vibselect determins the method to select the vibrational mode energy.
-vibselect 1, the user will provide a list of vibrational quantum numbers, and will require keyword -vibstate.
-vibselect 2, the program will assign vibrational quantum numbers for each mode. This assignment is random, and selected out of a Boltzmann distribution at a user-speficied temperature that is speficied by the option -t.
-vibselect 3, the program generates an initial velocity from a Maxwell thermal distribution at a given temperature by option -t. This is an option for canonical ensemble, not an option for state selected ensemble. This option is not available at the moment.
-vibselect 4, the amount of energy in each mode is the same, and is set by option -vibene E, where E is the energy of each mode.
-vibselect 5, the amount of energy in each mode is different, and is set option -vibene E1, E2, E3, ..., where E1, E2, E3, ... is a list of energy for each mode.
-vibselect 6, default, similar as -vibselect 4, but the energy of each mode is computed as minimum of zero point energy and E.
-vibselect 7, similar as -vibselect 5, but the energy of each mode is computed as minimum of zero point energy and EI, where I is the index of mode.
-vibdist determins the type of phase space distribution.
-vibdist 0, default, uses quasiclassical or classical distribution. It is a uniform distribution. It is quasiclassical if vibselect=1 or vibselect=2, it is classical if vibselect ≥ 4.
-vibdist 1, ground state harmonic oscillator distribution.
-vibdist 2, Wigner distribution.
-vibstate is a list of vibrational quantum number for all mode or each mode. For example, -vibstate 0 specifies all vibrational mode with 0 quantum number, i.e. all mode have zero point energy; -vibstate 0,1,2,... specifies the quantum number for each mode, in this example, the first three modes have vibrational quantum numbers as 0, 1, and 2 respectively.
-vibene is a list of vibrational energy for all mode or each mode. For example, -vibene 0.2 specifies all vibrational mode with 0.2 eV of vibrational energy; -vibene 0.1,0.2,0.1,... specifies the vibrational energy for each mode, in this example, the first three modes have vibrational energies of 0.1 eV, 0.2 eV, and 0.1 eV respectively.
-method determines the level of energies are computed when the geometries is away from the equilibrium structure. Notice that we only provide the vibrational frequency at equilibrium structure. When one samples initial geometry, the energy of that geometry can either be computed with harmonic oscillator approximation by knowing the vibrational frequencies, or computed directly from electronic structure softwares. -method 0 uses harmonic oscillator approximation, and -method 1 uses direct computation. Notice that if one uses direct computation, one is required to provide an additional option -tempalate, which specifies a script that interfacing with electronic structure calculations.
-template keyword follows by a file name that is a script serves as interface between the state_selected.py and electronic structure software. When using ab initio potential, i.e. when set -method 1, the state_selected.py will write a file called tmp_state_selected.xyz everytime it samples a new geometry, and execute the script, then read the energy from an output file called energy_state_selected. Therefore, the function of this userdefined script is to read tmp_state_selected.xyz, and write energy into file energy_state_selected.
The following bash script shows an example of such a script. In which it reads the tmp_state_selected.xyz, write a Gaussian density functional calculation with MN15 functional and def2-TZVP basis set, and store the density functional energy into file energy_state_selected
#!/bin/bash
#write a Gaussian input
echo "%Chk=e.chk" > e1.tmp
echo "%Mem=11800mb" >> e1.tmp
echo "#P def2TZVP SCF=(Tight,novracc,maxcycle=500) Integral(Grid=UltraFine) MN15" >> e1.tmp
echo " " >> e1.tmp
echo "my molecule" >> e1.tmp
echo "0 1" >> t1.tmp
echo " " > e2.tmp
echo " " >> e2.tmp
cat e1.tmp tmp_state_selected.xyz e2.tmp > e.com
#run a Gaussian calculation
/software/g09/g09 < e.com > e.out
#save the energy into energy_state_selected
grep 'SCF Done' e.out|awk '{print $5}' > energy_state_selected
7.2.3 Normal mode types
The normal mode vectors contained in a MOLDEN file can follow different conventions, e.g., unscaled Cartesian displacements or different kinds of mass-weighted displacements.
By default, state_selected.py attempts to identify which convention is followed by the file (by performing different renormalizations and checking if the so-obtained matrix is orthogonal).
In order to use this automatic detection, use -f 0, which is the default.
Otherwise, there are four possible options: -f 1 to assume normal modes in the GAUSSIAN convention (used by GAUSSIAN, TURBOMOLE, Q-CHEM, ADF, and ORCA); -f 2 to assume Cartesian normal modes (used by MOLCAS and MOLPRO); -f 3 to assume the COLUMBUS convention; or -f 4 for mass-weighted, orthogonal normal modes.
7.2.4 Non-default masses
When the -m option is used, the script will ask the user to interactively modify the atom masses. For each atom (referred to by the atom index as in the MOLDEN file), a mass can be given (relative atomic weights). Note that the frequency calculation which produces the MOLDEN should be done with the same atomic masses.
7.2.5 Output
The script state_selected.py generates a single output file, by default called initconds. All information about the initial conditions is stored in this file. Later steps in the preparation of the initial conditions add information about the excited states to this file. The file is formatted in a human-readable form.
The initconds file format is specified in section 7.6.5.
When the -x option is given, additionally the script produces a file called initconds.xyz, which contains the sampled geometries in standard xyz format. This can be useful to inspect the distribution of geometry parameters (e.g., bond lengths) or to perform single point calculations at the sampled geometries.
7.3 AMBER Trajectory Sampling: amber_to_initconds.py
The first step in preparing the dynamics calculation is to obtain a set of physically reasonable initial conditions. Each initial condition is a set of initial atomic coordinates, initial atomic velocities and initial electronic state. The initial geometry and velocities can be obtained in different ways.
Besides sampling from a quantum mechanical Wigner distribution (with wigner.py), it is a widespread approach to sample geometries and velocities from a ground state molecular dynamics simulation.
Using amber_to_initconds.py, one can convert the results of an AMBER simulation to a SHARC initconds file.
7.3.1 Usage
In order to use amber_to_initconds.py, it is necessary to first carry out an AMBER simulation.
You need to add the following options to the AMBER MD input file: (i) ntxo=1 to tell AMBER to write ASCII restart files, (ii) ntwr=-5000 to create a restart file every 5000 steps (other values are possible, but use the minus to not overwrite the restart files).
This will create a set of AMBER restart files called, e.g., md.rst_5000, md.rst_10000, …
Note that it is also necessary to reimage the AMBER restart files, because SHARC does not work with periodic boundary conditions, but the AMBER trajectories might use them.
The reimaging can be performed with AMBER‘s tool cpptraj, using the following input:
parm <filename>.prmtop trajin <filename>.rst7 autoimage trajout <filename2>.rst7 run
This command has to be repeated for each restart file which needs to be reimaged.
Note that amber_to_initconds.py only works with the rst7 ASCII file format, not with the rst format (even if it is ASCII-formatted).
If you saved the restart files in AMBER‘s newer NetCDF format, cpptraj can also be used to convert them to ASCII rst7 restart files.
If you did not save restart files, cpptraj can even be used to generate restart files from the trajectory file (.mdcrd and .mdvel), but for this way it is necessary to save the velocities (.mdvel file).
With the restart files prepared, call amber_to_initconds.py like this:
user@host> $SHARC/amber_to_initconds.py [options] md.prmtop md.rst_0 md.rst_5000 md.rst_10000 ...
The possible options are shown in Table 7.3.
| Option | Description | Default |
| -h | Display help message and quit | – |
| -t FLOAT | Time step (in femtoseconds) used in the AMBER simulation | – |
| -o FILENAME | Output filename | initconds |
| -x | Creates an xyz file with the sampled geometries | initconds.xyz |
| -m | Modify atom masses (starts interactive dialog) | As in prmtop file |
| -keep_trans_rot | Do not remove translations and rotations from velocity vector | |
| -use_zero_veloc | Sample only geometries, but set velocities to zero | Sample normally |
7.3.2 Time Step
Note that the option -t (giving the time step used in AMBER in femtoseconds) is mandatory; if not given, an error message is produced.
This is because AMBER uses a Leapfrog algorithm and thus stores in the restart file R(t) and v(t−∆t/2), whereas SHARC uses the velocity-Verlet algorithm and requires geometry and velocity at the same time, e.g., R(t−∆t/2) and v(t−∆t/2).
To compensate this, amber_to_initconds.py computes R(t−∆t/2) from R(t)−v(t−∆t/2)∆t/2.
Hence, ∆t of the AMBER trajectory needs to be known.
7.3.3 Atom Types and Masses
By default, atom types and masses are read from the prmtop file (from flags ATOMIC_NUMBER and MASS).
If the atomic number is not sensible (e.g., -1 for a transition metal) then amber_to_initconds.py prompts the user to define the element.
The masses in the prmtop file can be overridden if the -m option is given; then the user can adjust the mass of each atom individually.
7.3.4 Output
amber_to_initconds.py produces the same output as wigner.py (section 7.1).
By default, a file called initconds is generated for the converted initial conditions.
It is important to note that the first restart file given (the second command line argument) is treated as the “equilibrium” geometry for the purpose of generating the initconds file.
The second given restart file is then converted to the initial condition with index 1, and so on.
Note that it is possible to give the same restart file multiple times as an argument (so that the same geometry can be used as “equilibrium” geometry and as proper initial condition.
7.4 SHARC Trajectory Sampling: sharctraj_to_initconds.py
The first step in preparing the dynamics calculation is to obtain a set of physically reasonable initial conditions. Each initial condition is a set of initial atomic coordinates, initial atomic velocities and initial electronic state. The initial geometry and velocities can be obtained in different ways.
Besides sampling from a quantum mechanical Wigner distribution, it is often appropriate to sample geometries and velocities from a ground state molecular dynamics simulation.
Using sharctraj_to_initconds.py, one can convert the results of a SHARC simulation to a new SHARC initconds file.
7.4.1 Usage
In order to use sharctraj_to_initconds.py, it is necessary to first run a number of SHARC trajectories (the initial conditions for those need to be obtained with wigner.py or amber_to_initconds.py).
The trajectories can be run with any number of states and in any state, and with any desirable options; only geometries and velocities are converted to the new initconds file.
With the trajectories prepared, call sharctraj_to_initconds.py like this:
user@host> $SHARC/sharctraj_to_initconds.py [options] Singlet_0 ...
Alternatively, with the -give_TRAJ_paths option, one can also do:
user@host> $SHARC/sharctraj_to_initconds.py --give_TRAJ_paths [options] TRAJ_00001 TRAJ_00002 ...
The possible options are shown in Table 7.4.
| Option | Description | Default |
| -h | Display help message and quit | – |
| -r INTEGER | Seed for the random number generator | 16661 |
| -S INTEGER INTEGER | Range of time steps from which a step is randomly chosen | last step |
| -o FILENAME | Output filename | initconds |
| -x | Creates an xyz file with the sampled geometries | initconds.xyz |
| -keep_trans_rot | Do not remove translations and rotations from velocity | |
| -use_zero_veloc | Sample only geometries, but set velocities to zero | Sample normally |
| -debug | Show timings | |
| -give_TRAJ_paths | Allows specifying individual trajectories | Specify parent directories |
7.4.2 Random Picking of Time Step
For each directory specified as command line argument, sharctraj_to_initconds.py picks exactly one time step and extracts geometries and velocities of that time step.
Note that a directory can be given several times as argument, so that multiple time steps can be selected.
The time steps are generally picked randomly (uniform probabilities) from an interval specified with the -S option.
This option takes two integers, e.g., -S 50 -50, which can be positive or negative.
The meaning of positive/negative/zero is the same as in PYTHON: positive numbers simply denote a time step (start counting with zero for the step zero of the trajectory); for negative numbers, start counting at the end, i.e., -1 is the last time step of the trajectory.
In this way, it is possible to select the snapshot from the last n steps of all trajectories, even if they have different length.
The example above, -S 50 -50, means picking a time step between the 50th and the 50th-last step. Note that if a trajectory is shorter than 100 steps, in this example it is skipped because there are no steps between the 50th and the 50th-last step.
7.4.3 Output
sharctraj_to_initconds.py produces the same output as wigner.py (section 7.1).
By default, a file called initconds is generated for the converted initial conditions.
It is important to note that the first directory given (the first command line argument) is treated as the “equilibrium” geometry for the purpose of generating the initconds file.
The second given directory is then converted to the initial condition with index 1, and so on.
Note that it is possible to give the same directory multiple times as an argument (so that the same geometry can be used as “equilibrium” geometry and as proper initial condition.
7.5 Setup of Initial Calculations: setup_init.py
The interactive script setup_init.py creates input for single point calculations at the initial geometries given in an initconds file. These calculations might be necessary for some schemes to select the initial electronic state of the trajectory, e.g., based on the excitation energies and oscillator strength of the transitions from ground state to the excited state, or based on overlaps with a reference wave function.
There are other choices of the initial state possible, which do not require single point calculations at all initial geometries. See the description of excite.py (section 7.6). In this case, setup_init.py can be used to set up only the calculation at the equilibrium geometry (see below at “Range of Initial Conditions”).
7.5.1 Usage
The script is interactive, and can be started by simply typing
user@host> $SHARC/setup_init.py
Please be aware that the script will setup the calculations in the directory where it was started, so the user should cd to the desired directory before executing the script.
Please note that the script does not expand or shell variables, except where noted otherwise.
7.5.2 Input
The script will prompt the user for the input. In the following, all input parameters are documented:
Initial Conditions File
Enter the filename of the initial conditions file, which was generated beforehand with wigner.py. If the script finds a file called initconds, the user is asked whether to use this file, otherwise the user has to enter an appropriate filename. The script detects the number of initial conditions and number of atoms automatically from the initial conditions file.
Range of Initial Conditions
The initial conditions in initconds are indexed, starting with the index 1. In order to prepare ab initio calculations for a subset of all initial conditions, enter a range of indices, e.g. a and b. This will prepare all initial conditions with indices in the interval [a,b]. In any case, the script will additionally prepare a calculation for the equilibrium geometry (except if a finished calculation for the equilibrium geometry was found).
If the interval [0,0] is given, the script will only setup the calculation at the equilibrium geometry.
Number of states
Here the user can specify the number of excited states to be calculated. Note that the ground state has to be counted as well, e.g., if 4 singlet states are specified, the calculation will involve the S0, S1, S2 and S3. Also states of higher multiplicity can be given, e.g. triplet or quintet states.
For even-electron molecules, including odd-electron states (e.g. doublets) is only useful if transition properties for ionization can be computed (e.g. Dyson norms with some of the interfaces). These transition properties can be used to calculate ionization spectra or to obtain initial conditions for dynamics after ionization.
Interface
In this point, choose any of the displayed interfaces to carry out the ab initio calculations. Enter the corresponding number.
Spin-orbit calculation
Usually, it is sufficient to calculate the spin-free excitation energies and oscillator strengths in order to decide for the initial state. However, using this option, the effects of spin-orbit coupling on the excitation energies and oscillator strengths can be included. Note that the script will never calculate spin-orbit couplings if only singlet states are included in the calculation, or if the chosen interface does not support calculation of spin-orbit couplings.
Reference overlaps
The calculations can be setup in such a way that the wave function overlaps between states at the equilibrium geometry and the displaced geometries is computed.
This allows correlating the states at the displaced geometries with the reference states, such that one can know the state characters of all states without inspection.
This is useful for a crude “diabatization” of the states, e.g., if one wants to start all trajectories in the nπ* state of the molecule although this state can be S1, S2, or S3 (use excite.py to setup initial conditions in such a way, see section 7.6).
When activating this option, keep in mind that the calculation in ICOND_00000 must be successfully finished before any of the other ICOND_XXXXX calculations can be started.
TheoDORE analysis
If the chosen interface supports wave function analysis with TheoDORE, then this option can be activated here.
setup_init.py will then include the relevant keywords in the computations, and the results of the TheoDORE analysis will be written to the QM.out files.
The remaining settings for TheoDORE (fragment and descriptor input) will be asked later in setup_init.py.
7.5.3 Interface-specific input
The following input in setup_init.py depends on the chosen interface.
However, some input is similar between several interfaces and is discussed (out of input order) in section 7.5.3.
Note that most of the questions asked in the input dialogue have some counterpart in the resource file of the chosen interface, so you might find additional information in chapter 6.
Input which is similar between interfaces
Path to quantum chemistry programs and licenses
Here the user is prompted to provide the path to the relevant executables or installation directories.
Note that the setup script will not expand the user ( ) and shell variables (since the calculations might be running on a different machine than the one used for setup, so the meaning of shell variables could be different). and shell variables will only be expanded by the interfaces during the actual calculation.
For some interfaces, also the path to a license file might need to be specified.
Scratch directory
The script takes the string without any checking. Each individual initial condition uses a subdirectory of the given path, so that there are no clashes between the initial conditions. and shell variables will only be expanded by the interface during the actual calculation.
Note that you can use, e.g., ./temp/ as scratch directory, which is a subdirectory of the working directory of the interface. Using ./ as scratch directory is not recommended, since the interface will delete the scratch directory.
Template file
For almost all interfaces, setup_init.py will ask for a template file containing the quantum chemistry specifics of the calculations. The format of the template file depends on the interface; formats are described in the interface chapter 6.
For most interfaces, setup_init.py will perform some basic checks, but ultimately the template file will be checked by the interface once the calculation is submitted.
Initial orbital guess
For some interfaces, setup_init.py will ask for files containing initial orbital guesses. providing initial is especially important for multi-reference calculations, because otherwise it is very likely that the calculations converge to an undesirable active space.
Resource usage
For most interfaces, setup_init.py will ask for the amount of memory and the number of CPU cores to use. For some interfaces, additionally a delay between the start of parallel calculation can be provided (this might be helpful if many calculations starting at the same time is problematic for I/O).
For the MOLCAS, ADF, Gaussian, and ORCA interfaces, furthermore the schedule_scaling is queried for (see section 8.3 for details).
Wavefunction overlap program
The scripts asks for the path to the wavefunction overlap program. In a complete SHARC installation, the overlap program should be located at $/SHARC/wfoverlap.x.
Depending on the interface, the script might also ask for the threshold to truncate the wave function files, or for the memory for wfoverlap.x (if the memory of the quantum chemistry program cannot be set).
For some interfaces, it is also possible to control the number of frozen core orbitals for the overlap calculation (and the number of inactive orbitals for Dyson orbital calculations).
THEODORE setup
If THEODORE is enabled, setup_init.py will query for the path to the THEODORE installation directory. Furthermore, the user needs to enter a list of the descriptors to be calculated by THEODORE, as well as the atom indices for each fragment for the charge transfer number computation.
QM/MM setup
For some interfaces, setup_init.py will ask for QM/MM-related files if the template file specifies a QM/MM calculation.
Currently, the QM/MM setup consists simply of providing the relevant interface-specific files to setup_init.py, which it simply copies accordingly.
Input for MOLPRO
Path to MOLPRO
Here the user is prompted to provide the path to the MOLPRO executable.
For more details, see section 7.5.3.
Scratch directory
See section 7.5.3.
Template file
Enter the filename for the MOLPRO template input. This file should contain at least the basis set, active orbitals and electrons, number of electrons and number of states for state-averaging. For details, see the section about the SHARC– MOLPRO interface (6.3). The setup script will check whether the template file contains the necessary entries.
Initial wave function file
You can provide an initial wave function (with an appropriate MO guess) to MOLPRO. This usually provides a drastic speedup for the CASSCF calculations and helps in ensuring that all calculations are based on the same active space. In simple cases it might be acceptable to not provide an initial wave function.
Resource usage
The script asks for the memory and number of CPU cores to be used. Note that both settings apply to MOLPRO and to wfoverlap.x, if the latter is required (but note that the two programs are never run simultaneously).
If more than one CPU core is used, the interface will parallelize different MOLPRO runs (but will not run MOLPRO in parallel mode); wfoverlap.x will be run in SMP-parallel mode.
Wavefunction overlap program
See section 7.5.3. Note that for the MOLPRO interface, no truncation threshold can be given, since wfoverlap.x is very efficient for CASSCF wavefunctions.
Input for MOLCAS
Path to MOLCAS
Here the user is prompted to provide the path to the MOLCAS directory.
For more details, see section 7.5.3.
Scratch directory
See section 7.5.3.
Template file
Enter the filename for the MOLCAS template input. This file should contain at least the basis set, active orbitals and electrons, number of inactive orbitals, and number of states for state-averaging. For details, see the section about the SHARC– MOLCAS interface (6.4). The setup script will check whether the template file contains the necessary entries.
QM/MM
If the keyword qmmm is contained in the template file, the user will be queried for the path to TINKER‘s bin/ directory. Note that only TINKER installations with the necessary modifications for MOLCAS can be used.
The script will also ask for the key file (containing the path to the force field file and the QM/MM partition) and the connection table file. See section 6.4 for details.
Initial wave function file
You can provide initial MO coefficients to MOLCAS. This usually provides a drastic speedup for the CASSCF calculations and helps in ensuring that all calculations are based on the same active space. In simple cases it might be acceptable to not provide an initial wave function. For MOLCAS, you have to specify one file for each multiplicity (but you can use the same file as guess for several multiplicities).
Initial orbital files can either be in JobIph or RasOrb format.
Resource usage
The script asks for the memory and number of CPU cores to be used. Note that both settings apply to MOLCAS and to wfoverlap.x, if the latter is required (but note that the two programs are never run simultaneously).
If more than one CPU core is used, the interface will parallelize different MOLCAS runs (but will not run MOLCAS in parallel mode); wfoverlap.x will be run in SMP-parallel mode.
Wavefunction overlap program
See section 7.5.3. The wfoverlap.x program is only required if Dyson norms need to be calculated. Note that for the MOLCAS interface, no truncation threshold can be given, since wfoverlap.x is very efficient for CASSCF wavefunctions.
Input for COLUMBUS
Path to COLUMBUS
Here the user is prompted to provide the path to the COLUMBUS directory.
For more details, see section 7.5.3.
Scratch directory
See section 7.5.3.
Template directory
Enter the path to a directory containing subdirectories with COLUMBUS input files necessary for the calculations. The setup script will expand and shell variables and will pass the absolute path to the calculations.
The script will auto-detect (based on the cidrtin files) which subdirectory contains the input for each multiplicity. The user has to check in the following dialog whether the association of multiplicities with job directories is correct. Additionally, the association of MO coefficient files to the jobs has to be checked. See the section on the SHARC– COLUMBUS interface (6.5) for further details.
Note that the setup script does not check any content of the input files beyond the multiplicity. Note that transmomin and control.run do not need to be present (and that their content has no effect on the calculation), since these files are written on-the-fly by the interface.
The template directory can either be linked or copied to the initial condition calculations.
Initial orbital coefficient file
You can provide initial MO coefficients for the COLUMBUS calculation. This usually provides a drastic speedup for the CASSCF calculations and helps to ensure that all calculations are based on the same active space. In simple cases it might be acceptable to not provide an initial wave function.
Memory
For COLUMBUS, the available memory must be given here. The COLUMBUS interface does not allow for parallelization currently.
Wavefunction overlap program
See section 7.5.3. For CASSCF calculations with COLUMBUS, use a truncation threshold of 1.0, for MRCIS/MRCISD calculations, 0.97-0.99 should provide sufficient performance and accuracy.
Input for analytical potentials
Template file
Enter the filename for the template input specifying the analytical potentials. For details, see the section about the SHARC-Analytical interface (6.6). The setup script will check whether the template file is valid.
Input for ADF
Path to ADF
Here the user is first asked if setup should be made from an adfrc.sh file. If yes, only the path to this file is needed.
Otherwise, the path to the ADF installation directory and the path to the license file need to be provided.
For more details, see section 7.5.3.
Scratch directory
See section 7.5.3.
Template file
Enter the filename for the ADF template input. This file should contain at least the basis set, functional, and charge keywords. For details, see the section about the SHARC– ADF interface (6.7). The setup script will check whether the template file contains the necessary entries.
QM/MM
The script will ask for the two QM/MM-specific input files for the interface, which are called ADF.qmmm.ff and ADF.qmmm.table.
See section 6.7 for details on these files.
Initial orbital coefficient file
You can provide initial MO coefficients for the ADF calculation. This can provide a small speedup for the calculations and helps to ensure that all calculations are based on the same orbitals.
In many cases, no initial orbitals are required.
Resource usage
For ADF, the amount of memory to be used cannot be controlled. However, the number of CPU cores needs to be given. If more than one core is used, also the parallel scaling needs to be specified (see section 8.3).
Wavefunction overlap program
See section 7.5.3. setup_init.py will ask for the memory usage of wfoverlap.x. The truncation threshold for TD-DFT can usually be chosen as 0.99-1.00 (depending on the system and functional, but it is recommended that it is high enough that each state is described by at least 100 determinants in the generated files). See section 6.7 for details.
THEODORE setup
See section 7.5.3.
Input for RICC2
Path to TURBOMOLE
The path to the TURBOMOLE installation directory needs to be provided.
If spin-orbit couplings are requested, also the path to the ORCA installation directory is needed.
For more details, see section 7.5.3.
Scratch directory
See section 7.5.3.
Template file
Enter the filename for the RICC2 template input. This file should contain at least the basis set and charge keywords. For details, see the section about the SHARC– RICC2 interface (6.8). The setup script will check whether the template file contains the necessary entries.
Initial orbital coefficient file
You can provide initial MO coefficients for the TURBOMOLE calculation. This can provide a small speedup for the calculations and helps to ensure that all calculations are based on the same orbitals.
In many cases, no initial orbitals are required.
Resource usage
The amount of memory and the number of CPU cores are required in this section.
Note that the SHARC– RICC2 interface always runs only one TURBOMOLE instance at the same time (if the number of CPU cores is larger than one, it will use the SMP/OMP binaries of TURBOMOLE).
Wavefunction overlap program
See section 7.5.3. setup_init.py will ask for the memory usage of wfoverlap.x. The truncation threshold can usually be chosen as 0.99-1.00 (depending on the system, but it is recommended that it is high enough that each state is described by at least 100 determinants in the generated files). See section 6.8 for details.
THEODORE setup
See section 7.5.3.
QM/MM
The script will ask for the two QM/MM-specific input files for the interface, which are called RICC2.qmmm.ff and RICC2.qmmm.table.
See section 6.8 for details on these files.
Input for LVC interface
Template file
Enter the filename for the template input specifying the LVC parameters. For details, see the section about the SHARC-LVC interface (6.9). The setup script will not check whether the template file is valid.
Input for GAUSSIAN interface
Path to GAUSSIAN
The path to the GAUSSIAN installation directory needs to be provided.
Note that this needs to be the path to the directory containing the GAUSSIAN executables, e.g., g09/g16, l9999.exe, etc.
The interface will automatically detect which GAUSSIAN version is used.
For more details, see section 7.5.3.
Scratch directory
See section 7.5.3.
Template file
Enter the filename for the GAUSSIAN template input. This file should contain at least the basis set, functional, and charge keywords. For details, see the section about the SHARC– GAUSSIAN interface (6.10). The setup script will check whether the template file contains the necessary entries.
Initial orbital coefficient file
You can provide initial MO coefficients for the GAUSSIAN calculation. This can provide a small speedup for the calculations and helps to ensure that all calculations are based on the same orbitals.
In many cases, no initial orbitals are required.
Resource usage
The amount of memory and the number of CPU cores are required in this section. If more than one core is used, also the parallel scaling needs to be specified (see section 8.3).
Wavefunction overlap program
See section 7.5.3. setup_init.py will ask for the memory usage of wfoverlap.x. The truncation threshold for TD-DFT can usually be chosen as 0.99-1.00 (depending on the system and functional, but it is recommended that it is high enough that each state is described by at least 100 determinants in the generated files). See section 6.10 for details.
THEODORE setup
See section 7.5.3.
Input for ORCA interface
Path to ORCA
The path to the ORCA installation directory needs to be provided.
Note that this needs to be the path to the directory containing the ORCA executables, e.g.,orca or orca_fragovl.
For more details, see section 7.5.3.
Scratch directory
See section 7.5.3.
Template file
Enter the filename for the ORCA template input. This file should contain at least the basis set, functional, and charge keywords. For details, see the section about the SHARC– ORCA interface (6.11). The setup script will check whether the template file contains the necessary entries.
Initial orbital coefficient file
You can provide initial MO coefficients for the ORCA calculation. This can provide a small speedup for the calculations and helps to ensure that all calculations are based on the same orbitals.
In many cases, no initial orbitals are required.
Resource usage
The amount of memory and the number of CPU cores are required in this section. If more than one core is used, also the parallel scaling needs to be specified (see section 8.3).
Wavefunction overlap program
See section 7.5.3. setup_init.py will ask for the memory usage of wfoverlap.x. The truncation threshold for TD-DFT can usually be chosen as 0.99-1.00 (depending on the system and functional, but it is recommended that it is high enough that each state is described by at least 100 determinants in the generated files). See section 6.11 for details.
THEODORE setup
See section 7.5.3.
QM/MM
The script will ask for the two QM/MM-specific input files for the interface, which are called ORCA.qmmm.ff and ORCA.qmmm.table.
See section 6.11 for details on these files.
Input for BAGEL interface
Path to BAGEL
The path to the BAGEL installation directory needs to be provided.
Note that this needs to be the path to the main directory of BAGEL, with subdirectories like bin/ or lib/.
For more details, see section 7.5.3.
Scratch directory
See section 7.5.3.
Template file
Enter the filename for the BAGEL template input. This file should contain at least the basis set, active space, and charge keywords. For details, see the section about the SHARC– BAGEL interface (6.12). The setup script will check whether the template file contains the necessary entries.
Initial orbital coefficient file
You can provide initial MO coefficients for the BAGEL calculation. This usually provides a drastic speedup for the CASSCF calculations and helps to ensure that all calculations are based on the same active space. In simple cases it might be acceptable to not provide an initial wave function.
Resource usage
The amount of memory and the number of CPU cores are required in this section. If more than one core is used, also the parallel mode needs to be specified (MPI or OpenMP).
Wavefunction overlap program
See section 7.5.3. setup_init.py will ask for the memory usage of wfoverlap.x. The truncation threshold for TD-DFT can usually be chosen as 0.99-1.00 (depending on the system and functional, but it is recommended that it is high enough that each state is described by at least 100 determinants in the generated files). See section 6.12 for details.
7.5.4 Input for Run Scripts
Run script mode
The script setup_init.py generates a run script (Bash) for each initial condition calculation. Due to the large variety of cluster architectures, these run scripts might not work in every case. It is the user’s responsibility to adapt the generated run scripts to his needs.
setup_init.py can generate run scripts for two different schemes how to execute the calculations. With the first scheme, the ab initio calculations are performed in the directory where they were setup (subdirectories of the directory where setup_init.py was started). Note that the interfaces will still use their scratch directories to perform the actual quantum chemistry calculations. Currently, this is the default option.
With the second option, the run scripts will transfer the input files for each ab initio calculation to a temporary directory, where the interface is started. After the interface finishes all calculations, the results files are transferred back to the primary directory and the temporary directory is deleted. Note that setup_init.py in any case creates the directory structure in the directory where it was started. The name of the temporary directory can contain shell variables, which will be expanded when the script is running (on the compute host).
Submission script
The setup script can also create a Bash script for the submission of all ab initio calculations to a queueing system. The user has to provide a submission command for that, including any options which might be necessary. This submission script might not work with all queueing systems.
Project name
The user can enter a project name. This is used currently only for the job names of submitted jobs (-N option for queueing system).
7.5.5 Output
setup_init.py will create for each initial condition in the given range a directory whose names follow the format ICOND_%05i/, where %05i is the index of the initial condition padded with zeroes to 5 digits. Additionally, the directory ICOND_00000/ is created for the calculation of the excitation energies at the equilibrium geometry.
To each directory, the following files will be added:
- QM.in: Main input file for the interface, contains the geometry and the control keywords (to specify which quantities need to be calculated).
- run.sh: Run script, which can be started interactively in order to perform the ab initio calculation in this directory. Can also be adapted to a batch script for submission to a queue
- Interface-specific files: Usually a template file, a resource file, and an initial wave function.
The calculations in each directory can be simply executed by starting run.sh in each directory. In order to perform this task consecutively on a single machine, the script all_run.sh can be executed. The file DONE contains the progress of this calculation.
Alternatively, each run script can be sent to a queueing system (you might need to adapt this script to you cluster system).
Note that if reference overlaps were requested, the calculation in ICOND_00000/ must be finished before starting any of the other calculations.
In figure 7.1, the directory tree structure setup by setup_init.py is given.
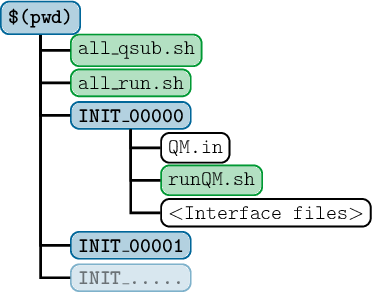
After all calculations are finished, excite.py can be used to collect the results.
7.6 Excitation Selection: excite.py
excite.py has two tasks: adding excited-state information to the initconds file, and deciding which excited state for which initial condition is a valid initial state for the dynamics.
7.6.1 Usage
The script is interactive, and can be started by simply typing
user@host> $SHARC/excite.py
7.6.2 Input
Initial condition file
Enter the path to the initial conditions file, to which excite.py will add excited-state information. This file can already contain excited-state information (in this case this information can be reused).
Generate excited state list
There are three possibilities to add excited-state information to the initconds file:
- generate a list of dummy excited states,
- read excited-state information from the output of the initial ab initio calculations (prepare the calculations with setup_init.py),
- keep the existing excited-state information in the initconds file.
The first option is mainly used if no initial ab initio calculations need to be performed (e.g., the initial state is known).
In order to use the second option, one should first setup initial excited-state calculations using setup_init.py (see 7.5) and run the calculations. excite.py can then read the output of the initial calculations and calculate excitation energies and oscillator strengths.
The third option can be used to reuse the information in the initconds file, e.g., to apply a different selection scheme to the states or to just read the number of states.
Path to ab initio results
If excite.py will read the excited-state information from the ab initio calculation results, here the user has to provide the path to the directory containing the ICOND_%05i subdirectories.
Number of states
If a dummy list of states will be generated, the user has to provide the number of states per multiplicity. Note that a singlet ground state has to be counted as well, e.g. if 4 singlet states are specified, the calculation will involve the S0, S1, S2 and S3. Also states of higher multiplicity can be given, e.g. doublet or triplet states (e.g., 2 2 1 for two singlets, two doublets and one triplet).
If the ab initio results are read the number of states will be automatically determined from the results.
Excited-state representation
When generating new lists of excited states (either dummy states or from ab initio results), the user has to specify the representation of the excited states (either MCH or diagonal representation). The MCH representation is spin-free, meaning that transition dipole moments are only allowed between states of the same multiplicity. For molecules without heavy atoms, this option is sufficient. For heavier atoms, the diagonal representation can be used, which includes the effects of spin-orbit coupling on the excitation energies and oscillator strengths.
Note, however, that excited-state selection with delta pulse excitation (option 3 under “Initial state selection”) should be carried out in the MCH representation if the ground state is not significantly spin-orbit-mixed.
When reading ab initio results, excite.py will diagonalize the Hamiltonian and transform the transition dipole matrices for each initial condition to obtain the diagonal representation.
When a dummy state list is generated, the representation will only be written to initconds.excited (but has no actual numeric effect for excite.py). Note that the representation which is declared in the initconds.excited file influences how SHARC determines the initial coefficients (see the paragraph on initial coefficients in 4.1.3).
Note that the representation cannot be changed if existing excited-state information is kept.
Hint: If the ICOND_%05i directories need to be deleted (e.g., due to disk space restrictions), making one read-out with excite.py for each representation and saving the results to two different files will preserve most necessary information.
Ionization probabilities
If excite.py detects that the ab initio results contain ionization probabilities, then those can be used instead of the transition dipole moments. Note that in this case the transition dipole moments are not written to the initconds.excited file.
Reference energy
excite.py can read the reference energy (ground state equilibrium energy) directly from the ab initio results. If the ab initio data is read anyways, excite.py already knows the relevant path. If a dummy list of states is generated, the user can provide just the path to the QM.out file of the ab initio calculation for the equilibrium geometry. Otherwise, excite.py will prompt the user to enter a reference energy manually (in hartree).
Initial state selection
Every excited state of each initial condition has a flag specifying it either as a valid initial state or not. excite.py has four modes how to flag the excited states:
- Unselect all excited states,
- User provides a list of initial states,
- States are selected stochastically based on excitation energies and oscillator strengths,
- Keep all existing flags.
The first option can be used if excite.py is only used to read the ab initio results for the generation of an absorption spectrum (using spectrum.py).
The second option can be used to directly specify a list of initial states, if the initial state is known (e.g., starting in the ground state and exciting with an explicit laser field). In this case, the given states of all initial conditions are flagged as initial states. This option is also useful if reference overlaps were computed (see 7.5.
The third option is only available if excited-state information exists (i.e., if no dummy list is generated). For details on the stochastic selection procedure, see section 8.9.
The fourth option can only be used if the existing state information is kept. In this case excite.py does nothing except counting the number of flagged initial states.
Excitation window
This option allows to exclude excited states from the selection procedure if they are outside a given energy window. This option is only available if excited state information exists, but not if a dummy list of states is generated (because the dummy states have no defined excitation energy).
For the stochastic selection procedure, states outside the excitation window do not count for the determination of pmax (see equation (8.45)). This allows to excite, e.g., to a dark nπ* state despite the presence of a much brighter ππ* state.
For the keep-flags option, this option can be used to count the number of excited states in the energy window.
Considered states
Here the user can specify the list of desired initial states.
If reference overlaps are present in the excitation calculations, then the user can choose to specify the initial state in terms of diabatized states (as defined by the overlap with the reference, where the diabatized states are identical to the computed states).
See section 8.9.1 for how the diabatization is carried out.
For the stochastic selection procedure, the user can instead exclude certain states from the procedure. Excluded states do not count for the determination of pmax (see equation (8.45)).
If the number of states per multiplicity is known, excite.py will print a table giving for each state index the multiplicity, quantum number and Ms value.
Random number generator seed
The random number generator in excite.py is used in the stochastic selection procedure. Instead of typing an integer, typing “!” will initialize the RNG from the system time. Note that this will not be reproducible, i.e. repeating the excite.py run with “!” as random seed will give a different selection in each run.
7.6.3 Matrix diagonalization
When using the diagonal representation, excite.py needs to diagonalize and multiply matrices. By default, the Python package NUMPY is used, if available. If the script does not find a NUMPY installation, it will use a small Fortran code which comes with the SHARC suite. In order for this to work, you need to set the environment variable $SHARC to the bin/ directory within your SHARC installation. See section 7.29 for more details.
7.6.4 Output
excite.py writes all output to a file <BASE>.excited, where <BASE> is the name of the initial conditions file used as input. The output file is also an initial conditions file, but contains additional information regarding the excited states, the reference energy and the representation of the excited states. An initial conditions file with excited-state information is needed for the final preparatory step: setting up the dynamics with setup_traj.py.
Additionally, spectrum.py can calculate absorption spectra from excited-state initial condition files.
7.6.5 Specification of the initconds.excited file format
The initial conditions files initconds and initconds.excited contain lists of initial conditions, which are needed for the setup of trajectories. An initial condition is a set of initial coordinates of all atoms and corresponding initial velocities of each atom, and optionally a list of excited state informations. In the following, the format of this file is specified.
The file contains of a header, followed by the body of the file containing a list of the initial conditions.
File header
An examplary header looks like:
SHARC Initial conditions file, version 0.2 <Excited> Ninit 100 Natom 2 Repr MCH Eref -0.50 Eharm 0.04 States 2 0 1 Equilibrium H 1.0 0.0 0.0 0.0 1.00782503 0.0 0.0 0.0 H 1.0 1.5 0.0 0.0 1.00782503 0.0 0.0 0.0
The first line must read SHARC Initial conditions file, version <VERSION>, with the correct version string followed. The string Excited is optional, and marks an initial conditions file as being an output file of excite.py (setup_traj.py will only accept files marked like this). The following lines contain:
- the number of initial conditions,
- the number of atoms,
- the electronic state representation (a string which is None, MCH or diag),
- the reference energy (hartree),
- the harmonic energy (zero point energy in the harmonic approximation, hartree),
- optionally the number of states per multiplicity.
After the header, first the equilibrium geometry is expected. It is demarked with the keyword Equilibrium, followed by natom lines, each specifying one atom. Unlike the actual initial conditions, the equilibrium geometry does not have a list of excited states or defined energies.
File body
The file body contains a list of initial conditions. Each initial condition is specified by a block starting with a line containing the string Index and the number of the initial condition. In the file, the initial conditions are expected to appear in order.
A block specifying an initial condition looks like:
Index 1 Atoms H 1.0 -0.02 0.0 0.0 1.00782503 -0.001 0.0 0.0 H 1.0 1.52 0.0 0.0 1.00782503 0.001 0.0 0.0 States 001 -0.49 -0.49 -0.16 0.0 -0.03 0.0 0.05 0.0 0.0 0.00 False 002 -0.25 -0.49 0.02 0.0 0.43 0.0 -1.77 0.0 6.5 0.53 True 003 -0.40 -0.49 0.00 0.0 0.00 0.0 0.00 0.0 2.5 0.00 False 004 -0.40 -0.49 0.00 0.0 0.00 0.0 0.00 0.0 2.5 0.00 False 005 -0.40 -0.49 0.00 0.0 0.00 0.0 0.00 0.0 2.5 0.00 False Ekin 0.004 a.u. Epot_harm 0.026 a.u. Epot 0.013 a.u. Etot_harm 0.030 a.u. Etot 0.018 a.u.
The formal structure of such a block is as follows. After the line containing the keyword Index and the index number, the keyword Atoms indicates the start of the list of atoms. Each atom is specified on one line:
- symbol,
- nuclear charge,
- x, y, z coordinate in Bohrs,
- atomic mass,
- x, y and z component of nuclear velocity in atomic units.
After the atom list, the keyword States indicates the list of electronic states. This list consists of one line per electronic state, but can be empty, if no information of the electronic states is available. Each line consists of:
- state number (starting with 1),
- state energy in Hartree,
- reference energy in Hartree (usually the energy of the lowest state),
- six numbers defining the transition dipole moment to the reference state (usually the lowest state),
- the excitation energy in eV,
- the oscillator strength,
- a string which is either True or False, specifying whether the electronic state was selected by excite.py as initial electronic state.
The transition dipole moments are specified by six floating point numbers, which are real part of the x component, imaginary part of the x component, then the real and imaginary parts for the y and finally the z component (the transition dipole moments can be complex in the diagonal representation).
The electronic state list is terminated with the keyword Ekin, which at the same time gives the kinetic energy of all atoms. The remaining entries give the potential energy in the harmonic approximation and the actual potential energy, as well as the total energy.
7.7 Setup of Trajectories: setup_traj.py
This interactive script prepares the input for the excited-state dynamics simulations with SHARC. It works similarly to setup_init.py, reading an initial conditions file, prompting the user for a number of input parameters, and finally prepares one directory per trajectory. However, the setup_traj.py input section is noticeably longer, because most options for the SHARC dynamics are covered.
7.7.1 Input
Initial conditions file
Please be aware that setup_traj.py needs an initial conditions file generated by excite.py (files generated by wigner.py, amber_to_initconds.py, or sharctraj_to_initconds.py are not allowed). The script reads the number of initial states, the representation, and the reference energy automatically from the file.
Number of states
This is the total number of states per multiplicity included in the dynamics calculation. Affects the keyword nstates in the SHARC input file.
Only advanced users should use here a different number of states than given to setup_init.py. In this case, the excited-state information in the initial conditions file might be inconsistent. For example, if 10 singlets and 10 triplets were included in the initial calculations, but only 5 singlets and 5 triplets in the dynamics, then the sixth entry in the initial conditions file corresponds to S5, while setup_traj.py assumes the sixth entry to correspond to T1.
Active states
States can be frozen for the dynamics calculation here. See section 8.2 for a general description of state freezing in SHARC. Only the highest states in each multiplicity can be frozen, it is not possible to, e.g., freeze the ground state in simulations where ground state relaxation is negligible. Affects the keyword actstates.
Contents of the initial conditions file
Optionally, a map of the contents of the initial conditions file can be displayed during the execution of setup_traj.py, showing for each state which initial conditions were selected (and which initial conditions do not have the necessary excited-state information). For each state, a table is given, where each symbol represents one initial condition. A dot “.” represents an initial condition where information about the current excited state is available, but which is not selected for dynamics. A hash mark “#” represents an initial condition which is selected for dynamics. A question mark “?” represents initial conditions for which no information about the excited state is available (e.g. if the initial excited-state calculation failed). The tutorial shows an example of this output.
The content of the initial conditions file is also summarized in a table giving the number of initial conditions selected per state.
Initial states for dynamics setup
The user has to input all states from which trajectories should be launched. The numbers must be entered according to the above table giving the number of selected initial conditions per state. It is not allowed to specify inactive states as initial states. The script will give the number of trajectories which can be setup with the specified set of states. If no trajectories can be setup, the user has to specify another set of initial states. The initial state will be written to the SHARC input, specified in the same representation as given in the initial conditions file. The initial coefficients will be determined automatically by SHARC, according to the description in section 4.1.3.
Starting index for dynamics setup
Specifies the first initial condition within the initial condition file to be included in the setup. This is useful, for example, if the user might setup 50 trajectories starting with index 1. setup_traj.py reports afterwards the last initial condition to be used for setup, e.g. index 90. Later, the user can setup additional trajectories, starting with index 91.
Random number generator seed
The random number generator in setup_traj.py is used to randomly generate RNG seeds for the SHARC input. Instead of typing an integer, typing “!” will initialize the RNG from the system time. Note that this will not be reproducible, i.e. repeating the setup_traj.py run (with the same input) with “!” as random seed will give for the same trajectories different RNG seeds. Affects the keyword RNGseed.
Interface
In this point, choose any of the displayed interfaces to carry out the ab initio calculations. Enter the corresponding number. The choice of the interface influences some dynamics options which can be set in the next section of the setup_traj.py input.
Simulation Time
This is the maximum time that SHARC will run the dynamics simulation. If trajectories need to be run for longer time, it is recommended to first let the simulation finish. Afterwards, increase the simulation time in the corresponding SHARC input file (keyword tmax) and add the restart keyword (also make sure that the norestart keyword is not present). Then the simulation can be restarted by running again the run.sh script. Sets the keyword tmax in the SHARC input files.
Simulation Timestep
This gives the time step for the dynamics. The on-the-fly ab initio calculations are performed with this time step, as is the propagation of the nuclear coordinates. A shorter time step gives more accurate results, especially if light atoms (hydrogen) are subjected to high kinetic energies or steep gradients. Of course a shorter time step is computationally more expensive. A good compromise in many situations is 0.5 fs. Sets the keyword stepsize in the SHARC input files.
Number of substeps
This gives the number of substeps for the interpolation of the Hamiltonian for the propagation of the electronic wave function. Usually, 25 substeps are sufficient. In cases where the diagonal elements of the Hamiltonian are very large (very large excitation energies or a badly chosen reference energy) more substeps are necessary. Sets the keyword nsubsteps in the SHARC input files.
Prematurely terminate trajectories
Usually, trajectories which relaxed to the ground state do not recross to an excited state, but vibrate indefinitely in the ground state. If the user is not interested in these vibrations, such trajectories can be terminated prematurely in order to save computational resources. A threshold of 10-20 fs is usually a good choice to safely detect ground state relaxation. Sets the keyword killafter in the SHARC input files.
Representation for the dynamics
Either the diagonal representation can be chosen (by typing “yes“) to perform dynamics with the SHARC methodology, or the dynamics can be performed on the MCH states (spin-diabatic dynamics [26], FISH [25]). Sets the keyword surf in the SHARC input files.
Spin-orbit couplings
If more than just singlet states are requested, the script asks whether spin-orbit couplings should be computed. If the chosen interface cannot provide spin-orbit couplings, this question is automatically answered.
Non-adiabatic couplings
Electronic propagation can be performed with temporal derivatives, nonadiabatic coupling vectors or overlap matrices (Local diabatization). Enter the corresponding number. Note that depending on the chosen interface, some options might not be available, as displayed by setup_traj.py. Also note that currently, no interface can provide temporal derivatives (because their computation involves calculating the overlap matrix and then local diabatization can be done instead). Sets the keyword coupling in the SHARC input files.
If nonadiabatic coupling vectors are chosen, the user is asked whether overlap matrices should be computed anyways to provide wave function phase information. As the overlap calculations are usually fast compared to other steps, this is recommended.
Gradient transformation
The nonadiabatic coupling vectors can be used to correctly transform the gradients to the diagonal representation. If nonadiabatic coupling vectors are used anyways, this option is strongly recommended, since it gives more accurate gradients for no additional cost. Sets the keyword gradcorrect in the SHARC input files. If the dynamics uses the MCH representation, this question is not asked.
Surface hop treatment
This option determines how the total energy is conserved after a surface hop and whether frustrated hops lead to reflection. Sets the keywords ekincorrect and reflect_frustrated in the SHARC input files.
Decoherence correction
For most applications, a decoherence correction should be enabled. This controls the decoherence_scheme (and decoherence_param keywords in the SHARC input files.
Note that setup_traj.py does not allow to modify the α parameter for the energy-based decoherence (keyword decoherence_param). In order to change decoherence_param, the user has to manually edit the SHARC input files.
Surface hopping scheme
Choose one of the available schemes to compute the hopping probabilities or turn off hopping.
Scaling and Damping
These two prompts set the keywords scaling and damping in the SHARC input files. The scaling parameter has to be positive, and the damping parameter has to be in the interval [0,1].
Atom masking
In some cases, the script will ask to specify the atoms to which decoherence/rescaling/reflection should be applied.
See section 4 for explanations (keyword atommask).
Gradient and nonadiabatic coupling selection
For dynamics in the MCH representation, selection of gradients is used by default, and only one gradient (of the current state) is calculated. Selection of nonadiabatic couplings is only relevant if they are used (for propagation, gradient correction or rescaling of the velocities after a surface hop). For the selection threshold, usually 0.5 eV is sufficient, except if spin-orbit coupling is very strong and hence the gradients mix strongly.
Sets the keywords grad_select and nac_select in the SHARC input files.
Laser file
The user can specify to use an external laser field during the dynamics, and has to provide the path to the laser file (see section 7.8 and 4.5). setup_traj.py will check whether the number of steps and the time steps are compatible to the dynamics. If the interface can provide dipole moment gradients, setup_traj.py will also ask whether dipole moment gradients should be included in the simulations.
Dyson norm calculation
If the interface is compatible, the user can request that Dyson norms are calculated on-the-fly. This option is only asked if Dyson norms can be computed (i.e., if states are present which differ by one electron, e.g., singlets and doublets).
THEODORE calculations
If the interface is compatible, the user can request that THEODORE is run on-the-fly.
7.7.2 Interface-specific input
This input section is basically the same as for setup_init.py (section 7.5.3 and following sections). Note that for the dynamics simulations an initial wave function file is even more strongly recommended than for the initial excited-state calculations.
7.7.3 Output control
setup_traj.py will ask a number of questions regarding the content of the output.dat file, specifically about writing gradients, nonadiabatic coupling vectors, properties (1D and 2D), and overlap matrices to this file.
Note that this is only possible if these quantities are actually calculated; otherwise, sharc.x will ignore these requestes.
7.7.4 Run script setup
Also this input section is very similar to the one in setup_init.py (see section 7.5).
7.7.5 Output
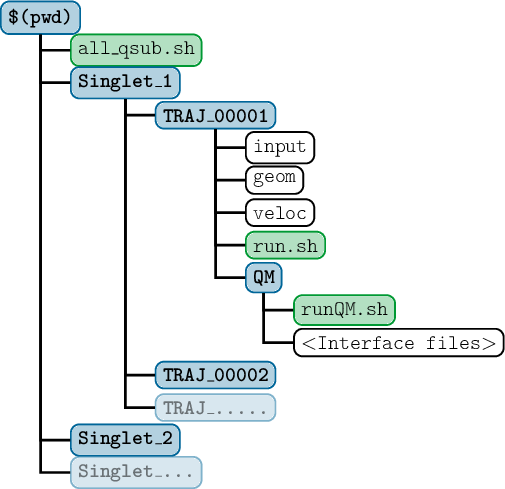
setup_traj.py will create for each initial state a directory where all trajectories starting in this state will be put. If the initial conditions file specified that the initial conditions are in the MCH representation, then the initial states will be assumed to be in the MCH representation as well. In this case, the directories will be named Singlet_0, Singlet_1, …, Doublet_0, Triplet_1, … If the initial states are in the diagonal representation, then the directories are simply called X_1, … since they do not have a definite spin.
In each directory, subdirectories called TRAJ_%05i are created, where %05i is the initial condition index, padded to 5 digits with zeroes. In each trajectory’s directory, an SHARC input file called input will be created, which contains all the dynamics options chosen during the setup_traj.py run. Also, files geom and veloc will be created. For trajectories setup with setup_traj.py, the determination of the initial wave function coefficients is done by SHARC.
Furthermore, in each trajectory directory a subdirectory QM is created, where the runQM.sh script containing the call to the interface is put. In the directory QM also all interface-specific input files will be copied.
For each trajectory, a run.sh script will be created, which can be executed to run the dynamics simulation. You might need to adapt the run script to your cluster setup.
setup_traj.py also creates a script all_run_traj.sh, which can be used to execute all trajectories sequentially.
Note that this is intended for small test trajectories, and should not be used for expensive production trajectories.
For the latter, setup_traj.py can optionally create a script all_qsub_traj.sh, which can be executed to submit all trajectories to a queueing system. You might need to adapt also this script to your cluster setup.
The full directory structure created by setup_traj.py is given in figure 7.2.
7.8 Laser field generation: laser.x
The Fortran code laser.x can generate files containing laser fields which can be used with SHARC. It is possible to superimpose several lasers, use different polarizations and apply a number of chirp parameters.
7.8.1 Usage
The program is simply called by
user@host> $SHARC/laser.x
It will interactively ask for the laser parameters. After input is complete, it writes the laser field to the file laser in the format which SHARC expects (see 4.5).
Similar to the interactive Python scripts, laser.x will also write the user input to KEYSTROKES.laser. After modifying this file, it can be used to directly execute laser.x without doing the interactive input again:
user@host> $SHARC/laser.x < KEYSTROKES.laser
7.8.2 Input
The first four options are global and need to be entered only once, all remaining input options need to be given for every laser pulse. For the definition of laser fields see section 8.16.
Number of lasers
Any number of lasers can be used. The output file will contain the sum of all laser pulses defined.
Real-valued field
If this is true, the output file will only contain the real parts of the laser field, while the columns defining the imaginary part of the field will be zero. Note, however, that SHARC will anyways only use the real part of the field in the simulations.
Time interval and steps
The definitions of the starting time, end time and time step of the laser field must exactly match the simulation time and time substeps of the SHARC simulation. Note, that the laser field must always start at t=0 fs to be used with SHARC. The end time for the laser field must therefore coincide with the total simulation time given in the SHARC input. The number of time steps for the laser field is ttotal/∆tsub +1.
Files for debugging
This option is normally not needed, and can be set to False. If set to True, the chirped and unchirped laser fields in both time and frequency domain will be written to files called DEBUG_... .
Polarization vector
The polarization vector p (will be normalized).
Type of envelope
There are two options possible for the envelope function E(t), either a Gaussian envelope or a sinusoidal one (see 8.16).
Field strength
There are two input lines for the field strength E0, the first defining the unit in which the field strength is defined, the second gives the corresponding number. Field strength can be read in in GV/m, TW/cm−2 or atomic units.
FWHM and time intervals
This option depends on the type of envelope chosen. While in both cases all 5 numbers need to be entered, for a Gaussian pulse only the first and third number have an effect. For a sinusoidal pulse all but the first number has an effect.
For a Gaussian pulse, the first argument corresponds to FWHM in equation (8.94) and the third argument to tc in (8.93).
For a sinusoidal pulse, the second, third, fourth and fifth argument correspond to t0, tc, tc2 and te, respectively, in equation (8.95).
Central frequency
There are two input lines for the central frequency ω0. The first defines the unit (wavelength in nm, energy in eV, or atomic units). The second line gives the value.
Phase
The total phase ϕ is given in multiples of π. For example, the input “1.5” gives a phase of [(3π)/2].
Chirp parameters
There are four lines giving the chirp parameters b1, b2, b3 and b4. See equation (8.97) for the meaning of these parameters.
7.9 Calculation of Absorption Spectra: spectrum.py
Aside from setting up trajectories, the initconds.excited files can also be used to generate absorption spectra based on the excitation energies and oscillator strengths in the file. The script spectrum.py calculates Gaussian, Lorentzian, or Log-normal convolutions of these data in order to obtain spectra. See section 8.1 for further details.
spectrum.py evaluates the absorption spectrum on a grid for all states it finds in an initial conditions file. Using command-line options, some initial conditions can be omitted in the convolution, see table 7.5.
7.9.1 Input
The script is executed with the initial conditions file as argument:
user@host> $SHARC/spectrum.py [OPTIONS] initconds.excited
The script accepts a number of command-line options, which are given in table 7.5.
| Option | Description | Default |
| -h | Display help message and quit. | – |
| -o FILENAME | Output filename for the spectrum | spectrum.out |
| -n INTEGER | Number of grid points | 500 |
| -e FLOAT FLOAT | Energy range (eV) for the spectrum | 1 to 10 eV |
| -i INTEGER INTEGER | Index range for the initial conditions | 1 to 1000 |
| -f FLOAT | FWHM (eV) for the spectrum | 0.1 eV |
| -G | Gaussian convolution | Gaussian |
| -L | Lorentzian convolution | Gaussian |
| -N | Log-normal convolution | Gaussian |
| -s | Use only selected initial conditions | Use all |
| -l | Make a line spectrum | Convolution |
| -D | Compute density of states (ignore fosc) | Compute absorption |
| -gnuplot FILENAME | Write a GNUPLOT script | No GNUPLOT script |
| -B INTEGER | Perform B bootstrapping cycles (error estimation) | 0 |
| -b FILENAME | Output filename for bootstrapping | spectrum_bootstrap.out |
| -r INTEGER | Seed for random number generator (for bootstrap) | 16661 |
7.9.2 Output
The script writes the absorption spectrum to a file (by default spectrum.out). Using the -o option, the user can redirect the output to a suitable file. The output is a table containing n+2 columns, where n is the number of states found in the initial conditions file. The first column gives the energy in eV, within the given energy interval. In columns 2 to n+1 the state-wise absorption spectra are given. The last column contains the total absorption spectrum, i.e., the sum over all states. The table has ngrid+1 rows. For line spectra the output format is exactly the same, however, the file will contain one row for each excited state of each initial condition in the initial conditions file. If density of states is computed, the script replaces the oscillator strength by a factor of 1 for all states.
Additionally, the script writes some information about the calculation to standard output, among these the maximum of the spectrum, which can be used in order to normalize the spectrum. The reported maximum is simply the largest value in the last column of the spectrum.
If requested, the script generates a GNUPLOT script, which can be used to directly plot the spectrum.
7.9.3 Error Analysis
The shape of the spectrum is strongly influenced by the number of initial conditions included and by the width of the broadening function (FWHM).
In principle, the FWHM of the broadening function should be as small as possible and the number of initial conditions extremely large, in order to obtain a correctly sampled spectrum.
In reality, if only few initial conditions were considered, the FWHM should be chosen large enough to smooth out any artifical structure of the spectrum arising solely from the small sample size.
In order to estimate whether the number of initial conditions and the FWHM are well-chosen, spectrum.py can compute error estimates for the total absorption spectrum.
This estimate is computed by a bootstrapping procedure (similar to the one used in bootstrap.py).
In order to use it, use the -B option with a positive integer argument (the default is zero, and hence no bootstrapping is performed).
The procedure will generate a second output file, called spectrum_bootstrap.out by default.
It contains in the first column the energy in eV, in the second the geometric average spectrum from all bootstrap cycles, in column 3 and 4 the positive and negative errors of the spectrum, and in all further columns the individual spectra obtained in the bootstrap cycles.
In gnuplot, in order to plot the average spectrum and the upper and lower error bounds, plot u 1:2, u 1:($2+$3), and u 1:($2+$4).
A suitable procedure is to start with a rather small FWHM, compute the spectrum with errors, and if the errors are unsatisfactorily large, increase stepwise the FWHM.
Note that the bootstrapping estimate will give very small errors if the FWHM is very large-even though the actual spectrum can look very different in this case.
7.10 File transfer: retrieve.sh
Usually, SHARC will run on some temporary directory, and not in the directory where the trajectories have been submitted from. The shell script retrieve.sh is a simple scp wrapper, which can be executed (in a directory where a trajectory has been sent from) in order to retrieve the output files of this trajectory. This might not work for every cluster setup.
It relies on the presence of the file host_infos. All trajectories set up with setup_traj.py create this file after the trajectory has been started with run.sh. retrieve.sh reads host_infos to determine the hostname and working directory of the trajectory and then uses scp to retrieve the output and restart files.
The script can be called with the option “-lis” in order to only retrieve the output.lis file, but not the other output files.
If the script is called with the option “-res” then also the restart files and the content of the restart/ directory are copied.
It is advisable to configure public-key authentification for the hosts running the trajectories, so that not for every execution of retrieve.sh a password has to be entered.
7.11 Data Extractor: data_extractor.x
The data_extractor.x is the primary tool to extract useful, tabular data from the output.dat file that is produced by sharc.x.
The produced files can then be further processed, e.g., by plotting them or by computing ensemble statistics with data_collector.py (section 7.25).
7.11.1 Usage
The data_extractor.x is a command line tool, and is called with the output.dat file as an argument, and possibly with some options.
user@host> $SHARC/data_extractor.x [options] output.dat
The program will create a directory output_data/ in the current working directory (not necessarily in the directory where output.dat resides). In this directory, several files are written, containing, e.g., the potential energies depending on time, populations depending on time, etc.
Which files are created can be controlled with the command line options, which are summarized in Table 7.6. For most applications, using the -xs or -s flags should be sufficient. The default is equivalent to -s.
Note that some options might not be available if the necessary data is not written to output.dat (see write options in Table 4.1).
The program will extract the complete output.dat file until it reaches the EOF.
The data_extractor.x program will automatically detect the format of the output.dat file (the first SHARC release had a different file format than the more recent SHARC releases).
7.11.2 Output
After the program finishes, the directory output_data/ contains a number of files. In each file, the number of columns is dependent in the total number n of states i ∈ {1…n}. The content of the files is listed in Table 7.7.
The file expec.out contains the information of energy.out, spin.out and fosc.out in one file. The content of expec.out can be conveniently plotted by using make_gnuscript.py (section 7.14) to generate a GNUPLOT script.
| Option | Description | Default |
| -h | Display help message and quit. | – |
| -f | File name (can also be given without file name) | File name must be given |
| -sk | skip parsing of geom., vel., grad., NAC. | False |
| -e | Write energy.out | True |
| -d | Write fosc.out | True |
| -da | Write fosc_act.out | True |
| -sp | Write spin.out | True |
| -cd | Write coeff_diag.out, coeff_class_diag.out, coeff_mixed_diag.out |
True |
| -cm | Write coeff_MCH.out, coeff_class_MCH.out, coeff_mixed_MCH.out |
True |
| -cb | Write coeff_diab.out, coeff_class_diab.out, coeff_mixed_diab.out |
True (if overlaps present) |
| -p | Write prob.out | True |
| -x | Write expec.out | True |
| -xm | Write expec_MCH.out | True |
| -id | Write ion_diag.out | False |
| -im | Write ion_MCH.out | False |
| -dd | Write dip_mom_diag.out | False |
| -xs | -e, , -d, , -cd, , -cm, , -p, , -x | |
| -s | -sp, , -xm, , -cb, , -da plus -xs | Default |
| -l | -id, , -im plus -s | |
| -xl | -dd plus -l (i.e., all) |
|
Table 7.7: Content of the files written by data_extractor.x. n is the total number of states, j is a state index (j ∈ {1..n}), and α is the active state.
|
||||
| File | # Columns | Columns | ||
|
energy.out |
4+n | 1 | Time t (fs) | |
| 2 | Kinetic energy (eV) | |||
| 3 | Potential energy (eV) of active state (diagonal) | |||
| 4 | Total energy (eV) | |||
| 4+j | Potential energy (eV) of state j (diagonal) | |||
| fosc.out | 2+n | 1 | Time t (fs) | |
| 2 | Oscillator strength from lowest to active state (diagonal) | |||
| 2+j | Oscillator strength from lowest state to state j (diagonal) | |||
| fosc_act.out | 1+2n | 1 | Time t (fs) | |
| 1+j | Ej−Eactive (in eV, diagonal) | |||
| 1+n+j | Oscillator strength from active state to state j (diagonal) | |||
| spin.out | 2+n | 1 | Time t (fs) | |
| 2 | Total spin expectation value of active state | |||
| 2+j | Total spin expectation value of state j | |||
| coeff_diag.out | 2+2n | 1 | Time t (fs) | |
| 2 | Norm of wave function ∑j |cjdiag|2 | |||
| 1+2j | ℜ(cjdiag) | |||
| 2+2j | ℑ(cjdiag) | |||
| coeff_class_diag.out | 2+n | 1 | Time t (fs) | |
| 2 | 1 | |||
| 2+j | δjα | |||
| coeff_mixed_diag.out | 2+n | 1 | Time t (fs) | |
| 2 | 1 | |||
| 2+j | δjα | |||
| coeff_MCH.out | 2+2n | 1 | Time t (fs) | |
| 2 | Norm of wave function ∑j |cjMCH|2 | |||
| 1+2j | ℜ(cjMCH) | |||
| 2+2j | ℑ(cjMCH) | |||
| coeff_class_MCH.out | 2+n | 1 | Time t (fs) | |
| 2 | 1 | |||
| 2+j | |Ujα|2 | |||
| coeff_mixed_MCH.out | 2+n | 1 | Time t (fs) | |
| 2 | 1 | |||
| 2+j | |Ujα|2+∑k,l2ℜ(UjkU*jlcdiagkcdiag*l) | |||
| coeff_diab.out | 2+2n | 1 | Time t (fs) | |
| 2 | Norm of wave function ∑j |cjdiab|2 | |||
| 1+2j | ℜ(cjdiab) | |||
| 2+2j | ℑ(cjdiab) | |||
| coeff_class_diab.out | 2+2n | 1 | Time t (fs) | |
| 2 | 1 | |||
| 2+j | |Tjα|2 | |||
| coeff_mixed_diab.out | 2+2n | 1 | Time t (fs) | |
| 2 | 1 | |||
| 2+j | |Tjα|2+∑k,l2ℜ(TjkT*jlcdiagkcdiag*l) | |||
| prob.out | 2+n | 1 | Time t (fs) | |
| 2 | Random number from surface hopping | |||
| 2+j | Cumulated hopping probability ∑k=1j Pk | |||
| expec.out | 4+3n | 1 | Time t (fs) | |
| 2 | Kinetic energy (eV) | |||
| 3 | Potential energy (eV) of active state (diagonal) | |||
| 4 | Total energy (eV) | |||
| 4+j | Potential energy (eV) of state j (diagonal) | |||
| 4+n+j | Total spin expectation value of state j (diagonal) | |||
| 4+2n+j | Oscillator strength of state j (diagonal) | |||
| expec_MCH.out | 4+3n | 1 | Time t (fs) | |
| 2 | Kinetic energy (eV) | |||
| 3 | Potential energy (eV) of approximate active state (MCH) | |||
| 4 | Total energy (eV) | |||
| 4+j | Potential energy (eV) of state j (MCH) | |||
| 4+n+j | Total spin expectation value of state j (MCH) | |||
| 4+2n+j | Oscillator strength of state j (MCH) | |||
| ion_diag.out | 4+3n | 1 | Time t (fs) | |
| 1+j | Ej−Eactive (in eV, diagonal) | |||
| 1+n+j | Dyson norm from active state to state j (diagonal) | |||
| ion_MCH.out | 4+3n | 1 | Time t (fs) | |
| 1+j | Ej−Eapproximate active (in eV, mCH) | |||
| 1+n+j | Dyson norm from approximate active state to state j (MCH) | |||
| dip_mom_diag.out | Formatted like a minimal output.dat | |||
| file containing the dipole moment matrices | ||||
| in diagonal representation. | ||||
7.12 Data Extractor for NetCDF: data_extractor_NetCDF.x
This program has the same function as the data_extractor.x.
While the latter acts on ASCII-formatted output.dat files, the data_extractor_NetCDF.x reads only the header from output.dat, but the time step data from output.dat.nc.
This file is obtained by setting output_format to ascii in the SHARC input file.
For more details, see Section 5.4.
Note that this program currently does not support a few options of the data_extractor.x.
In particular, the options -sk, -dd, -id, and -im are ignored and no corresponding output is produced.
Using the -xyz flag, the data_extractor_NetCDF.x can be used to write an output.xyz file from the NetCDF data file.
7.12.1 Usage
The data_extractor_NetCDF.x is used in the same way as data_extractor.x:
user@host> $SHARC/data_extractor_NetCDF.x [options] output.dat
Note that both output.dat and output.dat.nc need to be present.
The file name of output.dat.nc is hardcoded, if your file is called differently, you should set a symbolic link.
7.12.2 Output
Same as data_extractor.x.
7.13 Data Converter for NetCDF: data_converter.x
This program can be used to convert an output.dat file into a NetCDF file (output.dat.nc).
This significantly reduces the size of the file, and allows deleting the output.xyz file (its content will be in the NetCDF file).
7.13.1 Usage
The data_converter.x usage is very simple:
user@host> $SHARC/data_converter.x output.dat
Note that the data_converter.x does not modify the output.dat file.
Hence, in order to save disk space, remove the data (below the header) afterwards:
user@host> sed -i '1,/End of header array data/!d' output.dat
7.13.2 Output
The program writes a file called output.dat.nc.
This file can be extracted as usual with data_extractor_NetCDF.x (see section 7.12).
7.14 Plotting the Extracted Data: make_gnuscript.py
The contents of the output files of data_extractor.x can be plotted with GNUPLOT. In order to quickly generate an appropriate GNUPLOT script, make_gnuscript.py can be used. The usage is:
user@host> $SHARC/make_gnuscript.py <S> [<D> [<T> [<Q> ... ] ] ]
make_gnuscript.py takes between 1 and 8 integers as command-line arguments, specifying the number of singlet, doublet, triplet, etc. states. It writes an appropriate GNUPLOT script to standard out, hence redirect the output to a file, e.g.:
user@host> $SHARC/make_gnuscript.py 3 0 2 > gnuscript.gp
Then, GNUPLOT can be run in the output_data directory of a trajectory:
user@host> gnuplot gnuscript.gp
This can also be accomplished in one step using a pipe, e.g.:
user@host> $SHARC/make_gnuscript.py 3 0 2 | gnuplot
The created plot script generates four different plots (press ENTER in the command-line where you started GNUPLOT to go to the next plot). The first plot shows the potential energy of all states in the dynamics over time in the diagonal representation. The currently occupied state is marked with black circles. A thin black line gives the total energy (sum of the kinetic energy and the potential energy of the currently occupied state). Each state is colored, with one color as contour and one color at the core of the line. The contour color represents the total spin expectation value of the state. The core color represents the oscillator strength of the state with the lowest state. See figure 7.3 for the relevant color code.
Note that by definition the “oscillator strength” of the lowest state with itself is exactly zero, hence the lowest state is also light grey. This dual coloring allows for a quick recognition of different types of states in the dynamics, e.g. singlets vs. triplets or nπ* vs. ππ* states.
The second plot shows the same data again, but using relative energies such that the energy of the lowest state is zero.
The third plot shows the population |ciMCH|2 of the MCH electronic states over time. The line colors are auto-generated in order to give a large spread of all colors over the excited states, but the colors might be sub-optimal, e.g. for printing. In this cases, the user should manually adjust the colors in the generated script.
The fourth plot shows the population |cidiag|2 of the diagonal electronic states over time. These are the populations which are actually used for surface hopping. However, since these states are spin-mixed, it is usually difficult to interpret these populations.
The fifth plot shows the surface hopping probabilities over time. The plot is setup in such a way that the visible area corresponding to a certain state is proportional to the probability to hop into the state. Hence, if for a given time step the random number (black circles) lies within a colored area, a surface hop to the corresponding state is performed.
7.15 Ensemble Diagnostics Tool: diagnostics.py
The purpose of this script is to automatize the critical step of checking the trajectories in an ensemble for sanity before beginning the ensemble analysis.
The tool can check several different aspects of the trajectories.
First, it checks whether all relevant output files of the trajectories are present, and if they are complete and consistent (e.g., no missing lines due to network/file system problems).
Second, it checks simulation progress and status (e.g., whether the trajectory is running, crashed, finished, or stopped).
Third, it can check several energy-related requirements: total energy conservation, smoothness of kinetic and potential energy, and hopping energy differences.
It also checks for conservation of total population, and for trajectories using local diabatization also intruder states are checked.
Note that the diagnostics script can also be used to automatically run the data_extractor.x for all trajectories.
Also note that diagnostics.py will not work if the printlevel in the SHARC trajectories was lower than 2.
7.15.1 Usage
The script is interactive, simply start it with no command-line arguments or options:
user@host> $SHARC/diagnostics.py
7.15.2 Input
Paths to trajectories
First the script asks the user to specify all directories for whose content the analysis should be performed. Enter one directory path at a time, and finish the directory input section by typing “end“. Please do not specify each trajectory directory separately, but specify their parent directories, e.g. the directories Singlet_1 and Singlet_2. diagnostics.py will automatically include all trajectories contained in these directories.
Unlike the ensemble analysis scripts (these are populations.py, transition.py, crossing.py, trajana_essdyn.py, trajana_nma.py, and data_collector.py, see below), diagnostics.py ignores files which indicate the status of a trajectory (CRASHED, RUNNING, DONT_ANALYZE) and carries out the diagnostics routines as long as it identifies a directory as a SHARC trajectory.
Settings
The settings for the diagnostics run can be modified with a simple menu, which can be navigated with the commands show, help, end, and where the settings can be modified with <key> <value> (e.g., hop_energy 0.2 sets the corresponding option to 0.2 eV).
A list of the settings is given in Table 7.8.
Generally, the keywords missing_output, missing_restart, and normal_termination should always be left at True, since checking them is cheap and the obtained information is important.
Note that data_extractor.x is always run for all trajectories, except if output.dat is older than the files in output_data/.
During the check of each trajectory, output.lis, output_data/energies.out, and output_data/coeff_diag.out are furthermore checked for missing time steps.
| Key | Value | Explanation |
| missing_output | Boolean | Checks if öutput.lis”, öutput.log”, öutput.xyz”, öutput.dat” are existing. Setting to False only suppresses output, but files are always checked. |
| missing_restart | Boolean | Checks if “restart.ctrl”, “restart.traj”, “restart/” are existing. Files are not checked if set to False. |
| normal_termination | Boolean | Checks for status of trajectory: |
| RUNNING: no finish message in output.log, last step started recently. | ||
| STUCK: no finish message in output.log, last step started long ago. | ||
| CRASHED: error message in output.log. | ||
| FINISHED: finish message in output.log. | ||
| FINISHED (stopped by user): finished due to STOP file. | ||
| etot_window | Float | Maximum permissible drift (along full trajectory) in the total energy (in eV). |
| etot_step | Float | Maximum permissible total energy difference between two successive time steps (in eV). |
| epot_step | Float | Maximum permissible active state potential energy difference between two successive time steps (in eV). Not checked for time steps where a hop occurred. |
| ekin_step | Float | Maximum permissible kinetic energy difference between two successive time steps (in eV). |
| pop_window | Float | Maximum permissible drift in total population. |
| hop_energy | Float | Maximum permissible change in active state energy during a surface hop (in eV). |
| intruders | Boolean | Checks if intruder state messages in öutput.log” refer to active state. |
| always_update | Boolean | Run the data_extractor.x always, even if output.dat is older than the produced files. |
| extractor_mode | String | Controls command line flags for the data_extractor.x: |
| xs: Uses the -xs flag. | ||
| s: Uses the -s flag. | ||
| l: Uses the -l flag. | ||
| xl: Uses the -xl flag. | ||
| dont: data_extractor.x is never run (this leads to incomplete diagnostics, but is very fast). |
Trajectory Flagging
diagnostics.py determines for each trajectory a “maximum usable time” value (Tmu).
This value is either the total simulation time or the time when the first violation (problems with time step consistency, total energy conservation, potential/kinetic energy smoothness, hopping energy restriction, or intruder states) in the trajectory appeared.
The script prints the Tmu values for all trajectories at the end.
The user can then give a threshold for Tmu, so that diagnostics.py excludes all trajectories with values smaller than the threshold from analysis (the script will create a file DONT_ANALYZE in the directory of each affected trajectory).
In this way it is possible to perform ensemble analysis for a given simulation length while ignoring problematic trajectories.
When choosing the threshold for Tmu, keep in mind that a compromise usually has to be made.
A small value of the threshold will mean that many trajectories are admitted for analysis (because problems occurring late do not matter), giving good statistics, but that the analysis can only be carried out for the first part of the simulation time.
On the other hand, choosing a large threshold allows analysis of a satisfactory simulation time, but only few trajectories will be included in the analysis (only the ones where no problems occurred for many time steps).
It is advisable that the chosen threshold value is used as input for the ensemble analysis scripts which ask for a maximum analysis time (populations.py, transition.py, crossing.py, trajana_essdyn.py, trajana_nma.py).
7.16 Calculation of Ensemble Populations: populations.py
For an ensemble of trajectories, usually one of the most relevant results are ensemble-averaged populations. The interactive script populations.py collects these populations from a set of trajectories.
Different methods to obtain populations or quantities approximating populations can be collected, as described below.
7.16.1 Usage
The script is interactive, simply start it with no command-line arguments or options:
user@host> $SHARC/populations.py
Depending on the analysis mode (see below) it might be necessary to run data_extractor.x for each trajectory prior to running populations.py (but populations.py can also call data_extractor.x for each subdirectory, if desired).
Paths to trajectories
First, the script asks the user to specify all directories for whose content the analysis should be performed. Enter one directory path at a time, and finish the directory input section by typing “end“. Please do not specify each trajectory directory separately, but specify their parent directories, e.g. the directories Singlet_1 and Singlet_2. populations.py will automatically include all trajectories contained in these directories.
If you want to exclude certain trajectories from the analysis, it is sufficient to create an empty file called CRASHED or RUNNING in the corresponding trajectory directory. populations.py will ignore all directories containing one of these files. The file name is case insensitive, i.e., also files like crashed or even cRasHED will lead to the trajectory being ignored.
Additionally, populations.py will ignore trajectories with a DONT_ANALYZE file from diagnostics.py.
Analysis mode
Using populations.py, there are two basic ways in obtaining the excited-state populations. The first way is to count the number of trajectories for which a certain condition holds. For example, the number of trajectories in each classical state can be obtained in this way. However, it is also possible to count the number of trajectories for which the total spin expectation value is within a certain interval.
The second way to obtain populations is to obtain the sum of the absolute squares of the quantum amplitudes over all trajectories. Table 7.9 contains a list of all possible analysis modes.
| Mode | Description | From which file? | Extract? |
| 1 | For each diagonal state count how many trajectories have this state as active state. | output.lis | No |
| 2 | For each MCH state count how many trajectories have this state as approximate active state (see section 8.23.1). | output.lis | No |
| 3 | For each MCH state count how many trajectories have this state as approximate active state (see section 8.23.1). Multiplet components are summed up. | output.lis | No |
| 4 | Generate a histogram with definable bins (variable width). Bin the trajectories according to their total spin expectation value (of the currently active diagonal state). | output.lis | No |
| 5 | Generate a histogram with definable bins (variable width). Bin the trajectories according to their state dipole moment expectation value (of the currently active diagonal state). | output.lis | No |
| 6 | Generate a histogram with definable bins (variable width). Bin the trajectories according to the oscillator strength between lowest and currently active diagonal states. | output_data/fosc.out | Yes |
| 7 | Calculate the sum of the absolute squares of the diagonal coefficients for each state. | output_data/coeff_diag.out | Yes |
| 8 | Calculate the sum of the absolute squares of the MCH coefficients for each state. | output_data/coeff_MCH.out | Yes |
| 9 | Calculate the sum of the absolute squares of the MCH coefficients for each state. Multiplet components are summed up. | output_data/coeff_MCH.out | Yes |
| 12 | Transform option 1 to MCH basis (section 8.5). | output_data/coeff_class_MCH.out | Yes |
| 13 | Transform option 1 to MCH basis (section 8.5). Multiplet components are summed up. | output_data/coeff_class_MCH.out | Yes |
| 14 | Wigner-transform option 1 to MCH basis (section 8.5). | output_data/coeff_mixed_MCH.out | Yes |
| 15 | Wigner-transform option 1 to MCH basis (section 8.5). Multiplet components are summed up. | output_data/coeff_mixed_MCH.out | Yes |
| 20 | Calculate the sum of the absolute squares of the diabatic coefficients for each state (Only for trajectories with local diabatization). | output_data/coeff_diab.out | Yes |
| 21 | Transform option 1 to diabatic basis (section 8.5). | output_data/coeff_class_diab.out | Yes |
| 22 | Wigner-transform option 1 to diabatic basis (section 8.5). Multiplet components are summed up. | output_data/coeff_mixed_diab.out | Yes |
Run data extractor
For analysis modes 6, 7, 8, 9 and 20 it is necessary to first run the data extractor (see section 7.11). This task can be accomplished by populations.py. However, for a large ensemble or for long trajectories this may take some time. Hence, it is not necessary to perform this step each time populations.py is run.
populations.py will detect whether the file output.dat or the content of output_data/ is more recent. Only if output.dat is newer the data_extractor.x will be run for this trajectory.
Note that mode 20 can only be used for trajectories using local diabatization propagation (keyword coupling overlap in SHARC input file) or .
Number of states
For analysis modes 1, 2, 3, 7, 8 and 9 it is necessary to specify the number of states in each multiplicity. The number is auto-detected from the input file of one of the trajectories.
Intervals
For analysis modes 4, 5 and 6 the user must specify the intervals (i.e., the histogram bins) for the classification of the trajectories. The user has to input a list of interval borders, e.g.:
Please enter the interval limits, all on one line. Interval limits: 1e-3 0.01 0.1 1
Note that scientific notation can be used. Based on this input, for each time step a histogram is created with the number of trajectories in each interval. The histogram bins are:
- x ≤ 10−3
- 10−3 < x ≤ 0.01
- 0.01 < x ≤ 0.1
- 0.1 < x ≤ 1
- 1 < x
Note that there is always one more bin that interval borders entered.
Normalization
If desired, populations.py can normalize the populations by dividing the populations by the number of trajectories.
Maximum simulation time
This gives the maximum simulation time until which the populations are analyzed. For trajectories which are shorter than this value, the last population information is used to make the trajectory long enough. Trajectories which are longer are not analyzed to the end. populations.py prints the length of the shortest and longest trajectories after the analysis.
If diagnostics.py was executed previously, the user can enter here the threshold for the maximum usable time (see section 7.15).
Setup for bootstrapping
The output file of populations.py is sufficient to perform kinetic model fits with the script make_fitscript.py.
However, if error estimates for the kinetic model are desired (using bootstrap.py), the output file of populations.py is not enough.
The user can tell populations.py to save additional data which is required by bootstrap.py.
Gnuplot script
populations.py can generate an appropriate GNUPLOT script for the performed population analysis.
7.16.2 Output
By default, populations.py writes the resulting populations to pop.out. If the file already exists, the user is ask whether it shall be overwritten, or to provide an alternative filename. Note that the output file is checked only after the analysis is completed, so the program might run for a considerable amount of time before asking for the output file.
7.17 Calculation of Numbers of Hops: transition.py
Another important information from the trajectory ensemble is the number of hopping events and the involved states, for example to judge the relative importance of competing reaction pathways.
The interactive script transition.py calculates from an ensemble the number of hops between each pair of states and presents the results as “transition matrices”.
Currently, the script employs the MCH active state information from output.lis for this computations.
Note that since the MCH active state is only an approximate quantity (since hops are actually performed in the diagonal basis in SHARC), the results should be checked carefully.
The script transition.py is still partly work-in-progress.
7.17.1 Usage
The script is interactive, simply start it with no command-line arguments or options:
user@host> $SHARC/transition.py
Paths to trajectories
First the script asks the user to specify all directories for whose content the analysis should be performed. Enter one directory path at a time, and finish the directory input section by typing “end“. Please do not specify each trajectory directory separately, but specify their parent directories, e.g. the directories Singlet_1 and Singlet_2. populations.py will automatically include all trajectories contained in these directories.
If you want to exclude certain trajectories from the analysis, it is sufficient to create an empty file called CRASHED or RUNNING in the corresponding trajectory directory. populations.py will ignore all directories containing one of these files. The file name is case insensitive, i.e., also files like crashed or even cRasHED will lead to the trajectory being ignored.
Additionally, transition.py will ignore trajectories with a DONT_ANALYZE file from diagnostics.py.
Analysis mode
The different analysis modes for transition.py are given in Table 7.10.
| Mode | Description | From which | Extract? |
| file? | |||
| 1 | Get transition matrix in MCH basis. | output.lis | No |
| 2 | Get transition matrix in MCH basis, ignoring hops within multiplets. | output.lis | No |
| 3 | Write a tabular file with the transition matrix in the MCH basis for each time step. | output.lis | No |
| 4 | Write a tabular file with the transition matrix in the MCH basis for each time step, ignoring hops within multiplets. | output.lis | No |
7.18 Fitting population data to kinetic models: make_fit.py
Often it is interesting to fit some functions to the population data from a trajectory ensemble, in order to provide a way to abstract the data and to obtain some kind of rate constants for population transfer, which allows to compare to experimental works.
In simple cases, it might be sufficient to fit basic mono- and biexponential functions to the data, which provides the sought-after time constants.
However, often a more meaningful approach is based on a chemical kinetics model.
Such a model is specified by a set of chemical species (e.g., electronic states, reactants, products, etc) connected by elementary reactions with associated rate constants, which together form a reaction network graph.
For an explanation of those graphs, see section 8.10.
The script make_fit.py helps the user in implementing and fitting such global fits to a kinetics model.
The script works in a stand-alone fashion, unlike its predecessors (make_fitscript.py and bootstrap.py).
It solves the differential equations numerically using a Runge-Kutta 5th order algorithm and fits the kinetic parameters using a number of different optimization algorithms.
The script requires Python2 with NUMPY and SCIPY.
If these are not available, use make_fitscript.py and bootstrap.py.
Often, one is also interested in obtaining an estimate of the error associated to these rate constants, e.g., in order to decide whether enough trajectories were computed.
A possible way to obtain such error estimates is the statistical bootstrapping procedure.
The idea of bootstrapping is to generate resamples of the original ensemble; for an ensemble of n trajectories, one draws n random trajectories with replacement to obtain one resample.
The resample can then be fitted like the original ensemble to obtain a second estimate of the rate constants.
By generating many resamples, one can thus obtain a “probability” distribution of the rate constants, from which a statistical error measure can be calculated.
For details on these statistical measures, see section 8.4.
The script make_fit.py implements this resampling-fitting-statistics procedure.
It is dependent on the output of populations.py, but otherwise works in a stand-alone fashion.
7.18.1 Usage
The script is interactive, simply start it with no command-line arguments or options:
user@host> $SHARC/make_fit.py
Before you start the script, you need to prepare a file with the relevant populations data (usually, the output file of populations.py will suffice).
You also might want to run transition.py first, which can help in developing a suitable kinetic model.
7.18.2 Input
The interactive input for this script consists of specifying the reaction network graph, the initial conditions and the data file.
Additionally, the user has to specify which species should be fitted to which data columns in the file.
Optionally, the user can specify the bootstrap settings for estimating errors.
Kinetic model species
As a first step, the user has to specify the set of species in the model.
Each species is fully described by its label.
A label must start with a letter and can be followed by letters, numbers and underscores (although an underscore must not be directly followed by another underscore).
During input, the user can add one or several labels to the set of species, remove labels and display the current set of defined labels.
It is not possible to add a label twice.
Once all labels are defined, the keyword end brings the user to the next input section (hence, end is not a valid label).
Kinetic model elementary reactions
Next, the reactions have to be defined.
A reaction is specified by its initial species, final species, and reaction rate label.
Reaction rate labels are under the same restrictions as species labels and must not be already used as a species label.
Furthermore, initial and final species must be both defined previously and they must be different.
There can only be one reaction from any species to another species (If a second reaction is defined, the first reaction label is simply overwritten).
Note that reaction rate labels can be used in several reactions (in this way, different rates can be restricted to be the same).
During input, the user can add and remove reactions and display the currently defined reactions (displayed as a matrix).
Unlike species labels, only one reaction can be added per line.
Once all reactions are defined, the keyword end brings the user to the next input section.
Kinetic model initial values
In order to specify the initial values for each species, the user simply has to define which species have non-zero initial population.
These species will then be assigned an initial population constant, which can be fitted along with the reaction rates.
During input, the user can add and remove species from the set of species with non-zero initial population.
Once all reactions are defined, the keyword end brings the user to the next input section.
Operation mode
The script can either read a pop.out file for a simple global fit, or a bootstrap_data/ directory for a global fit with error estimate.
If the latter is chosen, the user needs to enter the number of bootstrap cycles.
Populations data file
The user has to specify a path (autocomplete is enabled) to the file containing the population data to which the model functions should be fitted.
In bootstrap mode, instead the path to the bootstrap_data/ directory (can be prepared with populations.py) needs to be given.
The script reads the file/files and automatically detects the maximum time and the number of data columns.
The file/files should be formatted as a table, with one time step per line (e.g., an output file of populations.py).
On each line, the first number is interpreted as the time in femtoseconds and all consecutive numbers (separated by spaces) as the populations at this time.
Note that the first entry must be at t=0 and all subsequent lines must be in strictly increasing order.
Time steps can be unevenly spaced if necessary.
Species-Data mapping
In the next setup section, the user has to specify which functions should be fitted to which data column from the data file.
In the simplest case, one species is fitted to a single data column (e.g., the species S0 is fitted to data column 2).
However, it is also possible to fit the sum of two species to a column (this can be useful, e.g., to describe biexponential processes) and to fit a species to the sum of several columns (e.g., one can fit to the total triplet population to obtain a total ISC rate constant).
In general, it is also possible to fit sums of species to sums of columns.
It is not allowed to use one species or one column in more than one mapping.
However, it is possible to leave species or data columns unused in the global fit.
While unused species still affect the outcome (through the reaction network definitions), unused data columns are simply ignored in the fit.
During input, the user can add one mapping per line as well as display the current mappings.
For the column definitions, ranges can be given with the tilde symbol, e.g., 5 9 is interpreted as 5 6 7 8 9.
If a typo is made, the user can reset the mappings and repeat only the mapping input without the need to repeat the previous sections.
Once all mappings are defined, the keyword end finishes the input section.
Fitting procedure
In the last section, the user can edit the initial guesses for the rate constants and initial populations.
To change a value, enter label = value.
Use show to print the current values for all constants.
end finishes the guess edit step.
Afterwards, the script asks whether the initial populations should be optimized or not.
This is usually only useful if several species have non-zero initial populations.
If you optimize initial populations, note that their sum might differ from 1 after optimization.
The script also asks whether the rate constants should be constrained to positive values.
If answered with yes, then the optimized rate constants are restricted to the range 0.000 001 to infinity (i.e., the time constants are constrained between 1 000 000 fs and 0 fs).
Note that with constraints SCIPY uses the Trust Region Reflective algorithm, and the Levenberg-Marquardt algorithm for unconstrained cases.
7.18.3 Output
The script will write the output to standard out.
It will first print the iterations of the fit, and the obtained results afterwards (all fitted parameters with errors).
The script will also write two files, fit_results.txt and fit_results.gp.
The latter is a GNUPLOT script that can be used to plot the global fit, which is useful for visual inspection.
Note that the errors printed for normal runs are just the intrinsic fitting errors, which assume that the population data is error-free.
To obtain realistic fitting errors that take into account the uncertainty due to the finite trajectory ensemble, use the bootstrap mode.
In bootstrap mode, the script initially will perform the same steps as in normal mode, using the average population from the bootstrap directory.
After writing the fit results and the two files, the script will start performing the bootstrap iterations, writing the fitted parameters in each iteration.
In this way, the user can monitor the convergence of these values, to decide whether more iterations are required.
Typically, the values and errors will vary strongly during the first iterations and stabilize later.
The convergence rate is strongly dependent on the fitting model and the data.
After all iterations are done (or the script is interrupted with Ctrl-C), the script will print a summary of the statistical analysis.
For each fitting parameter (all time constants and all initial populations), the script will list the arithmetic mean and standard deviation (absolute and relative), the geometric mean and standard deviation (separately for + and −, absolute and relative), and the minimum and maximum values.
The script will also print a histogram with the obtained distribution for each parameter.
For details on these statistical measures, see section 8.4.
bootstrap.py also creates an output file once it is finished.
The file, fit_bootstrap.txt, contains the summary of the statistical analysis with the computed statistical measures and the histograms.
Additionally, at the end this file contains a table with all obtained fitting parameters for resamples (e.g., for further statistical or correlation analysis).
7.19 Fitting population data to kinetic models: make_fitscript.py
This script has been superseded by make_fit.py (see section 7.18).
You should use make_fitscript.py only if make_fit.py does not work.
Often it is interesting to fit some functions to the population data from a trajectory ensemble, in order to provide a way to abstract the data and to obtain some kind of rate constants for population transfer, which allows to compare to experimental works.
In simple cases, it might be sufficient to fit basic mono- and biexponential functions to the data, which provides the sought-after time constants.
However, often a more meaningful approach is based on a chemical kinetics model.
Such a model is specified by a set of chemical species (e.g., electronic states, reactants, products, etc) connected by elementary reactions with associated rate constants, which together form a reaction network graph.
For an explanation of those graphs, see section 8.10.
The script make_fitscript.py helps the user in implementing and executing such global fits to a kinetics model.
The script employs the open-source computer algebra system MAXIMA as back-end to solve the differential equation systems which describe the model kinetics.
The script writes a GNUPLOT script containing all commands necessary for the global fit.
The fitting itself is performed with GNUPLOT.
7.19.1 Usage
The script is interactive, simply start it with no command-line arguments or options:
user@host> $SHARC/make_fitscript.py
Before you start the script, you need to prepare a file with the relevant populations data (usually, the output file of populations.py will suffice).
You also might want to run transition.py first, which can help in developing a suitable kinetic model.
7.19.2 Input
The interactive input for this script consists of specifying the reaction network graph, the initial conditions and the data file.
Additionally, the user has to specify which species should be fitted to which data columns in the file.
Kinetic model species
As a first step, the user has to specify the set of species in the model.
Each species is fully described by its label.
A label must start with a letter and can be followed by letters, numbers and underscores (although an underscore must not be directly followed by another underscore).
During input, the user can add one or several labels to the set of species, remove labels and display the current set of defined labels.
It is not possible to add a label twice.
Once all labels are defined, the keyword end brings the user to the next input section (hence, end is not a valid label).
Kinetic model elementary reactions
Next, the reactions have to be defined.
A reaction is specified by its initial species, final species, and reaction rate label.
Reaction rate labels are under the same restrictions as species labels and must not be already used as a species label.
Furthermore, initial and final species must be both defined previously and they must be different.
There can only be one reaction from any species to another species (If a second reaction is defined, the first reaction label is simply overwritten).
During input, the user can add and remove reactions and display the currently defined reactions (displayed as a matrix).
Unlike species labels, only one reaction can be added per line.
Once all reactions are defined, the keyword end brings the user to the next input section.
Kinetic model initial values
In order to specify the initial values for each species, the user simply has to define which species have non-zero initial population.
These species will then be assigned an initial population constant (e.g., for species A the initial population constant would be A__0).
These constants will show up in the GNUPLOT script and their value can edited there.
It is also possible to fit the initial populations to the data.
During input, the user can add and remove species from the set of species with non-zero initial population.
Once all reactions are defined, the keyword end brings the user to the next input section.
Populations data file
The user has to specify a path (autocomplete is enabled) to the file containing the population data to which the model functions should be fitted.
The script reads the file and automatically detects the maximum time and the number of data columns.
The file should be formatted as a table, with one time step per line (e.g., an output file of populations.py).
On each line, the first number is interpreted as the time in femtoseconds and all consecutive numbers (separated by spaces) as the populations at this time.
Note that the first entry must be at t=0 and all subsequent lines must be in strictly increasing order.
Time steps can be unevenly spaced if necessary.
Species-Data mapping
In the final setup section, the user has to specify which functions should be fitted to which data column from the data file.
In the simplest case, one species is fitted to a single data column (e.g., the species S0 is fitted to data column 2).
However, it is also possible to fit the sum of two species to a column (this can be useful, e.g., to describe biexponential processes) and to fit a species to the sum of several columns (e.g., one can fit to the total triplet population to obtain a total ISC rate constant).
In general, it is also possible to fit sums of species to sums of columns.
It is not allowed to use one species or one column in more than one mapping.
However, it is possible to leave species or data columns unused in the global fit.
While unused species still affect the outcome (through the reaction network definitions), unused data columns are simply ignored in the fit.
During input, the user can add one mapping per line as well as display the current mappings.
If a typo is made, the user can reset the mappings and repeat only the mapping input without the need to repeat the previous input.
Once all mappings are defined, the keyword end finishes the input section.
Running MAXIMA
Before the script attempts to call MAXIMA, it prints the command to be executed and asks the user for permission to execute.
If permission is denied, the user may enter another command to call maxima.
After permission is granted, the script calls MAXIMA.
If the call takes more than a few seconds, the standard output of MAXIMA is printed and standard input is switched to MAXIMA.
In this way, the user can answer any questions by MAXIMA (e.g., whether a constant/combination of constants is larger than zero).
To answer these questions, type the answer followed by a semi-colon (e.g., pos;).
7.19.3 Output
After successful execution of the script, two files are created, model_fit.dat and model_fit.gp.
The former file contains the populations data formatted appropriately for the global fit.
The latter file contains the GNUPLOT script which can be executed by
user@host> gnuplot model_fit.gp
to perform the global fit.
Please follow the instructions printed by make_fitscript.py at the end of the execution, in particular by adjusting the starting guesses for the fitting parameters (you have to open and edit model_fit.gp for this).
Please do not change the structure of model_fit.gp if you intend to use this file with bootstrap.py.
7.20 Estimating Errors of Fits: bootstrap.py
This script has been superseded by make_fit.py (see section 7.18).
You should use bootstrap.py only if make_fit.py does not work.
As was described in section 7.19, the population data from populations.py can be fitted to a kinetic model to obtain interpretable rate constants.
Often, one is also interested in obtaining an estimate of the error associated to these rate constants, e.g., in order to decide whether enough trajectories were computed.
A possible way to obtain such error estimates is the statistical bootstrapping procedure.
The idea of bootstrapping is to generate resamples of the original ensemble; for an ensemble of n trajectories, one draws n random trajectories with replacement to obtain one resample.
The resample can then be fitted like the original ensemble to obtain a second estimate of the rate constants.
By generating many resamples, one can thus obtain a “probability” distribution of the rate constants, from which a statistical error measure can be calculated.
For details on these statistical measures, see section 8.4.
The script bootstrap.py implements this resampling-fitting-statistics procedure.
It is dependent on the output of populations.py and make_fitscript.py, and employs GNUPLOT to perform the actual fits.
7.20.1 Usage
The script is interactive, simply start it with no command-line arguments or options:
user@host> $SHARC/bootstrap.py
Before you start the script, you need to run populations.py to generate the bootstrapping data (populations.py asks the related question near the end of the input query).
Additionally, you need to use make_fitscript.py to generate a GNUPLOT fitting script. Please, do not modify the script (beyond initial values for the fitting constants), as bootstrap.py relies on the proper format of this file.
It is advisable to create the GNUPLOT fitting script from one of the files contained in the bootstrap data directory (because then the simulation time is consistent between the fitting script and the bootstrapping data).
7.20.2 Input
The interactive input consists in specifying the paths to the bootstrapping data directory (from populations.py), the path to the fitting script, the number of resamples, and some other minor options.
Path to the bootstrapping data directory
The user should enter here the path to the directory which was created by populations.py and which contains the bootstrapping raw data (i.e., the populations for each individual trajectory before summing up over the ensemble).
bootstrap.py automatically detects the number of trajectories, time step, number of steps, and number of data columns.
Note that bootstrap.py only considers files in this directory if their filename starts with pop_.
Also note that bootstrap.py creates a temporary subdirectory inside the bootstrapping data directory as scratch area.
Number of bootstrapping cycles
Here, the number of resamples to generate and fit needs to be entered.
The default, 10 resamples, is very small and not sufficient to achieve convergence in the errors for most applications.
It is advisable to employ several hundred or thousand resamples to achieve good statistical convergence.
Note that the script can be interrupted during the iterations (using Ctrl-C) and then skips to the final analysis, so it is no problem to enter a too large number of cycles.
Random number generator seed
The script employs random numbers to generate the random resamples.
For reproducible results, do not use the default option (!), but enter an integer.
Path to the fitting script
The user should enter the path to the appropriate GNUPLOT fitting script, generated with make_fitscript.py.
It is strongly advisable to adjust the initial guesses for the fitting parameters in the script in order to ensure quick and stable convergence of the fits.
Please, do not modify the generated GNUPLOT script in any other way, as this might break bootstrap.py.
Command to execute
Here, the user should enter the command to be used to call GNUPLOT. In most cases, this will simply be gnuplot, but the user might want to use another installation of GNUPLOT for the fitting.
Number of CPUs
bootstrap.py can be run in parallel mode, where multiple GNUPLOT processes are employed at the same time.
Currently, this parallelization is not very efficient due to process creation overheads, but for complicated fitting scripts (where each fit takes relatively long), large data sets, or many resamples it can be useful.
Note that if more than one CPU is used, users should not prematurely terminate bootstrap.py with Ctrl-C, as some of the subprocesses might get stuck and the script will not properly go to the final analysis.
7.20.3 Output
During the resample iterations, bootstrap.py prints the current values and errors (geometric mean and geometric standard deviation) of the fitting parameters every few iterations.
In this way, the user can monitor the convergence of these values, to decide whether more iterations are required.
Typically, the values and errors will vary strongly during the first iterations and stabilize later.
The convergence rate is strongly dependent on the fitting model and the data.
After all iterations are done (or the script is interrupted with Ctrl-C), the script will print a summary of the statistical analysis.
For each fitting parameter (all time constants and all initial populations), the script will list the arithmetic mean and standard deviation (absolute and relative), the geometric mean and standard deviation (separately for + and −, absolute and relative), and the minimum and maximum values.
The script will also print a histogram with the obtained distribution for each parameter.
For details on these statistical measures, see section 8.4.
bootstrap.py also creates two output files.
The first file, bootstrap_cycles.out, is written on-the-fly while the resample iterations are running.
It contains the same tabular output as is shown in standard output, and can be used to visualize the convergence behavior of the parameters. For example, the first parameter can be monitored using GNUPLOT with this command: plot "bootstrap_cycles.out" using 1:6:8 w yerrorbars.
The scond file, bootstrap.out, is written once the final analysis is complete. It contains the summary of the statistical analysis with the computed statistical measures and the histograms.
Additionally, at the end this file contains a table with all obtained fitting parameters for resamples (e.g., for further statistical or correlation analysis).
7.21 Obtaining Special Geometries: crossing.py
In many cases, it is also important to obtain certain special geometries from the trajectories. The script crossing.py extracts geometries fulfilling special conditions from an ensemble of trajectories.
Currently, crossing.py finds geometries where the approximate MCH state (see section 8.23.1) of the last time step is different from the MCH state of the current time step (i.e. crossing.py finds geometries where surface hops occured).
7.21.1 Usage
The script is interactive, simply start it with no command-line arguments or options:
user@host> $SHARC/crossing.py
The input to the script is very similar to the one of populations.py.
Paths to trajectories
First the script asks the user to specify all directories for whose content the analysis should be performed. Enter one directory path at a time, and finish the directory input section by typing “end“. Please do not specify each trajectory directory separately, but specify their parent directories, e.g. the directories Singlet_1 and Singlet_2. crossing.py will automatically include all trajectories contained in these directories.
If you want to exclude certain trajectories from the analysis, it is sufficient to create an empty file called CRASHED or RUNNING in the corresponding trajectory directory. crossing.py will ignore all directories containing one of these files.
Additionally, crossing.py will ignore trajectories with a DONT_ANALYZE file from diagnostics.py.
Analysis mode
Currently, crossing.py only supports one analysis mode, where crossing.py is scanning for each trajectory the file output.lis. If the occupied MCH state (column 4 in output file output.lis) changes from one time step to the next, it is checked whether the old and new MCH states are the ones specified by the user. If this is the case, the geometry corresponding to the new time step (t) is retrieved from output.xyz (lines t(natom+2)+1 to t(natom+2)+natom).
States involved in surface hop
First, the user has to specify the permissible old MCH state. The state has to be specified with two integers, the first giving the multiplicity (1=singlet, …), the second the state within the multiplicity (1 1=S0, 1 2=S1, etc.). If a state of higher multiplicity is given, crossing.py will report all geometries where the old MCH state is any of the multiplet components.
For the new MCH state, the same is valid.
Third, the direction of the surface hop has to be specified. Choosing “Backwards” has the same effect as exchanging the old and new MCH states.
7.21.2 Output
All geometries are in the end written to an output file, by default crossing.xyz. The file is in standard xyz format. The comment of each geometry gives the path to the trajectory where this geometry was extracted, the simulation time and the diagonal and MCH states at this simulation time.
7.22 Internal Coordinates Analysis: geo.py
SHARC writes at every time step the molecular geometry to the file output.xyz. The non-interactive script geo.py can be used in order to extract internal coordinates from xyz files. The usage is:
user@host> $SHARC/geo.py [options] < Geo.inp > Geo.out
By default, the coordinates are read from output.xyz, but this can be changed with the -g option (see table 7.12). Note that the internal coordinate specifications are read from standard input and the result table is written to standard out.
7.22.1 Input
The specifications for the desired internal coordinates are read from standard input. It follows a simple syntax, where each internal coordinate is specified by a single line of input. Each line starts with a one-letter key which specifies the type of internal coordinate (e.g. bond length, angle, dihedral, …). The key is followed by a list of integers, specifying which atoms should be measured. As a simple example, r 1 2 specifies the bond length (r is the key for bond lengths) between atoms 1 and 2. Note that the numbering of the atoms starts with 1. Each line of input is checked for consistency (whether any atom index is larger than the number of atoms, repeated atom indices, misspelled keys, wrong number of atom indices, …), and erroneous lines are ignored (this is indicate by an error message).
Table 7.11 lists the available types of internal coordinates. The output is a table, where the first column is the time (Actually, the geometries are just enumerated starting with zero, and the number multiplied by the time step from the -t option). The successive columns in the output table list the results of the internal coordinates calculations. Each request generates at least one column, see table 7.11.
Note that for most internal coordinates, the order of the atoms is crucial, since e.g. a123 ≠ a213. This also holds for the Cremer-Pople parameter requests. For these input lines, the atoms should be listed in the order they appear in the ring (clockwise or counter-clockwise).
| Key | Atom | Description | Output columns |
| Indices | |||
| x | a | x coordinate of atom a | x |
| y | a | y coordinate of atom a | y |
| z | a | z coordinate of atom a | z |
| r | a b | Bond length between a and b | r |
| a | a b c | Angle between a–b and b–c | a |
| d | a b c d | Dihedral, i.e., angle between normal vectors of (a,b,c) and (b,c,d) | d |
| (between -180° and 180°, same sign conventions as MOLDEN) | |||
| p | a b c d | Pyramidalization angle: 90° minus angle between bond a–b | p |
| and normal vector of (b,c,d) | |||
| q | a b c d | Pyramidalization angle (alternative definition; angle between | q |
| bond a–b and average of bonds b–c and b–d | |||
| 5 | a b c d e | Cremer-Pople parameters for 5-membered rings [79] and | q2, ϕ2, Boeyens |
| comformation classification. | |||
| 6 | a b c d e f | Cremer-Pople parameters for 6-membered rings [79] and | Q, ϕ, θ, Boeyens |
| Boeyens classification [80]. | |||
| i | a – f | Angle between average plane through 3-rings (a - c) and (d - f) | i |
| j | a – h | Angle between average plane through 4-rings (a - d) and (e - f) | j |
| k | a – j | Angle between average plane through 5-rings (a - e) and (f - j) | k |
| l | a – l | Angle between average plane through 6-rings (a - f) and (g - l) | l |
| c | Writes the comment (second line of the | Comment | |
| xyz format) to the table. |
As an advice, it is always a good idea to put the comment as the last request, if needed. Since the comment may contain blanks, having the comment not as the very last column might make it impossible to plot the resulting table.
The Boeyens classification symbols which are output for 6-membered rings are reported in LATEX math code. Note that in the Boeyens classification scheme by definition a number of symbols are equivalent, and only one symbol is reported.
These are the equivalent symbols: 1C4=3C6=5C2, 4C1=6C3=2C5, 1T3=4T6, 2T6=5T3, 2T4=5T1, 3T1=6T4, 6T2=3T5 and 4T2=1T5.
For 5-membered rings, the classification symbols are chosen similar to the Boeyens symbols. For the aE and Ea symbols, atom a is puckered out of the plane and the four other atoms are coplanar, while for the aHb symbols the neighboring atoms a and b are puckered out of the plane in opposite directions and only the three remaining atoms are coplanar.
It is also possible to measure angles between the average planes through two n-membered rings.
Currently, this is only possible if both rings have the same number of atoms (3, 4, 5, or 6).
7.22.2 Options
geo.py accepts a number of command-line options, see table 7.12. All options have sensible defaults. However, especially if long comments should be written to the output file, it might be necessary to increase the field width. Note that the minimum column width is 20 so that the table header can be printed correctly.
Also note that the column for the comment is enlarged by 50 characters.
| Option | Description | Default |
| -h | Display help message and quit. | – |
| -b | Report x, y, z, r, q2 and Q in Bohrs | Angstrom |
| -r | Report a, d, p, q, ϕ2, ϕ, θ, i, j, k, and l in Radians | Degrees |
| -g FILENAME | Read coordinates from the specified file | output.xyz |
| -t FLOAT | Assumed time step between successive geometries (fs) | 1.0 fs |
| -T INTEGER | Start counting time step | 0 |
| -w INTEGER | Width of each column (min=20) | 20 |
| -p INTEGER | Precision (Number of decimals, min=width-3) | 4 |
7.23 Essential Dynamics Analysis: trajana_essdyn.py
An essential dynamics analysis [83] is a procedure to find the most active vibrational modes in an ensemble of trajectories.
It is based on the computation of the covariance matrix between all Cartesian (or mass-weighted Cartesian) coordinates of all steps of all trajectories and a singular value decomposition of this covariance matrix.
For details on the computation, see section 8.8.
The interactive script trajana_essdyn.py can be used to perform such an analysis.
7.23.1 Usage
trajana_essdyn.py is an interactive script, which is started with:
user@host> $SHARC/trajana_essdyn.py
Note that before executing the script you should prepare an XYZ geometry file with the reference geometry (e.g., the ground state minimum or the average geometry from the trajectories).
7.23.2 Input
During interactive input, the script queries for the paths to the trajectories, the path to the reference structure, and a few other settings.
Path to the trajectories
First the script asks the user to specify all directories for whose content the analysis should be performed. Enter one directory path at a time, and finish the directory input section by typing “end“. Please do not specify each trajectory directory separately, but specify their parent directories, e.g. the directories Singlet_1 and Singlet_2. trajana_essdyn.py will automatically include all trajectories contained in these directories.
If you want to exclude certain trajectories from the analysis, it is sufficient to create an empty file called CRASHED or RUNNING in the corresponding trajectory directory. trajana_essdyn.py will ignore all directories containing one of these files.
Additionally, trajana_essdyn.py will ignore trajectories with a DONT_ANALYZE file from diagnostics.py.
Path to reference structure
For the essential dynamics analysis, a reference structure is required. This structure is substracted from all geometries for the correlation analysis.
The structure can be in any format understandable by OPENBABEL, but the type of format needs to be specified.
In most cases, the reference structure will be either in XYZ or MOLDEN format.
Mass-weighted coordinates
If enabled, the correlation analysis will be carried out in mass-weighted Cartesian coordinates.
In the output file, the mass-weighting will be removed properly.
Number of steps and time step
These parameters are automatically detected and suggested as defaults.
It is not necessary to change them.
Time step intervals
By default, trajana_essdyn.py will analyze the full length of the simulations together.
However, it is also possible to compute the essential dynamics for different time intervals (e.g., if the molecular motion is different in the beginning of the dynamics).
Multiple, possibly overlapping, intervals can be entered; for each of the intervals, one set of output files is produced.
Results directory
The path to the directory where the output files are stored.
The path has to be entered as a relative or absolute path.
If it does not exist, trajana_essdyn.py will create it.
7.23.3 Output
Inside the results directory, trajana_essdyn.py will create two subdirectories, total_cov/ and cross_av/.
In the directory total_cov/ the results of the full covariance analysis are stored (i.e., essential modes found here have large total activity, but the trajectories could behave very differently).
On the contrary, cross_av/ will contain the results of the analysis of the average trajectory (i.e., essential modes found here have strongly coherent activity, where all trajectories behave similarly).
For each time step interval entered, one output file (e.g., 0-1000.molden) is created in each of the two subdirectories.
7.24 Normal Mode Analysis: trajana_nma.py
A normal mode analysis [81] is a procedure to find the activity of given normal modes in an ensemble of trajectories
For details on the computation, see section 8.19.
The interactive script trajana_nma.py can be used to perform such an analysis.
7.24.1 Usage
trajana_nma.py is an interactive script, which is started with:
user@host> $SHARC/trajana_nma.py
Note that before executing the script you should prepare a MOLDEN file with the relevant normal modes.
7.24.2 Input
During interactive input, the script queries for the paths to the trajectories, the path to the normal mode file, and a few other settings.
Path to the trajectories
First the script asks the user to specify all directories for whose content the analysis should be performed. Enter one directory path at a time, and finish the directory input section by typing “end“. Please do not specify each trajectory directory separately, but specify their parent directories, e.g. the directories Singlet_1 and Singlet_2. trajana_nma.py will automatically include all trajectories contained in these directories.
If you want to exclude certain trajectories from the analysis, it is sufficient to create an empty file called CRASHED or RUNNING in the corresponding trajectory directory. trajana_nma.py will ignore all directories containing one of these files.
Additionally, trajana_nma.py will ignore trajectories with a DONT_ANALYZE file from diagnostics.py.
Path to normal mode file
The normal mode file (in MOLDEN format) needs to contain the normal modes for which the analysis should be carried out.
The file needs to have the same atom ordering as the trajectories.
Mass-weighted coordinates
If enabled, the correlation analysis will be carried out in mass-weighted Cartesian coordinates.
In the output file, the mass-weighting will be removed properly.
Number of steps and time step
These parameters are automatically detected and suggested as defaults.
It is not necessary to change them.
Automatic plot creation
If available, the user can choose to automatically create total activity and temporal plots of the normal mode analysis.
Non-totally symmetric modes
For symmetry reasons, the average value of a non-totally symmetric normal mode will always be close to zero for a sufficiently large ensemble.
In order to still obtain useful information for such modes, the user can specify modes whose absolute value should be considered.
Note that in the input it is possible to specify ranges, e.g., 28 for all modes from 2 to 8.
Multiplication by -1
The user can choose to multiply certain normal modes by -1.
This is only for convenience when viewing the results.
Note that in the input it is possible to specify ranges, e.g., 28 for all modes from 2 to 8.
Time step intervals
By default, trajana_nma.py will analyze the full length of the simulations together.
However, it is also possible to compute the essential dynamics for different time intervals (e.g., if the molecular motion is different in the beginning of the dynamics).
Multiple, possibly overlapping, intervals can be entered; for each of the intervals, one set of output files is produced.
Results directory
The path to the directory where the output files are stored.
The path has to be entered as a relative or absolute path.
If it does not exist, trajana_nma.py will create it.
7.24.3 Output
Inside the results directory, trajana_nma.py will create one subdirectory, nma/.
By default, four output files are written into this subdirectory.
The file total_std.txt will contain the mode activity for each normal mode and for each time interval; a large value indicates that across all time steps and trajectories there is a large variance in that normal mode.
Similarly, the file cross_av_std.txt will contain the mode activity for each normal mode and for each time interval; this is computed from the average trajectory, therefore only showing coherent mode activity.
The files mean_against_time.txt and std_against_time.txt contain for all normal modes and for all time steps the mean and standard deviation, respectively.
Also by default, additionally, inside each of the trajectory directories, trajana_nma.py generates three output files.
The file nma_nma.txt is a table containing the normal mode coordinates of the trajectory for each time step; functionally, it is very similar to the output of geo.py.
The files nma_nma_av.txt and nma_nma_std.txt contain for each time interval and each normal mode the mean and average for that trajectory.
Finally, if automatic plots were requested, the results subdirectory will contain two directories, bar_graphs/ and time_plots/.
The former contains plots of the data in total_std.txt and cross_av_std.txt, whereas the latter will contain plots of mean_against_time.txt and std_against_time.txt.
7.25 General Data Analysis: data_collector.py
Whereas most of the other analysis scripts in the SHARC suite are intended for rather specific tasks, data_collector.py is aimed at providing a general analysis tool to carry out a large variety of tasks.
The primary task of data_collector.py is to collect tabular data from files which are present in all trajectories, possibly perform some analysis procedures (smoothing, averaging, convoluting, integrating, summing), and output the combined data as a single file.
Possible applications of this functionality are statistical analysis of internal coordinates (e.g., mean and variation in a bond length), the creation of hair figures (e.g., a specific bond length plotted for all trajectories), data convolutions (e.g., distribution of bond length over time, simulation of time- and energy-resolved spectra), or data integration (e.g., computation of time-resolved intensities).
7.25.1 Usage
data_collector.py is an interactive script, which is started with:
user@host> $SHARC/data_collector.py
7.25.2 Input
In general, the first step in data_collector.py is to collect tabular data files which exist in the directories of multiple trajectories.
For each trajectory, this file needs to have the same file name and the same tabular format; for example, one could read for all trajectories the output.lis files.
Collecting
Hence, in the first input section, the script asks the user to specify all directories for whose content the analysis should be performed. Enter one directory path at a time, and finish the directory input section by typing “end“. Please do not specify each trajectory directory separately, but specify their parent directories, e.g. the directories Singlet_1 and Singlet_2. data_collector.py will automatically include all trajectories contained in these directories.
If you want to exclude certain trajectories from the analysis, it is sufficient to create an empty file called CRASHED or RUNNING in the corresponding trajectory directory. data_collector.py will ignore all directories containing one of these files.
Additionally, data_collector.py will ignore trajectories with a DONT_ANALYZE file from diagnostics.py.
In the second step, data_collector.py displays all files which appear in multiple trajectories and which might be suitable for analysis (the script ignores files which it knows to be not suitable, e.g., output.dat, output.xyz, most files in the QM/ or restart/ subdirectories, …).
All other files (e.g., output.lis, files in output_data/, …) will be displayed, together with the number of appearances.
Once one of the files has been selected, one needs to assign the different data columns.
(i) One column is designated the time column T, which defines the sequentiality of the data:
(ii) Multiple columns can then be designated as data columns, called X columns in the following.
(iii) The same number of columns is designated as weight columns, called Y columns here (weights can be set equal to 1 by selecting column “0” in the relevant menu).
For example, for a time-resolved spectrum, the transition energies would be the X data, whereas the oscillator strengths would be the Y data (weights).
With these assignments, the full data set is defined:
- For each trajectory a
- For each time step t
- For each X column i there will be a value pair (xai(t),yai(t)) or (xai(t),1).
- For each time step t
In the simplest case, there will be exactly one (xa(t),1) pair for each trajectory and time, which is a two-dimensional data set.
Keep in mind that in general, each trajectory could have different time steps at this point.
We refer to this kind of data set (independent trajectories with possibly different time axes) as Type1 data set.
As will be described below, in data_collector.py, during certain processing steps the format of the data set is changed, which will create Type2 or Type3 data sets.
Once this data set is collected from the files (where too short or commented lines are ignored), data_collector.py allows for a number of subsequent processing steps, which are summarized in Figure 7.4.
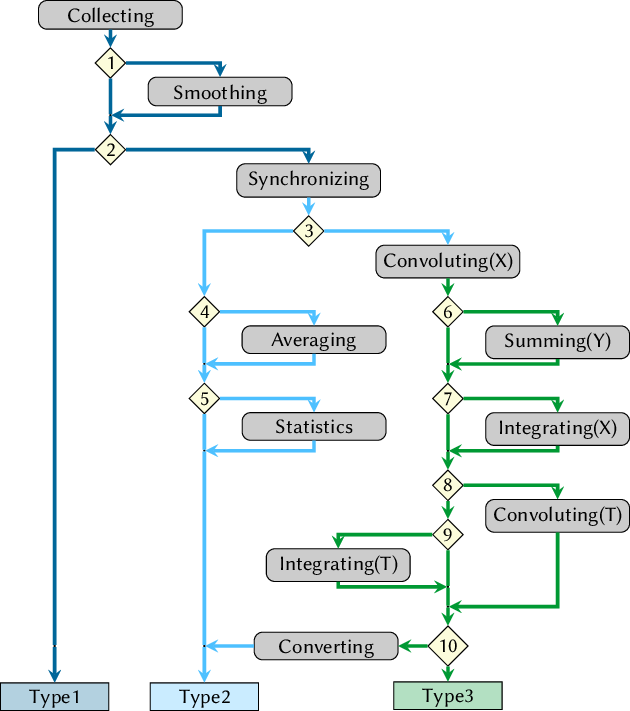
Possible workflows in data_collector.py.
Grey boxes denote the different computational actions, yellow diamonds denote the different decisions which are queried in the input dialog, and the boxes at the denote the three different data set types (dark blue=Type1, light blue=Type2, green=Type3).
The different actions and data set types are explained in the text.
Smoothing
In this step, each trajectory is individually smoothed, using one of several smoothing kernels (Gaussian, Lorentzian, Log-normal, rectangular).
Smoothing does not change the size or format of the data set, each value is simply replaced by the corresponding smoothed value; hence, a new Type1 data set is obtained.
Smoothing is applied to each X and each Y column independently, but always with the same kernel.
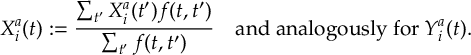 |
(7.1) |
Here, f(t,t′) is the smoothing kernel.
Synchronizing
In this step, the Type1 data set is reformatted, by merging all trajectories together.
This step creates a Type2 data set, which has a common T axis for all trajectories (simply the union of the T columns from all trajectories).
For each time step, all X and Y values of all trajectories are collected.
If a trajectories does not have data at a particular time step, NaNs will be inserted.
In this way, a rectangular, two-dimensional data set is obtained, with as many rows as time steps, and 2ntrajnX data columns.
A simple application of Collecting+Synchronizing could be to generate a table with the bond length for all time steps for all trajectories, in order to generate a “hair figure”.
This task could in principle also be accomplished with Bash tools like awk and paste, but this is troublesome if the trajectories are of different length, with different time steps, or if the table files contain comments.
Averaging
The Type2 data set from the Synchronizing step can contain a large number of data columns (2ntrajnX).
In order to reduce this amount of information, the Averaging step can be used to compute the mean and standard deviation across all trajectories, separately for each time step.
This will create a new Type2 data set, which still has a common time axis, but will only contain 4nX+1 data columns; these are the mean and standard deviation of all X and Y columns, plus one column giving the number of trajectories for each time step.
Currently, this step can be performed with either arithmetic mean/standard deviation or geometric mean/standard deviation.
Statistics
Similar to the Averaging step, the Statistics step computes mean and standard deviations from a Type2 data set.
The difference is that during Statistics, these values are computed for all values from the first to the current time step.
The data in the last time step thus gives the total statistics over all time steps and trajectories.
The Type2 data set from the Statistics step contains the same number of data columns as the one from the Averaging step.
Currently, this step can be performed with either arithmetic mean/standard deviation or geometric mean/standard deviation.
With the Averaging and Statistics steps, it is possible to compute the same data as with trajana_nma.py (if the appropriate files are read), namely the total (Statistics) and coherent (Averaging+Statistics) activity of the normal modes.
Using data_collector.py, the same analysis can also be applied to internal coordinates computed with geo.py.
Convoluting(X)
In order to create a data set which has common T and X axes (a Type3 data set), it is in general necessary to perform some kind of data convolution involving the X column data.
In order to do this, data_collector.py creates a grid along the X axis (ngrid points from the minimum value to the maximum value of all X data in the data set, plus some padding).
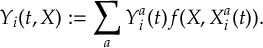 |
(7.2) |
The created Type3 data set has nX data points for each time step and each X grid point.
Using energies as X columns and oscillator strengths/intensities as Y columns, in this way it is possible to compute time-dependent spectra.
Summing(Y)
When nX is larger than one, the Summing step can be used to compute the sum over all data points for each time step and each X grid point.
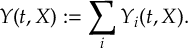 |
(7.3) |
This creates a new Type3 data set, which will only contain one data point for each time step and each X grid point.
For example, for a transient spectrum involving multiple final states (nX > 1), after the Convoluting(X) step one obtains one transient spectrum for each final state. With the Summing(Y) step, one can then compute the total transient absorption spectrum.
Integrating(X)
When computing transient spectra, one is often interested in integrating the spectrum within a certain energy window.
This can be done with the Integrating(X) step.
After entering a lower and upper X limit, a new Type3 data set is created, with only three data points per time step.
The first data point contains the integral from minus infinity to the lower limit, the second data point the integral between lower and upper limit, and the third data point the integral from the upper limit to infinity.
If Summing(Y) was not carried out, this integration is carried out independently for each of the nX data columns.
Convoluting(T)
The Type3 data set can also be convoluted along the time axis (e.g., in order to apply an instrument response function to a time-resolved spectrum).
In order to do this, a uniform grid along the T axis is generated (with nTgrid points from the minimum value to the maximum value of the previous T axis, plus some padding).
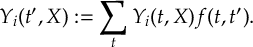 |
(7.4) |
The created Type3 data set has as many data points for each X grid point as before, but the number of time steps is now nTgrid.
Convoluting(T) can be applied also if Summing(Y) and/or Integrating(X) were used (in this case, the kernel is applied to the summed up or integrated data).
Integrating(T)
This step carries out a cumulative summation along the T axis.
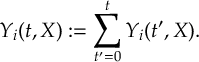 |
(7.5) |
In this way, the data in the last time step constitute the integral over all time steps.
Since all the partial cumulative sums are also computed, integrals within some bounds can simply be computed as differences between partial cumulative sums.
Converting
At the end of the workflow, a Type3 data set can be converted back into a Type2 data set, which affects how the output file is formatted.
This is usually a good idea if the Integrating(X) step was performed, but might not be a good idea otherwise.
See below for how the different data set types are formatted on output.
7.25.3 Output
After the input dialog is finished, data_collector.py will start carrying out the requested analyses.
For each of the workflow steps, one output file is written, so that all intermediate results can be used as well.
Output files have automatically generated filenames, which describe how the data was obtained.
Filenames are always in the form collected_data_<T>_<X>_<Y>_<steps>.<type>.txt, where <T> is an integer giving the T column index, <X> and <y> are lists of integers of the X and Y column indices, <steps> is a string denoting which workflow steps were carried out, and <type> denotes the data set type.
For example, an output file could be named collected_data_1_2_0_sy_cX.type3.txt, where column 1 was the T column, column 2 the X column, no Y column was used, Synchronizing and Convoluting(X) were performed, resulting in a Type3 data set.
Format of Type1 data set output
Type1 data sets are formatted such that each trajectory is given as a continuous block, separated by an empty line.
Within each block, each line contains the data of one time step, order increasingly.
Each line contains a trajectory index, the relative file path, the time, all X column data, and then all Y column data.
# 1 2 3 4 5 6 7 #Index Filename Time X Column 5 X Column 6 Y Column 0 Y Column 0 0 Singlet_1//TRAJ_00001/./Geo.out 0.00000000E+00 1.13340000E-01 7.99096900E+00 1.00000000E+00 1.00000000E+00 0 Singlet_1//TRAJ_00001/./Geo.out 5.00000000E-01 1.59173000E-01 7.94395200E+00 1.00000000E+00 1.00000000E+00 0 Singlet_1//TRAJ_00001/./Geo.out 1.00000000E+00 2.10868000E-01 7.89084000E+00 1.00000000E+00 1.00000000E+00 ... 1 Singlet_1//TRAJ_00002/./Geo.out 0.00000000E+00 5.03990000E-02 7.99078100E+00 1.00000000E+00 1.00000000E+00 1 Singlet_1//TRAJ_00002/./Geo.out 1.00000000E+00 3.80370000E-02 8.00349700E+00 1.00000000E+00 1.00000000E+00 1 Singlet_1//TRAJ_00002/./Geo.out 2.00000000E+00 1.09515000E-01 7.93073500E+00 1.00000000E+00 1.00000000E+00 ... 2 Singlet_1//TRAJ_00004/./Geo.out 0.00000000E+00 2.10908000E-01 8.29417600E+00 1.00000000E+00 1.00000000E+00 2 Singlet_1//TRAJ_00004/./Geo.out 5.00000000E-01 1.49506000E-01 8.35651800E+00 1.00000000E+00 1.00000000E+00 2 Singlet_1//TRAJ_00004/./Geo.out 1.00000000E+00 1.05887000E-01 8.40056700E+00 1.00000000E+00 1.00000000E+00 ...
Note here in the example that the second trajectory has a time step of 1.0 fs and thus no data at 0.5 fs.
Format of Type2 data set output
Type2 data sets are formatted such that all trajectories share a common time axis, hence for each time step there will be one line of data.
Each line starts with the time, followed columns with the data for the first trajectory, followed by the data for the second trajectory, etc.
Within each trajectory, first all X columns, then all Y columns are given. If a Y column contains only unit weights (using special file column “0”), then this Y column is omitted from the Type2 formatted output.
# 1 2 3 4 5 6 7 ... # Time X Column 5 X Column 6 X Column 5 X Column 6 X Column 5 X Column 6 ... 0.00000000E+00 1.13340000E-01 7.99096900E+00 5.03990000E-02 7.99078100E+00 2.10908000E-01 8.29417600E+00 ... 5.00000000E-01 1.59173000E-01 7.94395200E+00 NaN NaN 1.49506000E-01 8.35651800E+00 ... 1.00000000E+00 2.10868000E-01 7.89084000E+00 3.80370000E-02 8.00349700E+00 1.05887000E-01 8.40056700E+00 ... ...
Note here in the example that the second trajectory does not have data at 0.5 fs.
Format of Typ3 data set output
Type3 data sets are formatted such that all trajectories share common time and X axes.
The data is formatted block-wise, with the first block corresponding to the first time step and containing all points on the X grid, followed by an empty line, followed by the second block, etc.
Each block consists of ngrid lines, each starting with the time and X value in the first two columns and followed by nX columns with the convoluted data.
# 1 2 3 4 # Time X_axis Conv(5,0) Conv(6,0) 0.00000000E+00 -1.45534000E-01 2.38544715E-05 0.00000000E+00 0.00000000E+00 2.30671958E-01 1.51462322E+00 0.00000000E+00 0.00000000E+00 6.06877917E-01 1.07930050E-01 0.00000000E+00 ... 5.00000000E-01 -1.45534000E-01 1.31312692E-04 0.00000000E+00 5.00000000E-01 2.30671958E-01 1.28614756E+00 0.00000000E+00 5.00000000E-01 6.06877917E-01 4.46251462E-10 0.00000000E+00 ... 1.00000000E+00 -1.45534000E-01 8.75871124E-05 0.00000000E+00 1.00000000E+00 2.30671958E-01 2.42291042E+00 0.00000000E+00 1.00000000E+00 6.06877917E-01 1.60277894E-16 0.00000000E+00 ...
7.26 Optimizations: orca_External and setup_orca_opt.py
All SHARC interfaces can deliver gradients for (multiple) ground and excited states in a uniform manner.
This allows in principle to perform optimizations of excited-state minima, conical intersections, or crossing points.
In order to employ a high-quality geometry optimizer for this task, the SHARC suite is interfaced to the external optimizer feature of ORCA.
This is accomplished by providing the script orca_External, which is called by ORCA, runs any of the SHARC interfaces, constructs the appropriate gradient, and returns that to Orca.
For the methodology used to construct the gradients, see section 8.20.
In order to easily prepare the input files for such an optimization, the script setup_orca_opt.py can be used.
It takes a geometry file, interface input files, and the path to ORCA, and creates a directory containing all relevant input files.
In the following, setup_orca_opt.py is described first, because it is the script which the user directly employs. Afterwards, orca_External is specified.
7.26.1 Usage
setup_orca_opt.py is an interactive script, which is started with:
user@host> $SHARC/setup_orca_opt.py
Note that before executing the script you should prepare a template for the interface you want to use (as, e.g., in setup_init.py or setup_traj.py).
7.26.2 Input
In the input section, the script asks for: (i) the path to ORCA, (ii) the input geometries, (iii) the optimization settings, (iv) the interface settings.
Path to ORCA
Here the user is prompted to provide the path to the ORCA directory. Note that the script will not expand the user ( ) and shell variables (since possibly the calculations are running on a different machine than the one used for setup). and shell variables will only be expanded during the actual calculation.
The script works with ORCA 4 and 5.
Interface
In this point, choose any of the displayed interfaces to carry out the ab initio calculations. Enter the corresponding number.
Input geometry
Here the user is prompted for a geometry file in XYZ format, containing one or more geometries (with consistent number of atoms).
For each geometry in this file, a directory with all input files is created, in order to carry out multiple optimizations (e.g., with output from crossing.py).
Number of states
Here the user can specify the number of excited states to be calculated. Note that the ground state has to be counted as well, e.g., if 4 singlet states are specified, the calculation will involve the S0, S1, S2 and S3. Also states of higher multiplicity can be given, e.g. triplet or quintet states.
States to optimize
Two different optimization tasks can be carried out: optimization of a minimum (ground or excited state) or optimization of a crossing point (either a conical intersection between states of the same multiplicity or a minimum-energy crossing points between states of different multiplicities; this is detected automatically).
For minima, the state to optimize needs to be specified.
For crossing points, the two involved states need to be specified.
In all cases, the specified states need to be included in the number of states given before.
CI optimization parameters
If you are optimizing a conical intersection (states of same multiplicity) with an interface which cannot provide nonadiabatic coupling vectors (e.g., SHARC_RICC2.py, SHARC_ADF.py, or SHARC_GAUSSIAN.py), then the optimization will employ the the penalty function method of Levine, Coe, and Martínez [86].
In this method, a penalty function is optimized, which depends on the energies of the two states and on two parameters, σ and α (see section 8.20 for their mathematical meaning).
Practically, the parameters affect how close the minimum of the penalty function is to the true minimum on the crossing seam and how hard the optimization will be to converge.
Generally, a large σ will allow going closer to the true conical intersection, but will make the penalty function more stiff (steeper harmonic) and thus harder to optimize.
A small α will also allow going closer to the true conical intersection, but will make the penalty function less harmonic; at α = 0, the penalty function will have a cusp at the minimum, making it unoptimizable because the gradient never becomes zero.
The default values, 3.5 and 0.02, are the ones suggested in [86].
They can be regarded as relatively soft, i.e., they enable a very smooth convergence but might lead to unacceptably large energy gaps at convergence (i.e., the minimum of the penalty function is too far from the true minimum of the crossing seam).
In this case, it is advisable to restart the optimization from the last point with increased σ (e.g., by a factor of 4), and simultaneously reducing the maximum step (see next point).
The α is best left at the suggested value of 0.02 to avoid the cusp problem.
Maximum allowed displacement
Within ORCA, it is possible to restrict the maximum step (the trust radius) of the optimizer.
A larger maximum step might decrease the number of iterations necessary, but might also lead to instabilities in the optimization (if the potential energy surface is very steep or anharmonic).
Hence, it can be advisable to reduce the maximum allowed step (from the default of 0.3 a.u.), especially if the starting geometry is already very good (e.g., after restart with increase of σ) or if the potential is known to be stiff (strong bond, large σ, small α, …).
Note that the maximum step can be restricted even the penalty function method is not used and σ and α are not relevant.
Interface-specific input
This input section is basically the same as for setup_init.py (sections 7.5.3). Also for the optimizations an initial wave function file should be provided, especially for the multi-reference methods.
Run script setup
Here the user needs to provide the path to the directory where the optimizations should be setup.
7.26.3 Output
Inside the specified directory, setup_orca_opt.py creates one subdirectory for each geometry in the input geometry file.
Each subdirectory is prepared with the corresponding initial geometry file (geom.xyz), the ORCA input file (orca.inp), the appropriate interface-specific files (template, resources, QM/MM), and a shell script for execution (run_EXTORCA.sh).
In order to run one of the optimizations, execute the shell script or send it to a batch queuing system.
Note that $SHARC needs to be added to the $PATH so that ORCA can find orca_External (this is automatically done inside run_EXTORCA.sh).
When the shell script is started, ORCA will write a couple of output files, where the two most relevant are orca.trj and orca.log.
The former is an XYZ file with all geometries from the optimization steps.
The latter (the ORCA standard output) contains all details of the optimization (convergence, step size, etc) as well as a summary of what orca_External did (after the line EXTERNAL SHARC JOB).
This summary contains all relevant energies and shows how the gradient is constructed.
Note that in each iteration, a line starting with is written, which contains the energies of the optimized state(s). This line can easily be extracted with grep to follow the optimization of a crossing point.
7.26.4 Description of orca_External
orca_External provides a connection between the external optimizer of ORCA and any of the SHARC interfaces.
In figure 7.5, the file communication between ORCA, orca_External, and the interfaces is presented.
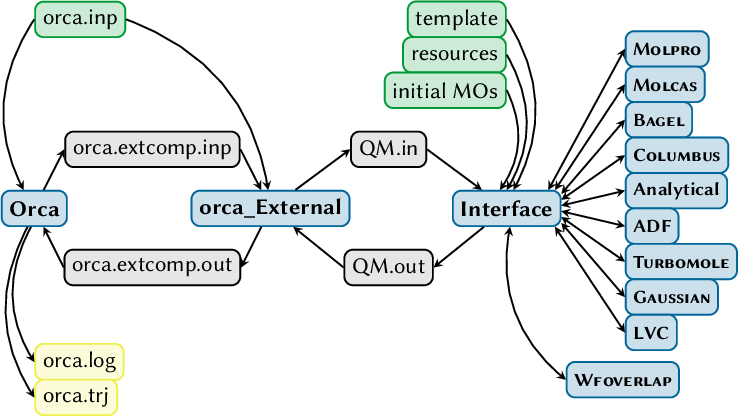
As can be seen, orca_External writes QM.in and QM.out files, in the same way that sharc.x is doing.
All information to write the QM.in file comes from the ORCA communication file orca.extcomp.inp (geometry) and the ORCA input file (number of states, interface, states to optimize).
To provide the latter information, orca_External reads specially marked comments from the ORCA input file which are ignored by ORCA.
These comments start with #SHARC:, followed by a keyword (states, interface, opt, or param) and the keyword arguments.
7.27 Single Point Calculations: setup_single_point.py
It is possible to run single point calculations through the SHARC interfaces.
This is useful, e.g., to do a computation in exactly the same way as during the dynamics simulations.
Single point calculations using the interfaces can also be easily automatized.
7.27.1 Usage
setup_single_point.py is an interactive script, which is started with:
user@host> $SHARC/setup_single_point.py
Note that before executing the script you should prepare a template for the interface you want to use (as, e.g., in setup_init.py or setup_traj.py).
7.27.2 Input
In the input section, the script asks for: (i) the input geometries, (ii) the number of states, and (iii) the interface settings.
Interface
First, choose any of the displayed interfaces to carry out the ab initio calculations. Enter the corresponding number.
Input geometry
Here the user is prompted for a geometry file in XYZ format, containing one or more geometries (with consistent number of atoms).
For each geometry in this file, a directory with all input files is created, in order to carry out multiple optimizations (e.g., with output from crossing.py).
Number of states
Here the user can specify the number of excited states to be calculated. Note that the ground state has to be counted as well, e.g., if 4 singlet states are specified, the calculation will involve the S0, S1, S2 and S3. Also states of higher multiplicity can be given, e.g. triplet or quintet states.
Interface-specific input
This input section is basically the same as for setup_init.py (sections 7.5.3). Also for the optimizations an initial wave function file should be provided, especially for the multi-reference methods.
Run script setup
Here the user needs to provide the path to the directory where the optimizations should be setup.
7.27.3 Output
Inside the specified directory, setup_single_point.py creates one subdirectory for each geometry in the input geometry file.
Each subdirectory is prepared with the corresponding geometry file (QM.in), the appropriate interface-specific files (template, resources, QM/MM), and a shell script for execution (run.sh).
In order to run one of the optimizations, execute the shell script or send it to a batch queuing system.
When the shell script is started, the chosen SHARC interface is executed.
The interface writes a file called QM.log which contains details of the computation and progress status.
The final results of the computation are written to QM.out, which can be inspected manually.
Alternatively, some basic data (excitation energies, oscillator strengths) can be computed with QMout_print.py (section 7.28).
7.28 Format Data from QM.out Files: QMout_print.py
With the script QMout_print.py one can print a table with energies and oscillator strengths from a QM.out file, as it is produced by the interfaces.
7.28.1 Usage
QMout_print.py is a command line tool, and is executed like this:
user@host> $SHARC/QMout_print.py [options] QM.out
The options are summarized in Table 7.13
| Option | Description | Default |
| -h | Display help message and quit. | – |
| -i FILENAME | Path to QM.in file (to read number of states) | – |
| -s INTEGERS | List of numbers of states per multiplicity | 1 |
| -e FLOAT | Absolute energy shift in Hartree | 0.0 |
| -D | Output diagonal states | MCH states |
7.28.2 Output
The script prints a table with state index, state label, energy, relative energy, oscillator strength, and spin expectation value to standard output.
7.29 Diagonalization Helper: diagonalizer.x
The small program diagonalizer.x is used by the Python scripts to diagonalize matrices if the NUMPY library is not available. Currently, only excite.py and SHARC_Analytical.py need to diagonalize matrices. The program diagonalizer.x is implemented as a simple front-end to the LAPACK libary.
The program reads from stdin. The first line consists of the letter “r” or “c”, followed by two integers giving the matrix dimensions. For “r”, the program assumes a real symmetric matrix, for “c” a Hermitian matrix. The matrix must be square.
The second line is a comment and is ignored.
In the following lines, the matrix elements are given. On each line one row of the matrix has to be written. If the matrix is complex, each line contains the double number of entries, where real and imaginary part are always given subsequently.
The following is an example input:
c 2 2 comment 1.0 0.0 2.0 0.1 2.0 -0.1 6.0 0.0
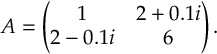 |
(7.6) |
The diagonal matrix and the matrix of eigenvectors is written to stdout.
Chapter 8
Methods and Algorithms
In this chapter different aspects of SHARC simulations are discussed in detail. The topics are ordered alphabetically.
8.1 Absorption Spectrum
Using spectrum.py, an absorption spectrum can be calculated as the sum over the absorption spectra of each individual initial condition:
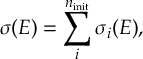 |
(8.1) |
where i runs over the initial conditions.
The spectrum of a single initial condition is the convolution of its line spectrum, defined through a set of tuples (Eα,foscα) for each electronic state α, where Eα is the excitation energy and foscα) is the oscillator strength.
The convolution of the line spectrum can be performed with spectrum.py using either Gaussian or Lorentzian functions. The contribution of a state α to the absorption spectrum σα(E) is given by:
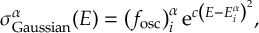 |
(8.2) |
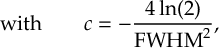 |
(8.3) |
or
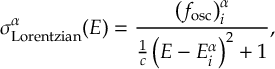 |
(8.4) |
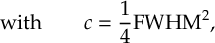 |
(8.5) |
or
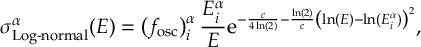 |
(8.6) |
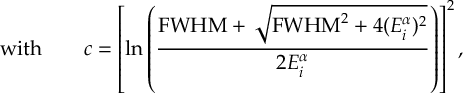 |
(8.7) |
where FWHM is the full width at half maximum.
8.2 Active and inactive states
SHARC allows to “freeze” certain states, which then do not participate in the dynamics. Only energies and dipole moments are calculated, but all couplings are disabled. In this way, these states are never visited (hence also no gradients and nonadiabatic couplings are calculated, making the inclusion of these states cheap). Example:
nstates 2 0 2
actstates 2 0 1
In the example given, state T2 is frozen. The corresponding Hamiltonian looks like:
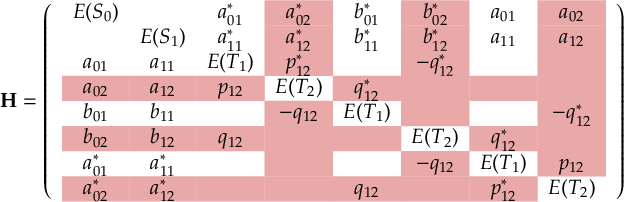 |
(8.8) |
where all matrix elements marked
| red |
are deleted, since T2 is frozen.
The corresponding matrix elements are also deleted from the nonadiabatic coupling and overlap matrices. For propagation including laser fields, also the corresponding transition dipole moments are neglected, while the transition dipole moments still show up in the output (in order to characterize the frozen states).
Active and frozen states are defined with the states and actstates keywords in the input file. Note that only the highest states in each multiplicity can be frozen, i.e., it is not possible to freeze the T1 while having T2 active. However, it is possible to freeze all states of a certain multiplicity.
8.3 Amdahl’s Law
Some of the interfaces (SHARC_MOLCAS.py, SHARC_ADF.py SHARC_GAUSSIAN.py, SHARC_ORCA.py) use Amdahl’s law to predict the most efficient way to run multiple calculations in parallel, where each calculation itself is parallelized.
For example, in SHARC_GAUSSIAN.py it might be necessary to compute the gradients of five states, using four CPU cores.
The most efficient way to run these five jobs depends on how well the GAUSSIAN computation scales with the number of cores-for bad scaling, running four jobs on one core each followed by the fifth job might be best, whereas for good scaling, running each job on four cores subsequently is better because no core is idle at any time.
In order to automatically distribute the jobs efficiently, the interfaces use Amdahl’s law, which can be stated as:
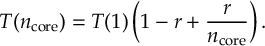 |
(8.9) |
Here, T(1) is the run time of the job with one CPU core, and r is the fraction of T(1) which benefits from parallelization.
The parameter r can be given to the interfaces; it is between 0 and 1, where 0 means that the calculation does not get faster at all with multiple cores, whereas 1 means that the run time scales linearly with the number of cores.
8.4 Bootstrapping for Population Fits
Bootstrapping, in the context of population fitting, is a statistical method to obtain the statistical distribution of the fitted parameters, which can be used to infer the error associated with the fitted parameter.
The general idea of bootstrapping is to take the original sample (the set of trajectories in the ensemble), and generate new samples (resamples) by randomly drawing trajectories “with replacement” from the original ensemble.
These resamples will differ form the original ensemble by containing some trajectories multiple times while other trajectories might be missing.
For each of the resamples, the fitting parameter are obtained normally and saved for later analysis.
After many resamples, we obtain a list of many “alternative” parameters, which can be plotted in a histogram to see the statistical distribution of the fitting parameter.
The number of resamples should generally be large (several hundred or thousand resamples), although with bootstrap.py, one can inspect the convergence of the fitting parameters/errors to decide how many resamples are sufficient.
From the computed list of parameters, error measures can be computed.
Assume that {xi} is the set of fitting parameters obtained.
bootstrap.py and make_fit.py compute the arithmetic mean and standard deviation like this:
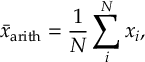 |
(8.10) |
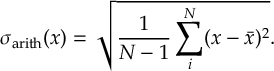 |
(8.11) |
Because the distribution of {xi} might be skewed (e.g., contains some very large values but few very small ones), the script also computes the geometric mean and standard deviation like this:
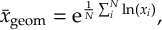 |
(8.12) |
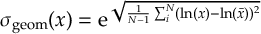 |
(8.13) |
Note that the geometric standard deviation is a dimensionless factor (unlike the arithmetic standard deviation, which has the same dimension as the mean).
Therefore, within bootstrap.py and make_fit.py the geometric errors are always displayed with separate upper and lower bounds as ―x\substack+―x(σ(x)−1) −―x(1/σ(x)−1).
Note that bootstrap.py and make_fit.py will always report one times the standard deviation in the output.
If larger confidence intervals are desired, simply multiply the arithmetic error as usual.
For the geometric error, use for example ―x\substack+―x(σ(x)2−1) −―x(1/σ(x)2−1).
8.5 Computing electronic populations
The electronic populations from SHARC trajectories can be obtained in different ways.
This is primarily due to the fact that in surface hopping one could either consider the active state or the electronic wave function coefficients.
This issue is discussed in detail in [35], where it is shown that the optimal way to obtain the electronic populations is actually a combination of both kinds of information in a Wigner-like transformation.
Hence, there are three options in SHARC: (i) based on classical active state, (ii) based on electronic wave function coefficients, and (iii) based on Wigner-transform.
Additionally, the populations can be analyzed in different representations (diagonal, MCH, diabatic).
Diagonal representation
The diagonal representation, there is no basis transformation involved, and hence the equations are very simple.
For a single trajectory, the three possible populations can be obtained by:
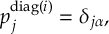 |
(8.14) |
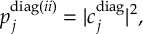 |
(8.15) |
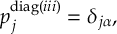 |
(8.16) |
where α is the active diagonal state.
MCH representation
To obtain the MCH representation, one needs to transform the populations with the matrix U.
Hence, one obtains:
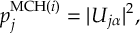 |
(8.17) |
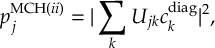 |
(8.18) |
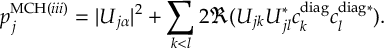 |
(8.19) |
Diabatic representation
To obtain the diabatic representation, one needs to transform the populations with the appropriate transformation matrix T, which in SHARC is obtained as the matrix product of reference overlap matrix, time-ordered overlap matrices, and U for the current time step.
Hence, one obtains:
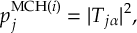 |
(8.20) |
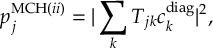 |
(8.21) |
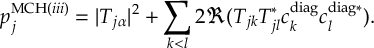 |
(8.22) |
8.6 Damping
If damping is activated in SHARC (keyword dampeddyn), in each time step the following modification to the velocity vector is made
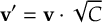 |
(8.23) |
where C is the damping factor given in the input. Hence, in each time step the kinetic energy is modified by
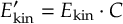 |
(8.24) |
The damping factor C must be between 0 and 1.
8.7 Decoherence
In surface hopping, without any corrections the coherence between the states is usually too large [21]. A trajectory in state β, but where state α has a large coefficient, will still travel according to the gradient of state β. However, the gradients of state α are almost certainly different to the ones of state β. As a consequence, too much population of state α is following the gradient of state β. Decoherence corrections damp in different ways the population of all states α ≠ β, so that only population of β follows the gradient of state β.
Currently, in SHARC there are two decoherence corrections implemented, “energy-based decoherence”, or EDC, as given in [116] and “augmented fewest-switches surface hopping”, or AFSSH, as described in [30].
8.7.1 Energy-based decoherence
In this scheme, after the surface hopping procedure, when the system is in state β, the coefficients are updated by the following relation
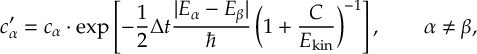 |
(8.25) |
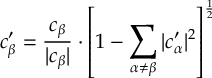 |
(8.26) |
where C is the decoherence parameter. The decoherence correction can be activated with the keyword decoherence in the input file. The decoherence parameter C can be set with the keyword decoherence_param (the default is 0.1 hartree, as suggested in [116]).
8.7.2 Augmented FSSH decoherence
Augmented FSSH by Subotnik and coworkers is described in [30].
For SHARC, the augmented FSSH algorithm was adjusted to the case of the diagonal representation.
The basic idea is that besides the actual trajectory, the program maintains an auxiliary trajectory for each state.
The auxiliary trajectories are propagated using the gradients of the associated (not active) state, and because the gradients are different, the auxiliary trajectories eventually diverge from each other and from the main trajectory.
From this diverging, one can compute decoherence rates which can be used to stochastically set the electronic coefficients of the diverging state to zero.
First, we compute two matrices:
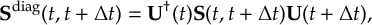 |
(8.27) |
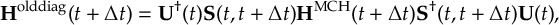 |
(8.28) |
where S is the overlap matrix, as used in 8.33.
Hence, Sdiag(t,t+∆t) is the overlap matrix in the diagonal basis and Holddiag(t+∆t) is the Hamiltonian at time t+∆t expressed in the diagonal basis of time step t.
We then propagate the auxiliary trajectories for each state j, considering that the active state is α.
For this, we need the gradient matrix Gdiag from section 8.11.
We define:
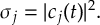 |
(8.29) |
We do the X step of the velocity-Verlet algorithm:
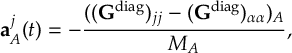 |
(8.30) |
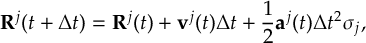 |
(8.31) |
where A goes over the atoms.
Then, we compute the new gradient:
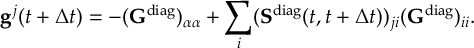 |
(8.32) |
We then carry out the v step:
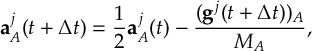 |
(8.33) |
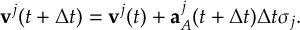 |
(8.34) |
We then perform a diabatization of the auxiliary trajectories (e.g., for a trivially avoided crossing, the moments between the crossing states are interchanged):
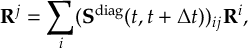 |
(8.35) |
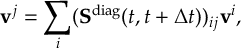 |
(8.36) |
 |
(8.37) |
to transform the data back into the adiabatic basis at time t+∆t.
Finally, we carry out the decoherence correction procedure for each auxiliary trajectory.
We compute the displacement from the auxiliary trajectory of the active state:
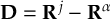 |
(8.38) |
We compute two rate constants:
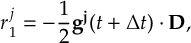 |
(8.39) |
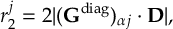 |
(8.40) |
or if no nonadiabatic coupling vectors are available:
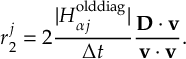 |
(8.41) |
We draw a random number (identical for all states) r between 0 and 1.
If r < ∆t(rj1−rj2), then we collapse state j, by setting its coefficient to zero and enlarging the coefficient of the active state such that the total norm is conserved; we also set the moments Rj and vj to zero.
If no collapse occurred, if r < −∆t rj1, we set the moments Rj and vj to zero.
After a surface hop occurred, we reset all auxiliary trajectories.
8.8 Essential Dynamics Analysis
As an alternative to normal mode analysis (see section 8.19), essential dynamics analysis can be used to identify important modes in the dynamics.
This procedure is a principal component analysis of the geometric displacements.[83,[82]
Unlike normal mode analysis, it does not depend on the availability of the normal mode vectors.
The covariance matrix is computed from the following equation (μ and ν are indices over the 3Natom degrees of freedom):
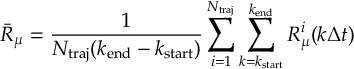 |
(8.42) |
and
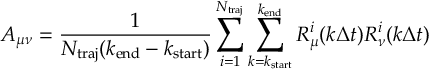 |
(8.43) |
as a matrix C with elements:
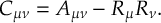 |
(8.44) |
Diagonalization of the symmetric matrix C gives a set of eigenvalues and eigenvectors.
The eigenvectors represent the essential dynamics modes, and the corresponding eigenvalues are the variances of the modes.
Modes with large variances show strong motion in the dynamics, whereas small variances are found for modes which show weak motion.
Because the modes are uncorrelated, the few modes with the largest variance describe most of the molecular motion, which shows that essential dynamics analysis can be used to for data reduction.
8.9 Excitation Selection
excite.py can select initial active states for the dynamics based on the excitation energies Ek,α and the oscillator strengths fosck,α for each initial condition k and excited state α.
First, for all excited states of all initial conditions, the maximum value pmax of
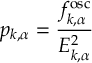 |
(8.45) |
is found. Then for each excited state, a random number rk,α is picked from [0,1]. If
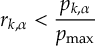 |
(8.46) |
then the excited state is selected as a valid initial condition. This excited-state selection scheme is taken from [121].
Within excite.py it is possible to restrict the selection to a subset of all excited states (only certain adiabatic states/within a given energy range). In this case, also pmax is only determined based on this subset of excited states.
8.9.1 Excitation Selection with Diabatization
The active states can be selected based on a diabatization.
This necessitates the wave function overlaps between a reference geometry (ICOND_00000/) and the current initial condition k.
The overlap matrix with elements
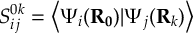 |
(8.47) |
can be computed with wfoverlap.x (calculations can be setup with setup_init.py).
This overlap matrix is rescaled during the excitation selection procedure such S0k11 is equal to one (by dividing all elements by |S0k11|2).
Then, assume we want to start all trajectories in the state which corresponds to state x at the reference geometry.
The excitation selection will select a state y as initial state if S0kxy > 0.5.
8.10 Global fits and kinetic models
In this section, we specify the basic assumptions of the chemical kinetic models used with the scripts make_fitscript.py and make_fit.py and the globals fits of these models to data.
8.10.1 Reaction networks
The kinetic models used by make_fitscript.py and make_fit.py are based on a chemical reaction network, where chemical species react via unimolecular reactions.
The reaction networks allowed in the script are a simple directed graphs, where the species are the vertices and the reactions are the directed edges.
Each reaction is characterized by an associated rate constant and connects exactly one reactant species to exactly one product species.
In order to obtain rate laws which can be integrated easily, there are a number of restrictions imposed on the network graphs.
Some restrictions and possible features of the graphs are depicted exemplarily in Figure 8.1.
First, each species and each reaction rate needs to have a unique label.
There cannot be two species with the same label, but there can be two reactions with the same reaction rate constant.
Second, the graph must be a simple directed graph, hence there cannot be any (self-) loops or more than one reaction with the same initial and the same final species.
All restrictions marked as “Not allowed” in the Figure are enforced in the input dialogue of make_fitscript.py
However, back reactions are allowed (as a back reaction has a different initial and a different final species as the corresponding reaction).
Except from these restrictions, the graph may contain combinations of sequential and parallel reactions.
The graph may also be disjoint, i.e., it can be the union of several independent sub-networks.
Disjoint graphs with repeated reaction labels can be useful to fit population data from ensembles with identical settings but different initial conditions (in this case, merge the population files with paste before starting the fit.
There are two kinds of cycles possible, called here parallel pathways and closed walks.
Parallel pathways are independent sequences of reactions with the same initial and final species (e.g., A→ C and A→ B→ C).
A closed walk is a sequence of reactions where the initial species is equal to the final species.
These cycles can sometimes lead to problems.
If you use make_fitscript.py, then it is necessary that the system of differential equations of the rate laws can be integrated in closed form by MAXIMA.
Since make_fit.py solves the differential equation system numerically, it is not necessary that the solution can be given in closed form.
However, cycles can also lead to problems in the fitting procedure (rate constants in parallel pathways can be strongly correlated and cause large errors and bad convergence in fitting).
An example reaction network graph is shown in Figure 8.2.
In this graph, there are 5 species (S2, S1, S0, T2, and T1) and 6 reactions, each with a rate constant (kS, kRlx, k22, k11, k21, k12).
This graph shows some features which are allowed in the reaction networks for make_fitscript.py: sequential reactions, parallel reactions, back reactions, and converging reaction pathways.
Note that this reaction network is likely to cause problems in the fitting step (large errors).
8.10.2 Kinetic models
Based on the reaction network graph, a system of differential equations describing the rate laws of all species can be setup.
The system of equations (equivalently, the matrix differential equation) can be written as:
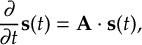 |
(8.48) |
where s is the vector of the time-dependent populations of each species and A is the matrix containing the rate constants.
In order to construct A, start with A=0 and, for each reaction from species i to species j with rate k, substract k from Aii and add k to Aji.
In order to integrate this system of equations, in practice one also needs to define initial conditions.
In the present context, the initial conditions are fully specified by s(t=0)=s0, where s0 are constant expressions defined by the user.
Solving (8.48) yields (in not too complicated cases) the closed-form expressions for the functions s(t), which contain as parameters all rate constants k and all initial values s0.
8.10.3 Global fit
Suppose there is a data set p(t)=(p1(t),p2(t),…) of time-dependent populations of several states k=1,2,… and which is given at several points of time {ti: 0 < ti < tmax}.
We can fit to one data set pk(t) a function sl(t) from s(t) by optimizing the parameters (mainly the rate constants) such that ∑i |pk(ti)−sl(ti)|2 becomes minimal.
In order to perform global fit including several species l and several states k, we construct piecewise global functions from p(t) and s(t) and then optimize the parameters accordingly.
8.11 Gradient transformation
8.11.1 Nuclear gradient tensor transformation scheme
Since the actual dynamics is performed on the PESs of the diagonal states, also the gradients have to be transformed to the diagonal representation. To this end, first a generalized gradient matrix GMCH is constructed from the gradients gMCHα=−∇RHααMCH
and the nonadiabatic coupling vectors
KβαMCH:
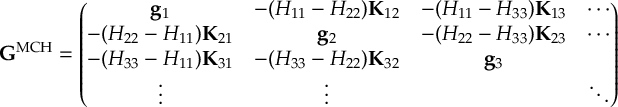 |
(8.49) |
Note that all quantities in the matrix are in the MCH representation, the superscripts were omitted for brevity.
The matrix GMCH is subsequently transformed into the diagonal representation, using the transformation matrix U:
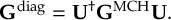 |
(8.50) |
The diagonal elements of Gdiag now contain the gradients of the diagonal states, while the off-diagonal elements contain the scaled nonadiabatic couplings −(Hdiagββ−Hdiagαα)Kβαdiag. The gradients are needed in the Velocity Verlet algorithm in order to propagate the nuclear coordinates. The nonadiabatic couplings are necessary if the velocity vector is to be rescaled along the nonadiabatic coupling vector.
Since the matrix GMCH contains elements which are itself vectors with 3N components, the transformation is done component-wise (e.g. first a matrix Gx,atom 1 is constructed from the x components of all gradients (and nonadiabatic couplings) for atom 1, this matrix is transformed and written to the x, atom 1 component of Gdiag, then this is repeated for all components).
Since the calculation of the nonadiabatic couplings KMCHβα might add considerable computational cost, there is the input keyword nogradcorrect which tells SHARC to neglect the KMCHβα in the gradient transformation.
From SHARC3.0 onwards, this scheme is called nuclear gradient tensor scheme, or NGT scheme. The NGT scheme can be turned on by using keyword gradcorrect alone, or followed by options, i.e. gradcorrect ngt.
8.11.2 Time derivative matrix transformation scheme
Alternatively, one can obtain the energy conserving force in diagonal representation by using the time derivative matrix scheme, or TDM scheme. In TDM scheme, no computation of nonadiabatic coupling vectors are required, and therefore it is more efficient. And TDM is especially recommended for overlap-based algorithms and curvature-driven algorithms because one of the advantages of these algorithms is that they do not require computating of nonadiabatic coupling vectors. See section 8.34.
One can turn on TDM scheme by using keyword gradcorrect tdm
The TDM scheme utilizes the time derivative matrix KGB, with matrix elements given by
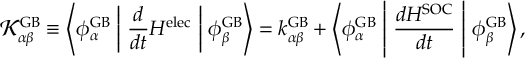 |
(8.51) |
where GB denotes that this is a general basis which can be either diagonal or MCH representation, superscript SOC denotes the spin-orbit coupling terms, and
 |
(8.52) |
where superscript SF denotes spin-free.
One can show that,
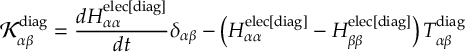 |
(8.53) |
and
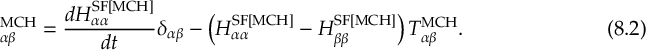 |
(8.54) |
Similar as in the NGT scheme, we now neglect [d/dt]HSOC. This gives the TDM scheme
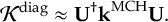 |
(8.55) |
Therefore,
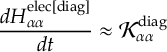 |
(8.56) |
and
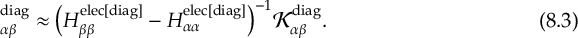 |
(8.57) |
This is very useful, because it allows us to compute [(dHelec[diag]αα)/dt] without computing nonadiabatic coupling vectors.
One can show that the only requirement a diagonal gradient needs to be fulfilled to conserve energy is,
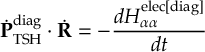 |
(8.58) |
where · PdiagTSH is the diagonal force. Therefore, by knowing [(dHelec[diag]αα)/dt] one can obtain an alternative energy conserving force as
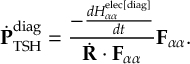 |
(8.59) |
The above diagonal force conserves energy for any real and nonzero vector Fαα that is not normal to · R. In SHARC3.0, we use the following physically motivated choice of Fαα
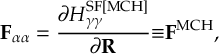 |
(8.60) |
where state γ is a state in the MCH basis that corresponds to state α in the diagonal basis.
In SHARC3.0, the default is to use different approaches to compute [(dHelec[diag]αα)/dt] for different algorithms. For overlap-based algorithms,
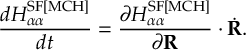 |
(8.61) |
This defines kMCH for overlap-based algorithm, and one transform kMCH to Kdiag with equation (8.55). This is called gradient approach, and can be turned on by using keyword tdm_method gradient.
The default for curvature-driven algorithms is that we employ finite differences to compute both [(dHSF[MCH]αα)/dt] and [(dHelec[diag]αα)/dt]. For the first and second time steps, we use first-order backward finite differences
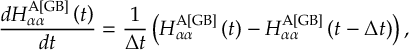 |
(8.62) |
where superscript A can be SOC, SF, or elec (full Hamiltonian, includong both SF and SOC).
And for later steps, we use second-order backward finite differences
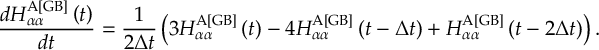 |
(8.63) |
This is called the energy approach, and can be turned on by using keyword tdm_method energy.
8.11.3 Dipole moment derivatives
For strong laser fields, the derivative of the dipole moments might be a non-negligible contribution to the gradients. In this case, they should be included in the gradient transformation step:
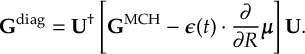 |
(8.64) |
This can be activated with the keyword dipole_grad in the SHARC input file.
8.12 Internal coordinates definitions
In this section, the internal coordinates available in geo.py are defined.
Bond length
The bond length between two atoms a and b is:
 |
(8.65) |
Bond angle
The bond angle for atoms a, b and c is defined as the angle
 |
(8.66) |
where vba is the vector from atom b to atom a.
Dihedral
The dihedral angle is defined via the vectors w1 and w2:
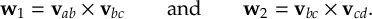 |
(8.67) |
The dihedral is given as the angle between w1 and w2 according to equation (8.66).
In order to distinguish left- and right-handed rotation, also the vector Q=w1×w2 is computed, and if the angle between Q and vbc is larger than 90° then the value of the dihedral is multiplied by -1.
Pyramidalization angle
The pyramidalization angle is defined via the vectors vba and
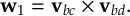 |
(8.68) |
The pyramidalization angle is then given as 90° − θ(vba,w1).
This definition of the pyramidalization angle works best for nearly planar arrangements, like in amino groups.
An alternative definition of the pyramidalization angle works better for strongly pyramidalized situations (e.g., fac-arranged atoms in a octahedral metal complex).
This pyramidalization angle is defined as 180° minus the angle between vab and the average of vbc and vbd.
Cremer-Pople parameters
The definitions of the Cremer-Pople parameters for 5- and 6-membered rings is described in [79].
Boeyens classification
For 6-membered rings, the Boeyens classification scheme is described in [80].
Angle between two rings
In order to compute angles between the mean planes of two rings, we compute the normal vector of the two rings as in [79].
We then compute the angle between the two normal vectors.
8.13 Kinetic energy adjustments
There are several options how to adjust the kinetic energy after a surface hop occurred. The simplest option is to not adjust the kinetic energy at all (input: ekincorrect none), but this obviously leads to violation of the conservation of total energy.
Alternatively, the velocities of all atoms can be rescaled so that the new kinetic energy and the potential energy of the new state β again sum up to the total energy.
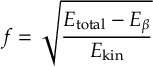 |
(8.69) |
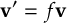 |
(8.70) |
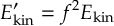 |
(8.71) |
Within this methodology, when the energy of the old state α was lower than the energy of the new state β the kinetic energy is lowered. Since the kinetic energy must be positive, this implies that there might be states which cannot be reached (their potential energy is above the total energy). A hop to such a state is called “frustrated hop” and will be rejected by SHARC. Rescaling parallel to the nuclear velocity vector is requested with ekincorrect parallel_vel.
Alternatively, according to Tully’s original formulation of the surface hopping method [14], after a hop from α to β only the component of the velocity along the direction of the nonadiabatic coupling vector Kβα should be rescaled. With
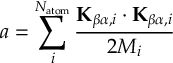 |
(8.72) |
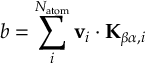 |
(8.73) |
the available energy can be calculated:
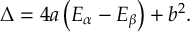 |
(8.74) |
If ∆ < 0, the hop is frustrated and will be rejected. Otherwise, the scaled velocities v′ can be calculated as
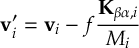 |
(8.75) |
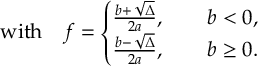 |
(8.76) |
This procedure can be requested with ekincorrect parallel_nac. Note that in this case SHARC will request the nonadiabatic coupling vectors, even if they are not used for the wave function propagation.
8.13.1 Reflection for frustrated hops
As suggested by Tully [14], during a frustrated hop one might want to reflect the trajectory (i.e., invert some component of the velocity vector).
In SHARC, there are three possible options to this, the first being no reflection (reflect_frustrated none).
Alternatively, one can invert the total velocity vector v:=−v (reflect_frustrated parallel_vel).
As this leads to a nearly complete time reversal and might be inappropriate, as a third option one can choose to only reflect the velocity component parallel to the nonadiabatic coupling vector between the active state and the state to which the frustrated hop was attempted.
The condition for reflection in this case is based on three scalar products:
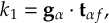 |
(8.77) |
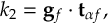 |
(8.78) |
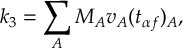 |
(8.79) |
Reflection is only carried out if k1k2 < 0 and k2k3 < 0.
In order to reflect, we compute:
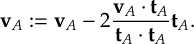 |
(8.80) |
where tA is the component of tαf corresponding to atom A.
8.13.2 Choices of momentum adjustment direction
In addition to previously mentioned choices of vectors to adjustment momentum, namely, velocity vector, and nonadiabatic coupling vector, in SHARC3.0 we have several new choices of momentum adjustment vectors. A complete list includes: velocity vector,
projected velocity vector (vibrational velocity vector),
nonadiabatic coupling vector,
projected nonadiabatic coupling vector,
difference gradient vector,
effective nonadiabatic coupling vector,
and projected effective nonadiabatic coupling vector.
Note that using the projected vectors is recommended choice because these vectors can conserve angular momentum and center of mass motion. Section 8.31 introduces the effective nonadiabatic coupling vector, and Section 8.14 introduces the projection operator.
Section 8.34 distinguishes different types of nonadiabatic dynamics algorithms based on the coupling types to be computed. Although using nonadiabatic coupling vector as momentum adjustment direction is most accurate, one of the advantages of not using nonadiabatic coupling vector as momentum adjustment direction is that one can utilize the advantages of overlap-based algorithms and curvature-driven algorithms that nonadiabatic coupling vector is not needed in propagating electronic and nuclear equations of motion.
8.14 Projection operator
The projection operator projects out the translational and rotational components of a vector, i.e., nonadiabatic coupling vector (NAC vector). The projected NAC, is expressed as
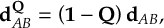 |
(8.81) |
where 1 and Q are the identity operator and projection operator, respectively, and A and B are indices of electronic states.
The projection operator is a 3N×3N matrix with elements
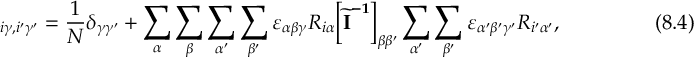 |
(8.82) |
where indices i and i’ label the nuclei and vary from 1 to N, α, β, γ, α‘, β‘, and γ‘ take on the values x, y, and z.
~I −1 is the inverse of matrix ~I.
Matrix ~I is same as moment of inertia matrix with all masses set to 1, and \varepsilonup is the completely antisymmetric third-order unit pseudotensor, whose elements are the Levi-Civita symbols.
The first term of the projection operator projects onto the three directions corresponding to overall translation, and the second term projects onto the three directions corresponding to overall rotation.
8.15 Fewest switches with time uncertainty
The fewest switches with time uncertainty (FSTU) propagation is identical to the FS algorithm except when there is a frustrated hop. The FSTU looks for nonlocal hops to reduce the number of frustrated hops.
At time t, the FSTU algorithm computes the potential energy differences between the active state K and the rest of the states,
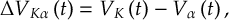 |
(8.83) |
where Vα(t) is the adiabatic potential energy of state α at time t. In SHARC3.0, the velocity is rescaled after a K→ α hop according to
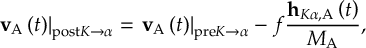 |
(8.84) |
where vA, hKα,A, and MA are respectively the velocity vector, momentum adjustment vector, and the atomic mass of atom A, and f is a unitless factor to be computed.
The factor f is computed by requiring energy conservation after a hop
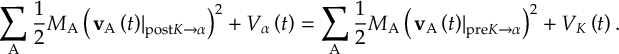 |
(8.85) |
Therefore,
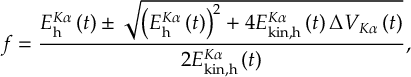 |
(8.86) |
where
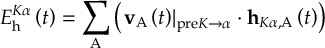 |
(8.87) |
and
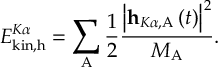 |
(8.88) |
To have a real solution of f, the following condition must be fulfilled:
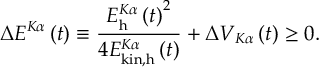 |
(8.89) |
At time t0, when one encounters a K→ β hop that is frustrated by the FS algorithm, one computes the FSTU uncertainty time for this unconfirmed hop as
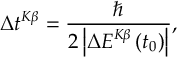 |
(8.90) |
where the absolute value is needed because ∆EKβ(t0) is negative. Then FSTU algorithm looks for energy accessible K→ β hop within this time uncertainty region.
8.16 Laser fields
The program laser.x can calculate laser fields as superpositions of several analytical, possibly chirped, laser pulses. In the following, the laser parametrization is given (see [122] for further details).
8.16.1 Form of the laser field
In general, the laser field ϵ(t) is a linear superposition of a number of laser pulses li(t):
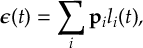 |
(8.91) |
where pi is the normalized polarization vector of pulse i.
A pulse l(t) is formed as the product of an envelope function and a field function.
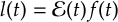 |
(8.92) |
8.16.2 Envelope functions
There are two types of envelope function defined in laser.x, which are Gaussian and sinusoidal.
The Gaussian envelope is defined as:
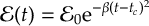 |
(8.93) |
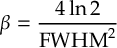 |
(8.94) |
where E0 is the peak field strength, FWHM is the full width at half maximum and tc is the temporal center of the pulse.
The sinusoidal envelope is defined as:
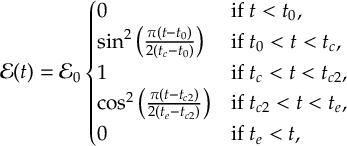 |
(8.95) |
where again E0 is the peak field strength, t0 and tc define the interval where the field strength increases, and tc2 and te define the interval where the field strength decreases. Figure 8.3 shows the general form of the envelope functions and the meaning of the temporal parameters t0, tc, t2c and te.
8.16.3 Field functions
The field function f(t) is defined as:
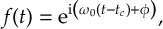 |
(8.96) |
where ω0 is the central frequency and ϕ is the phase of the pulse. Even though the laser field is complex in this expression, in the propagation of the electronic wave function in SHARC only the real part is used.
8.16.4 Chirped pulses
In order to apply a chirp to the laser pulse l(t), it is first Fourier transformed to the frequency domain, giving the function ~l(ω). The chirp is applied by calculating:
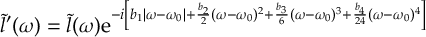 |
(8.97) |
The chirped laser in the time domain l′(t) is then obtained by Fourier transform of the chirped pulse ~l′(ω).
8.16.5 Quadratic chirp without Fourier transform
If laser.x was compiled without the FFTW package, the only accessible chirps are quadratic chirps for Gaussian pulses:
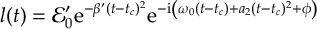 |
(8.98) |
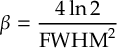 |
(8.99) |
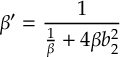 |
(8.100) |
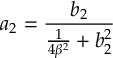 |
(8.101) |
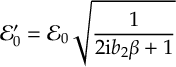 |
(8.102) |
Other chirps are only possible with the Fourier transformation.
8.17 Laser interactions
The laser field ϵ is included in the propagation of the electronic wave function. In each substep of the propagation, the interaction of the laser field with the dipole moments is included in the Hamiltonian. The contribution Vi is in each time step added to the Hamiltonian in equations (8.177) or (8.182), respectively:
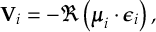 |
(8.103) |
 |
(8.104) |
 |
(8.105) |
where i, n t and ∆t are defined as in section 8.33.
8.17.1 Surface Hopping with laser fields
If laser fields are present, there can be two fundamentally different types of hops: laser-induced hops and nonadiabatic hops. The latter ones are the same hops as in the laser-free simulations, and demand that the total energy is conserved. The laser-induced hops on the other hand demand that the momentum (kinetic energy) is conserved. Hence, SHARC needs to decide for every hop whether it is laser-induced or not.
Consider a previous state α and a new state β. Currently, the hop is classified based on the energy gap ∆E=|Eβdiag−Eαdiag| and the instantaneous central energy of the laser pulse ω.
The hop is assumed to be laser-induced if
 |
(8.106) |
where W is a fixed parameter. W can be set using the input keyword laserwidth.
If a hop has been classified as laser-free, the momentum is adjusted according to the equations given in section 8.13.
8.18 Linear Vibronic Coupling Models
In the vibronic coupling model [120] the diabatic energy and coupling matrix V is constructed as
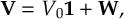 |
(8.107) |
where V0 is the reference potential and W includes the state-specific vibronic terms.
Within SHARC, the reference potential is chosen to be harmonic.
The reference potential is expressed in dimensionless mass-frequency-scaled normal coordinates, which can be computed from the Cartesian coordinates rA as
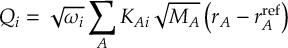 |
(8.108) |
where ωi is the frequency of normal mode i, MA is an atomic mass, and KA i denotes the conversion matrix between mass-weighted Cartesian and normal coordinates.
Using these coordinates, the harmonic reference potential is given as
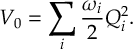 |
(8.109) |
In the case of the linear vibronic coupling model, one additionally considers the following state-specific terms that constitute the W matrix.
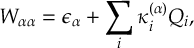 |
(8.110) |
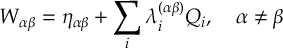 |
(8.111) |
Here the ϵα are the vertical excitation energies, the ηαβ are the SOC constants, and the κi(α) and λi(αβ) are termed intrastate and interstate vibronic coupling constant [120].
8.18.1 Obtaining LVC parameters from ab initio data
All LVC parameters are either constant or linear, implying that they can be obtained from either a single ab initio computation or from some first derivative.
The following equations show how the parameters ϵα, ηαβ, κi(α), and λi(αβ) are obtained.
The parameters ϵα are simply the vertical excitation energies at the reference geometry:
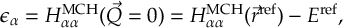 |
(8.112) |
where Eref is some reference energy.
Likewise, the SOC parameters ηαβ are simply the SOC matrix elements at the reference geometry:
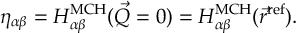 |
(8.113) |
These two equations hold because in the LVC model we assume that at the reference geometry diabatic basis and MCH basis coincide.
The intrastate linear vibronic coupling term κi(α) is the gradient of the diabatic energy of state n.
Since at the reference geometry, diabatic and MCH basis coincide, this is equivalent to the gradient of the corresponding MCH state.
This gradient needs only be transformed from Cartesian coordinates into normal mode coordinates:
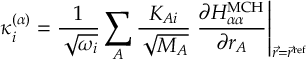 |
(8.114) |
The interstate linear vibronic coupling term λi(αβ) is the gradient of the diabatic coupling between states n and m.
If analytical nonadiabatic coupling vectors are available, these parameters can be obtained-similarly as the κi(α) parameters-by coordinate transformation of the energy-difference-scaled nonadiabatic coupling vector:
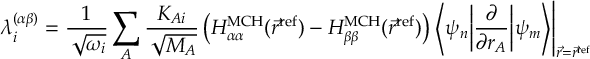 |
(8.115) |
If gradients or nonadiabatic coupling vectors are not available, then the κi(α) and λi(αβ) parameters can be obtained numerically.
To this end, one performs ab initio calculations at displaced geometries ±δQi, where
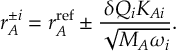 |
(8.116) |
The ab initio calculations at these geometries provide the energies HMCHαα(rA±i) and the wave function overlaps S±iαβ=〈ψMCHα(→rref)|ψMCHβ(→r±i)〉.
From these data, the κi(α) values can be computed as:
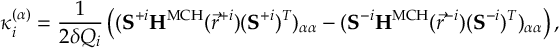 |
(8.117) |
and the λi(αβ) as:
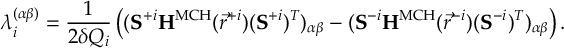 |
(8.118) |
8.19 Normal Mode Analysis
The normal mode analysis can be used to find important vibrational modes in the excited-state dynamics.[81,[82]
Given a matrix Q containing the normal mode vectors and a reference geometry Rref, calculate for each trajectory
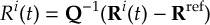 |
(8.119) |
to obtain the displacements in normal mode coordinates.
Averaging over the displacements gives the average trajectory:
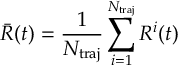 |
(8.120) |
which should contain only coherent motion, since random motion cancels out in an ensemble.
A measure for the coherent activity in a mode is the standard deviation (over time) of the average trajectory:
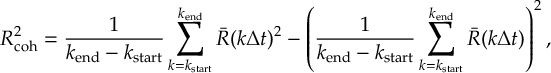 |
(8.121) |
where kstart and kend are the start and end time steps for the analysis.
Rcoh a vector with one number per normal mode, where larger number mean that there is more coherent activity in this mode.
A measure for the total motion in a mode is the total standard deviation:
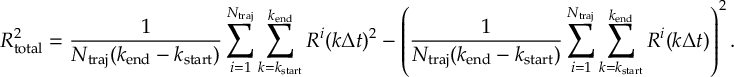 |
(8.122) |
8.20 Optimization of Crossing Points
With orca_External it is possible to optimize different kinds of crossing points.
In all cases, these optimizations involve the energies of the lower state El and upper state Eu, the energy difference ∆E=Eu−El, the gradients of the lower state gl and upper state gu, the gradient difference vector d, and/or the nonadiabatic coupling vector t.
The simplest case is the optimization of minimum-energy crossing points between states of different multiplicity, because in this case the nonadiabatic coupling vector is zero and the branching space is one-dimensional.
In this case [85], the energy to optimize is Eu inside the intersection space, and ∆E inside the branching space.
The corresponding gradient to follow F can be written as:
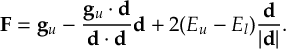 |
(8.123) |
More complicated is the optimization of a conical intersection, between states of the same multiplicity, because the branching space is two-dimensional.
The corresponding gradient to follow F is:
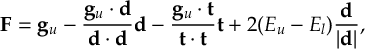 |
(8.124) |
where d and t need to be orthogonalized.
If no nonadiabatic coupling vector is available because the interface cannot deliver them, conical intersections are optimized with the penalty function method of Levine et al. [86].
The effective energy to optimize is defined as:
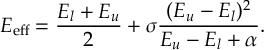 |
(8.125) |
This equation is a combination of the two main targets of the optimization, the average energy and the energy gap.
The parameter σ allows prioritizing either of the two, with a larger σ leading to smaller energy gaps.
The parameter α is there to avoid the discontinuity at Eu=El.
The corresponding gradient to follow F is:
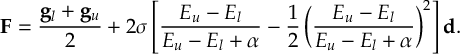 |
(8.126) |
Note that σ and α might strongly influence the quality (i.e., with the penalty function method the optimization will not converge to the true minimum energy conical intersection point) of the result and the convergence behavior.
A large σ and a small α will improve the quality of the result, but make the optimization harder to converge.
8.21 Phase tracking
8.21.1 Phase tracking of the transformation matrix
A Hermitian matrix HMCH can always be diagonalized. Its eigenvectors form the rows of a unitary matrix U, which can be used to transform between the original basis and the basis of the eigenfunctions of H.
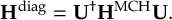 |
(8.127) |
However, the condition that U diagonalizes HMCH is not sufficient to define U uniquely. Each normalized eigenvector u can be multiplied by a complex number on the unit circle and still remains a normalized eigenvector.
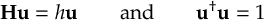 |
(8.128) |
leads to
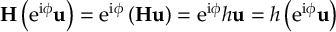 |
(8.129) |
and
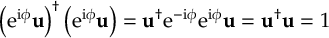 |
(8.130) |
Thus, for all diagonal matrices Φ with elements
δβαexp(iϕβ),
also the matrix U′=UΦ diagonalizes HMCH (if U diagonalizes it).
The propagation of the coefficients in the diagonal basis is written as (see section 8.33):
 |
(8.131) |
where U(t) and U(t+∆t) are determined independently from diagonalizing the matrices HMCH(t) and HMCH(t+∆t), respectively. However, depending on the implementation of the diagonalization, U(t) and U(t+∆t) may carry unrelated, random phases. Even if HMCH(t) and HMCH(t+∆t) were identical, U(t) and U(t+∆t) might still differ, e.g.:
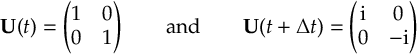 |
(8.132) |
The result is that the coefficients c pick up random phases during the propagation, leading to random changes in the direction of population transfer, invalidating the whole propagation.
In order to make the phases of U(t) and U(t+∆t) as similar as possible, SHARC employs a projection technique. First, we define the overlap matrix V between U(t) and U(t+∆t):
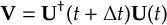 |
(8.133) |
For ∆t=0, clearly
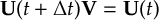 |
(8.134) |
and V can be identified with the phase matrix Φ.
For ∆t ≠ 0, we must now find a matrix P so that
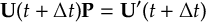 |
(8.135) |
still diagonalizes HMCH(t+∆t), but which minimizes the phase change with regard to U(t).
The matrix P has elements
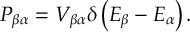 |
(8.136) |
where Eβ is the β-th eigenvalue of HMCH(t+∆t).
Within the SHARC algorithm, the phase of U(t+∆t) is adjusted to be most similar to U(t) by calculating first V, generating P from V and the eigenvalues of HMCH(t+∆t) and calculating the phase-corrected matrix U′(t+∆t) as U(t+∆t)P.
8.21.2 Tracking of the phase of the MCH wave functions
Additionally, within the quantum chemistry programs, the phases of the electronic wave functions may change from one time step to the next one. This will result in changes of the phase of all off-diagonal matrix elements (spin-orbit couplings, transition dipole moments, nonadiabatic couplings). SHARC has several possibilities to correct for that:
- The interface can provide wave function phases through QM.out.
- If the overlap matrix is available, its diagonal contains the necessary phase information.
- Otherwise the scalar products of old and new nonadiabatic couplings and the relative phase of SOC matrix elements can be used to construct phase information.
8.22 Random initial velocities
Random initial velocities are calculated with a given amount of kinetic energy E per atom a. For each atom, the velocity is calculated as follows, with two uniform random numbers θ and ϕ, from the interval [0,1[:
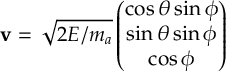 |
(8.137) |
This procedure gives a uniform probability distribution on a sphere with radius √{2E/ma}.
Note that the translational and rotational components of random initial velocities are not projected out in the current implementation.
Random initial velocities can be requested in the input with veloc random E, where E is a float defining the kinetic energy per atom (in eV).
8.23 Representations
Within SHARC, two different representations for the electronic states are used. The first is the so-called MCH basis, which is the basis of the eigenfunctions of the molecular Coulomb Hamiltonian. The molecular Coulomb Hamiltonian is the standard electronic Hamiltonian employed by the majority of quantum chemistry programs. It contains only the kinetic energy of the electrons and the potential energy arising from the Coulomb interaction between the electrons and nuclei.
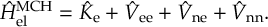 |
(8.138) |
With this hamiltonian, states of the same multiplicity couple via the nonadiabatic couplings, while states of different multiplicity do not interact at all.
The second representation used in SHARC is the so-called diagonal representation. It is the basis of the eigenfunctions of the total Hamiltonian.
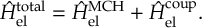 |
(8.139) |
The term ∧Helcoup contains additional couplings not contained in the molecular Coulomb Hamiltonian. The most common couplings are spin-orbit couplings and interactions with an external electric field.
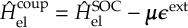 |
(8.140) |
Both of these couplings introduce off-diagonal elements in the total Hamiltonian. Thus, the eigenfunctions of the molecular Coulomb Hamiltonian are not the eigenfunctions of the total Hamiltonian.
Within SHARC, usually quantum chemistry information is read in the MCH representation, while the surface hopping is performed in the diagonal one.
8.23.1 Current state in MCH representation
Oftentimes, it is very useful to know to which MCH state the currently active diagonal state corresponds. If ∧Helcoup is small or the state separation is large, then each diagonal state approximately corresponds to one MCH state. Only in the case of large couplings and/or near-degenerate states are the MCH states strongly mixed in the diagonal states.
In order to obtain for a given time step from the currently active diagonal state β the corresponding MCH state α, a vector cdiag with cidiag=δiβ is generated. The vector is transformed into the MCH representation
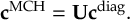 |
(8.141) |
The corresponding MCH state α is the index of the (absolute) largest element of vector cMCH.
8.24 Sampling from Wigner Distribution
The sampling is based on references [75,[76].
Besides the equilibrium geometry Req, the optimization plus frequency calculation provides a set of vibrational frequencies {νi} and the corresponding normal mode vectors {ni}, where i runs from 1 to N=3natom.
The normal mode vectors need to be provided in terms of mass-weighted Cartesian normal modes, in atomics units (Bohrs times square root of electron mass, i.e., a0·√{me}).
Most quantum chemistry programs follow different conventions when writing MOLDEN files. MOLPRO and MOLCAS write these files with unweighted Cartesian normal modes, with units of a0 (Bohrs). GAUSSIAN, TURBOMOLE, Q-CHEM, ADF, and ORCA employ what could be called the ” GAUSSIAN convention”, which are normalized Cartesian normal modes. COLUMBUS uses yet another convention in the output of their suscal.x module.
The script wigner.py automatically transforms these different conventions; it does so by applying all possible transformations to the input data until it finds one transformation which produces an orthonormal normal mode matrix.
The latter one is then used for the Wigner sampling.
In order to create an initial condition (R,v), the following procedure is applied. Initially, R0=Req and v0=0. Then, for each normal mode i, two random numbers Pi and Qi are chosen uniformly from the interval [−5,5]. The value of a ground state quantum Wigner distribution for these values is calculated:
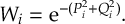 |
(8.142) |
Wi is compared to a uniform random ri number from [0,1]. If Wi > ri, then Pi and Qi are accepted.
Subsequently, the coordinates:
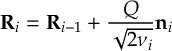 |
(8.143) |
and velocities
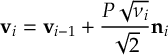 |
(8.144) |
are updated.
The random number procedure and updates are repeated for all normal modes, until (RN,v)N is obtained, which constitutes one initial condition. Finally, the center of mass is restored and translational and rotational components are projected out of v. The harmonic potential energy is given by:
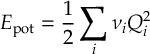 |
(8.145) |
8.24.1 Sampling at Non-zero Temperature
In the case of a non-zero temperature, the molecule might not be in the vibrational ground state of the harmonic oscillator, but rather in an excited vibrational state.
For a given mode i, the probability to be in any given vibrational state j (j=0 is the ground state) is:
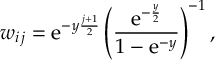 |
(8.146) |
where y is νi divided by kBT.
In order to find the vibrational state for mode i, a random number is drawn (from [0,1]) and used as in equation (8.152).
The displacements and velocity contributions for mode i in state j are then obtained as in equations (8.143) and (8.144), except that the Wigner distribution for state j is calculated as:
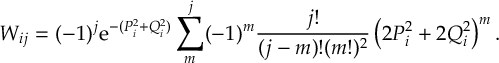 |
(8.147) |
8.25 Scaling
The scaling factor (keyword scaling) applies to all energies and derivatives of energies. Hence, the full Hamiltonian is scaled, and the gradients are scaled. Nothing else is scaled (no dipole moments, nonadiabatic couplings, overlaps, etc).
8.26 Seeding of the RNG
The standard Fortran 90 random number generator (used for sharc.x, but not for the auxiliary scripts) is seeded by a sequence of integers of length n, where n depends on the computer architecture. The input of SHARC, however, takes only a single RNG seed, which must reproducibly produce the same sequence of random numbers for the same input.
In order to generate the seed sequence from the single input x, the following procedure is applied:
- Query for the number n,
- Generate a first seed sequence s with si=x+37i+17i2,
- Seed with the sequence s,
- Obtain a sequence r of n random numbers on the interval [0,1[,
- Generate a second seed sequence s′ with si′=int(65536(ri−[1/2])),
- Reseed with the sequence s′.
The fifth step will generate a sequence of nearly uncorrelated numbers, distributed uniformly over the full range of possible integer values.
8.27 Selection of gradients and nonadiabatic couplings
In order to increase performance, it is possible to omit the calculation of certain gradients and nonadiabatic couplings. An energy-gap-based algorithm selects at each time step a subset of all possible gradients and nonadiabatic couplings to be calculated. Given the diagonal energy Ediagξ of the current active state ξ, the gradient gMCHα of MCH state α is calculated if:
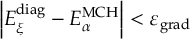 |
(8.148) |
where εgrad is the selection threshold.
Similarly, a nonadiabatic coupling vector KMCHβα is calculated if:
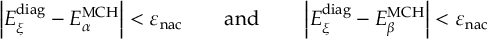 |
(8.149) |
with selection threshold εnac.
Neither gMCHα nor KMCHβα are ever calculated if α or β are frozen states.
There is only one keyword (eselect) to set the selection threshold, so εgrad and εnac are the same in most cases.
8.28 State ordering
The canonical ordering of MCH states of different S and MS in SHARC is as follows. In the innermost loop, the quantum number is increased; then MS and finally S. Example:
nstates 3 0 3
In this example, the order of states is given as:
| Number | Label | S | MS | n |
| 1 | S0 | 0 | 0 | 1 |
| 2 | S1 | 0 | 0 | 2 |
| 3 | S2 | 0 | 0 | 3 |
| 4 | T1− | 2 | -1 | 1 |
| 5 | T2− | 2 | -1 | 2 |
| 6 | T3− | 2 | -1 | 3 |
| 7 | T10 | 2 | 0 | 1 |
| 8 | T20 | 2 | 0 | 2 |
| 9 | T30 | 2 | 0 | 3 |
| 10 | T1+ | 2 | +1 | 1 |
| 11 | T2+ | 2 | +1 | 2 |
| 12 | T3+ | 2 | +1 | 3 |
The canonical ordering of states is for example important in order to specify the initial state in the MCH basis (using the state keyword in the input file).
Note that the diagonal states do not follow the same prescription. Since the diagonal states are in general not eigenfunctions of the total spin operator, they do not have a well-defined multiplicity.
Hence, the diagonal states are simply ordered by increasing energy.
8.29 Surface Hopping
Given two coefficient vectors cdiag(t) and cdiag(t+∆t) and the corresponding propagator matrix Rdiag(t+∆t,t), the surface hopping probabilities are given by
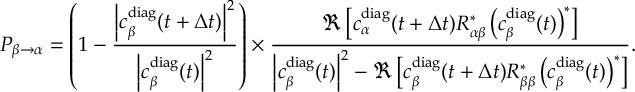 |
(8.150) |
where, however, Pβ→β=0 and all negative Pβ→α are set to zero.
This equation is the default in SHARC, and can be used with hopping_procedure sharc.
Alternatively, the hopping probabilities can be obtained with the “global flux surface hopping” method by Prezhdo and coworkers [71].
The equation is:
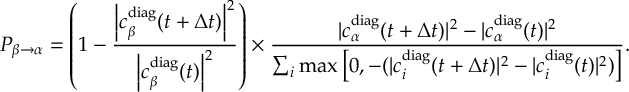 |
(8.151) |
As above, Pβ→β=0 and all negative Pβ→α are set to zero.
This equation and can be used with hopping_procedure gfsh.
In any case, the hopping procedure itself obtains a uniform random number r from the interval [0,1]. A hop to state α is performed, if
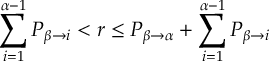 |
(8.152) |
See section 8.13.1 for further details on how frustrated hops (hops according to the hopping probabilities, but where not enough energy is available to execute the hop) are handled.
8.30 Self-Consistent Potential Methods
In trajectory surface hopping (TSH) methods, the trajectory is propagating on a single potential energy surface at each segment of time. Contrary, in the self-consistent potential (SCP) methods, trajectories are propagating on a SCP which is an äveraged” potential. The SCP methods are also self-consistent in terms of electronic and nuclear equations of motion (EOMs), and therefore, does not suffer from the notorious frustrated hops problem of TSH. The starting point of advanced SCP methods like CSDM is semiclassical Ehrenfest (SE), which is derivable from the time-dependent Schrödinger equation (TDSE).
Consider a wave function that is a product of electronic and nuclear wave functions
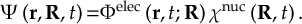 |
(8.153) |
Inserting the above molecular wave function into the TDSE, employing the independent trajectory approximation, and treating electrons as quantum particles by expanding the electronic wave function in a general basis (GB),
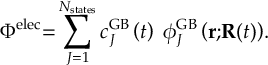 |
(8.154) |
With some mathematical manipulation, one obtains the equation of motion of generalized semiclassical Ehrenfest (GSE) dynamics. The electronic equation of motion of GSE is identical to that of surface hopping,
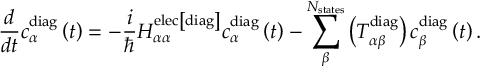 |
(8.155) |
Nuclear equation of motion involves two terms, namely, the adiabatic force and nonadiabatic force.
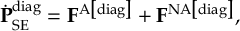 |
(8.156) |
where adiabatic force and nonadiabatic force are, respectively,
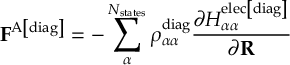 |
(8.157) |
and
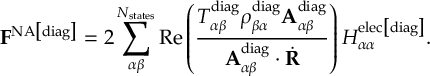 |
(8.158) |
The nonadiabatic force direction Aαβdiag can in principle be any direction that is not perpendicular to · R. Widely used choices of Aαβdiag are nonadiabatic coupling vector and effective nonadiabatic coupling vector.
8.31 Effective Nonadiabatic Coupling Vector
The effective nonadiabatic coupling vector Gαβ is a mixture of difference gradient vector and velocity vector.
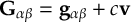 |
(8.159) |
where c is a coefficient. The coefficient c is determined by requiring that the dot product between effective nonadiabatic coupling vector and velocity vector equals time derivative coupling:
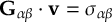 |
(8.160) |
8.32 Velocity Verlet
The nuclear coordinates of atom A are updated according to the Velocity Verlet algorithm [123], based on the gradient of state β at R(t) and R(t+∆t):
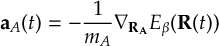 |
(8.161) |
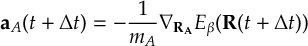 |
(8.162) |
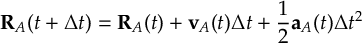 |
(8.163) |
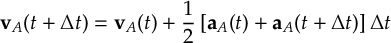 |
(8.164) |
Currently, there are no other integrators for the nuclear motion implemented in SHARC.
8.33 Wavefunction propagation
The electronic wave function is needed in order to carry out surface hopping. The electronic wave function is expanded in the basis of the so-called model space S, which includes the few lowest states |ψMCHα〉 of the multiplicities under consideration (e.g. the 3 lowest singlet and 2 lowest triplet states).
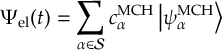 |
(8.165) |
All multiplet components are included explicitly, i.e., the inclusion of an MCH triplet state adds three explicit states to the model space (the three components of the triplet).
Within SHARC, the wave function is represented just by the vector cMCH. The Hamiltonian HMCH is represented in matrix form with elements:
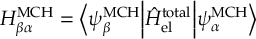 |
(8.166) |
From the MCH representation, the diagonal representation can be obtained by unitary transformation within the model space S (U†HMCHU=Hdiag and U†cMCH=cdiag):
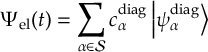 |
(8.167) |
and
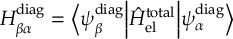 |
(8.168) |
The propagation of the electronic wave function from time t to t+∆t can then be written as the product of a propagation matrix with the coefficients at time t:
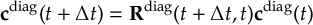 |
(8.169) |
or
 |
(8.170) |
In order to calculate RMCH(t+∆t,t), SHARC uses (unitary) operator exponentials.
8.33.1 Propagation using nonadiabatic couplings
Here we assume that in the dynamics the interaction between the electronic states is described by a matrix of nonadiabatic couplings KMCH(t), such that
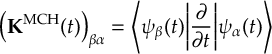 |
(8.171) |
or
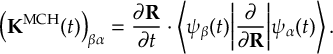 |
(8.172) |
In equation (8.171), the time-derivative couplings are directly calculated by the quantum chemistry program (use coupling ddt in the SHARC input), while in (8.172) the matrix KMCH(t) is obtained from the scalar product of the nuclear velocity and the nonadiabatic coupling vectors (use coupling ddr in the input).
The propagation matrix can then be written as
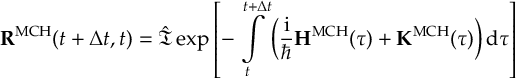 |
(8.173) |
with the time-ordering operator ∧T. For small time steps ∆t, HMCH(τ) and KMCH(τ) can be interpolated linearly
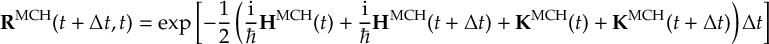 |
(8.174) |
And in order to have a sufficiently small time step for this to work, the interval (t,t+∆t) is further split into subtime steps ∆τ = [(∆t)/n].
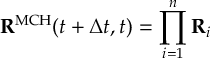 |
(8.175) |
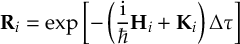 |
(8.176) |
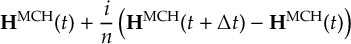 |
(8.177) |
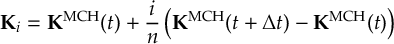 |
(8.178) |
8.33.2 Propagation using overlap matrices – Local diabatization
In many situations, the nonadiabatic couplings in KMCH are very localized on the potential hypersurfaces. If this is the case, in the dynamics very short time steps are necessary to properly sample the nonadiabatic couplings. If too large time steps are used, part of the coupling may be missed, leading to wrong population transfer. The local diabatization algorithm gives more numerical stability in these situations. It can be requested with the line coupling overlap in the input file.
Within this algorithm, the change of the electronic states between time steps is described by the overlap matrix SMCH(t,t+∆t)
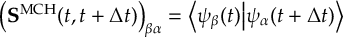 |
(8.179) |
With this, the propagator matrix can be written as
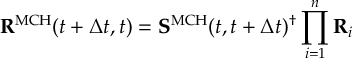 |
(8.180) |
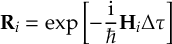 |
(8.181) |
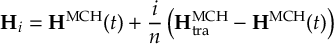 |
(8.182) |
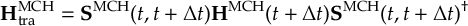 |
(8.183) |
8.33.3 Propagation using overlap matrices – Norm-preserving interpolation
Alternatively, one can use accurate interpolation of time derivative coupling from overlap matrices. Propagating the coefficients can be written as,
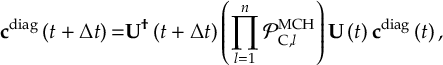 |
(8.184) |
where n is the number of substeps (which can be set up by keyword nsubsteps), and l is the index of substep, with substep propagator PMCHC,l defined as,
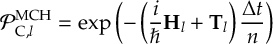 |
(8.185) |
where,
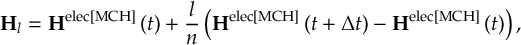 |
(8.186) |
i.e., one linearly interpolates the MCH Hamiltonian Helec[MCH] between time t and t+∆t.
In SHARC3.0, the Tl has variants definitions, and these variants define most of the options available in SHARC3.0 keyword eeom. One can have the following possible definitions:
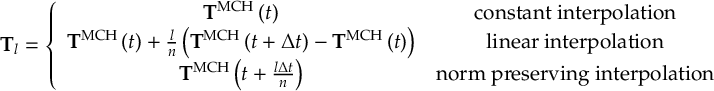 |
(8.187) |
where TMCH(t+[(l∆t)/n]) is the TDC at time t+[(l∆t)/n] which is not computed from electronic structure software, but instead it is from a norm preserving interpolation [115]. During time t and t+∆t, TDC at time T writes
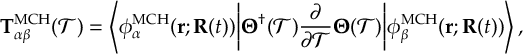 |
(8.188) |
where Θ(T) is a time-dependent transformation matrix that interpolates the MCH (adiabatic) electronic wave functions between time t and t+∆t:
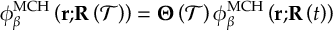 |
(8.189) |
with
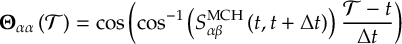 |
(8.190) |
and
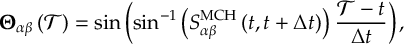 |
(8.191) |
where SMCHαβ is the overlap integral defined in equation equation (8.179).
8.34 Evaluation of Time Derivative Couplings and Curvature Approximation
One of the key ingredients in propagating electronic and nuclear EOMs for GSE and electronic EOM for TSH is time derivative couoling (TDC) in MCH representation. And TDC serves the role as the electronic interstate coupling in the nonadiabatic dynamics. Because TDC cannot be computed directly from electronic structure software, TDC is evaluated by postprocessing quantum chemistry data. There are three ways to compute TDC: NAC-based, overlap-based, and curvature-driven. These three ways of computing TDC corresponds to the three types of algorithms respectively. And controlling the method of TDC evaluation in SHARC3.0 is done by using keyword coupling.
NAC-based TDC
The NAC-based TDC is computed according to equation (8.172), which means a requirement of computing NACs dMCH in MCH representation from quantum chemistry software. Notice that dMCH computational cost scales quadratically as the number of electronic states involved. Therefore it is expensive. In addition, it limits the choices of electronic structure theory, because there is only very limited number of electronic structure theories for which the analytical implementation of NAC is available. Using NAC-based algorithm is enabled by using keyword coupling nacdr or coupling ddr.
Overlap-based TDC
There are three ways to compute overlap-based TDC, all based on overlap integrals defined in equation (8.179).
Therefore, to compute overlap-based TDC, one needs to compute electronic wave functions but not NACs from quantum chemistry software. Tully and Hammes-Schiffer first recognized that TDC can be evaluated based on overlaps. And this is called the Hammes-Schiffer-Tully (HST) scheme of evaluation of TDC from overlaps:
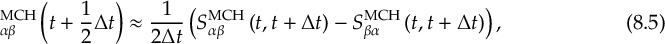 |
(8.192) |
where t is time, and ∆t is the time step. The HST scheme is improved by considering high-order finite difference:
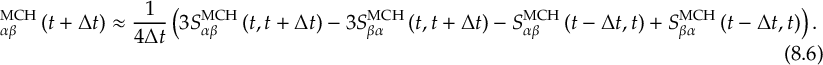 |
(8.193) |
And TDC is most accurately evaluated by a norm-preserving interpolation (NPI) scheme
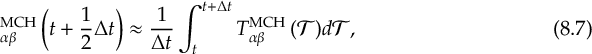 |
(8.194) |
where TMCHαβ(T) is defined in equation (8.189).
The current implementation of SHARC3.0 employs the NPI scheme to compute overlap-based TDC. However, how TDC is actually used in propagation of electronic EOM is controlled by the keyword eeom and is discussed in section 8.33.
One of the advantages of using NPI scheme over HST or high-order finite difference scheme is that it is more accurate for a situation where the nonadiabatic coupling vector is narrowly peaked (note that NAC is related to TDC), which is often called trivial crossings. It is also more accurate in propagating electronic EOM compared to NAC-based algorithms.
Also notice that the subtle difference between an NPI scheme to evaluate TDCs and the NPI algorithm to propagate electronic EOM. These two are closely related but different.
Using an overlap-based algorithm is enabled by using keyword coupling overlap.
Curvature-driven TDC
The curvature-driven TDC is an approximated TDC that is evaluated from the curvature of potential energy surfaces. Therefore, to compute curvature-driven TDC, one only needs to compute potential energies, neither electronic wave functions nor NACs/overlaps are need from quantum chemistry software. As pointed out by Baeck and An, NAC in a one-dimensional system can be approximated by
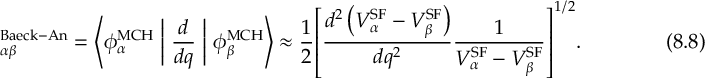 |
(8.195) |
For simplicity we have defined
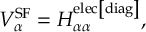 |
(8.196) |
where q is a one-dimensional nuclear coordinate, and we have also adapted the original Baeck and An NAC to the current notation, i.e., the original Baeck and An NAC was considering only for internal conversion processes.
We recognized that a trajectory is in fact propagating on a one-dimensional coordinate which is time. Combining this observation with Baeck and An one-dimensional approximation of NAC gives the definition of curvature-driven TDC (\kappaupTDC)
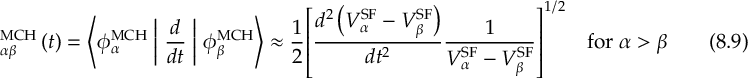 |
(8.197) |
with
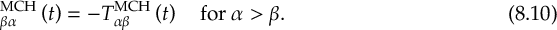 |
(8.198) |
Evaluation of the curvature of potential energy with respective to time can be done in two ways, namely by computing first-order differentiation of the time derivative of potential energies from backward finite difference (which is called gradient method), or second-order time derivative of potential energies from backward finite difference (which is called energy method).
We first discuss the gradient method. The gradient method is controlled by using keyword ktdc_method gradient. In thte gradient method, we employ the chain rule
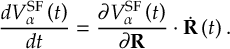 |
(8.199) |
Therefore, (8.197) can be written as
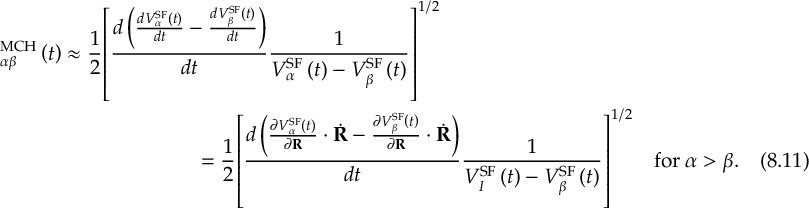 |
(8.200) |
If we define
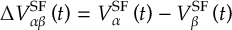 |
(8.201) |
and
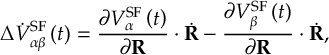 |
(8.202) |
then Equation (8.200) is approximated by backward finite difference as
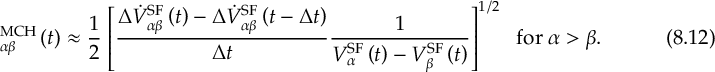 |
(8.203) |
Equations (8.202) and (8.203) define the gradient method. We can see that gradient method requires computation of gradients of all electronic states.
Next we discuss the energy method. The energy method is controlled by using keyword ktdc_method energy. In the energy method, we compute the curvature of potential energy with respective to time directly by backward finite difference as
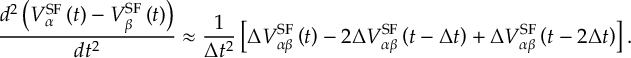 |
(8.204) |
Starting from the fourth step, we can use
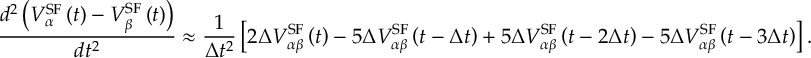 |
(8.205) |
Which method is more practical depends on the details of the simulation.
For TSH without SOCs, only one gradient is needed per time step.
Hence, the gradient method-which requires all gradients-adds significant extra cost and thus for TSH without SOCs it is more convenient to use the energy method.
For TSH with SOCs (and without gradient selection) or for SCP, all gradients are computed anyways, so using the gradient method does not add extra cost.
Thus, the more accurate gradient method is recommended in these cases.
Using the curvature-driven algorithm is enabled by using keyword coupling ktdc. And one can optionally use keyword ktdc_method to select either gradient or energy method to compute \kappaupTDC. Otherwise, the default options for TSH is ktdc_method energy, and for SCP is ktdc_method gradient.
Chapter 9
Bibliography
Bibliography
- [1]
-
M. Kasha:
“”Characterization of
electronic transitions in complex molecules. Discuss. Faraday Soc.,
9, 14 (1950). - [2]
-
C. M. Marian: “”Spin-orbit
coupling and intersystem crossing in molecules. WIREs Comput. Mol.
Sci., 2, 187-203 (2012). - [3]
-
I. Wilkinson, A. E. Boguslavskiy, J. Mikosch, D. M. Villeneuve, H.-J. Wörner,
M. Spanner, S. Patchkovskii, A. Stolow:
“”Non-adiabatic and
intersystem crossing dynamics in SO2 I: Bound State Relaxation Studied
By Time-Resolved Photoelectron Photoion Coincidence Spectroscopy. J.
Chem. Phys., 140, 204 301 (2014). - [4]
-
S. Mai, P. Marquetand, L. González:
“”Non-Adiabatic Dynamics in
SO2: II. The Role of Triplet States Studied by Surface-Hopping
Simulations. J. Chem. Phys., 140, 204 302 (2014). - [5]
-
C. Lévêque, R. Taïeb, H. Köppel:
“”Communication:
Theoretical prediction of the importance of the 3B2 state in the
dynamics of sulfur dioxide. J. Chem. Phys., 140, 091101
(2014). - [6]
-
T. J. Penfold, R. Spesyvtsev, O. M. Kirkby, R. S. Minns, D. S. N. Parker, H. H.
Fielding, G. A. Worth:
“”Quantum dynamics study of
the competing ultrafast intersystem crossing and internal conversion in the
“channel 3” region of benzene. J. Chem. Phys., 137,
204310 (2012). - [7]
-
R. A. Vogt, C. Reichardt, C. E. Crespo-Hernández:
“”Excited-State Dynamics in
Nitro-Naphthalene Derivatives: Intersystem Crossing to the Triplet Manifold
in Hundreds of Femtoseconds. J. Phys. Chem., 117,
6580-6588 (2013). - [8]
-
C. E. Crespo-Hernández, B. Cohen, P. M. Hare, B. Kohler:
“”Ultrafast Excited-State
Dynamics in Nucleic Acids. Chem. Rev., 104, 1977-2020
(2004). - [9]
-
M. Richter, P. Marquetand, J. González-Vázquez, I. Sola, L. González:
“”Femtosecond Intersystem
Crossing in the DNA Nucleobase Cytosine. J. Phys. Chem. Lett.,
3, 3090-3095 (2012). - [10]
-
L. Martínez-Fernández, L. González, I. Corral:
“”An Ab Initio Mechanism
for Efficient Population of Triplet States in Cytotoxic Sulfur Substituted
DNA Bases: The Case of 6-Thioguanine. Chem. Commun., 48,
2134-2136 (2012). - [11]
-
S. Mai, P. Marquetand, M. Richter, J. González-Vázquez, L. González:
“”Singlet and Triplet
Excited-State Dynamics Study of the Keto and Enol Tautomers of Cytosine.
ChemPhysChem, 14, 2920-2931 (2013). - [12]
-
C. Reichardt, C. E. Crespo-Hernández:
“”Ultrafast Spin Crossover
in 4-Thiothymidine in an Ionic Liquid. Chem. Commun., 46,
5963-5965 (2010). - [13]
-
J. C. Tully, R. K. Preston:
“”Trajectory Surface
Hopping Approach to Nonadiabatic Molecular Collisions: The Reaction of
H+ with D2. J. Chem. Phys., 55, 562-572 (1971). - [14]
-
J. C. Tully: “”Molecular
dynamics with electronic transitions. J. Chem. Phys., 93,
1061-1071 (1990). - [15]
-
M. Barbatti: “”Nonadiabatic
dynamics with trajectory surface hopping method. WIREs Comput. Mol.
Sci., 1, 620-633 (2011). - [16]
-
J. E. Subotnik, A. Jain, B. Landry, A. Petit, W. Ouyang, N. Bellonzi:
“”Understanding
the Surface Hopping View of Electronic Transitions and Decoherence.
Annu. Rev. Phys. Chem., 67, 387-417 (2016). - [17]
-
L. Wang, A. Akimov, O. V. Prezhdo:
“”Recent Progress
in Surface Hopping: 2011–2015. J. Phys. Chem. Lett., 7,
2100-2112 (2016). - [18]
-
N. L. Doltsinis: “”Molecular Dynamics Beyond the Born-Oppenheimer
Approximation: Mixed Quantum-Classical Approaches. In J. Grotendorst,
S. Blügel, D. Marx (editors), Computational Nanoscience: Do It
Yourself!, volume 31 of NIC Series, 389-409, John von Neuman
Institut for Computing, Jülich (2006). - [19]
-
N. L. Doltsinis, D. Marx:
“”First Principles
Molecular Dynamics Involving Excited States And Nonadiabatic Transitions.
J. Theor. Comput. Chem., 1, 319-349 (2002). - [20]
-
S. Hammes-Schiffer, J. C. Tully:
“”Proton transfer in
solution: Molecular dynamics with quantum transitions. J. Chem.
Phys., 101, 4657-4667 (1994). - [21]
-
G. Granucci, M. Persico:
“”Critical appraisal of the
fewest switches algorithm for surface hopping. J. Chem. Phys.,
126, 134 114 (2007). - [22]
-
M. Thachuk, M. Y. Ivanov, D. M. Wardlaw:
“”A semiclassical approach
to intense-field above-threshold dissociation in the long wavelength limit.
J. Chem. Phys., 105, 4094-4104 (1996). - [23]
-
B. Maiti, G. C. Schatz, G. Lendvay:
“”Importance of Intersystem
Crossing in the S(3P, 1D) + H2 → SH + H Reaction. J.
Phys. Chem. A, 108, 8772-8781 (2004). - [24]
-
G. A. Jones, A. Acocella, F. Zerbetto:
“”On-the-Fly,
Electric-Field-Driven, Coupled Electron-Nuclear Dynamics. J. Phys.
Chem. A, 112, 9650-9656 (2008). - [25]
-
R. Mitri\’c, J. Petersen, V. Bonac\’c-Koutecký:
“”Laser-field-induced
surface-hopping method for the simulation and control of ultrafast
photodynamics. Phys. Rev. A, 79, 053 416 (2009). - [26]
-
G. Granucci, M. Persico, G. Spighi:
“”Surface hopping
trajectory simulations with spin-orbit and dynamical couplings. J.
Chem. Phys., 137, 22A501 (2012). - [27]
-
B. F. E. Curchod, T. J. Penfold, U. Rothlisberger, I. Tavernelli:
“”Local Control
Theory using Trajectory Surface Hopping and Linear-Response Time-Dependent
Density Functional Theory. Chimia, 67, 218-221 (2013). - [28]
-
G. Cui, W. Thiel:
“”Generalized trajectory
surface-hopping method for internal conversion and intersystem crossing.
J. Chem. Phys., 141, 124 101 (2014). - [29]
-
J. Pittner, H. Lischka, M. Barbatti:
“”Optimization
of mixed quantum-classical dynamics: Time-derivative coupling terms and
selected couplings. Chem. Phys., 356, 147 – 152 (2009). - [30]
-
A. Jain, E. Alguire, J. E. Subotnik:
“”An Efficient,
Augmented Surface Hopping Algorithm That Includes Decoherence for Use in
Large-Scale Simulations. J. Chem. Theory Comput., 12,
5256-5268 (2016). - [31]
-
M. Ruckenbauer, S. Mai, P. Marquetand, L. González:
“”Revealing Deactivation
Pathways Hidden in Time-Resolved Photoelectron Spectra. Sci. Rep.,
6, 35 522 (2016). - [32]
-
F. Plasser, M. Wormit, A. Dreuw:
“”New tools for the
systematic analysis and visualization of electronic excitations. I.
Formalism. J. Chem. Phys., 141, 024 106 (2014). - [33]
-
F. Plasser, S. A. Bäppler, M. Wormit, A. Dreuw:
“”New tools for the
systematic analysis and visualization of electronic excitations. II.
Applications. J. Chem. Phys., 141, 024 107 (2014). - [34]
-
F. Plasser: “”TheoDORE: A package for theoretical density, orbital
relaxation, and exciton analysis. http://theodore-qc.sourceforge.net (2017). - [35]
-
B. R. Landry, M. J. Falk, J. E. Subotnik:
“”Communication: The
correct interpretation of surface hopping trajectories: How to calculate
electronic properties. J. Chem. Phys., 139, 211 101
(2013). - [36]
-
S. Mai, P. Marquetand, L. González:
“”Nonadiabatic dynamics:
The SHARC approach. WIREs Comput. Mol. Sci., 8, e1370
(2018). - [37]
-
S. Mai, D. Avagliano, M. Heindl, P. Marquetand, M. F. S. J. Menger, M. Oppel,
F. Plasser, S. Polonius, M. Ruckenbauer, Y. Shu, D. G. Truhlar, L. Zhang,
P. Zobel, L. González: “”SHARC3.0: Surface Hopping Including
Arbitrary Couplings – Program Package for Non-Adiabatic Dynamics.
https://sharc-md.org/ (2023). - [38]
-
M. Richter, P. Marquetand, J. González-Vázquez, I. Sola, L. González:
“”SHARC: Ab Initio
Molecular Dynamics with Surface Hopping in the Adiabatic Representation
Including Arbitrary Couplings. J. Chem. Theory Comput., 7,
1253-1258 (2011). - [39]
-
M. Richter, P. Marquetand, J. González-Vázquez, I. Sola, L. González:
“”Correction to SHARC: Ab
Initio Molecular Dynamics with Surface Hopping in the Adiabatic
Representation Including Arbitrary Couplings. J. Chem. Theory
Comput., 8, 374-374 (2012). - [40]
-
J. J. Bajo, J. González-Vázquez, I. Sola, J. Santamaria, M. Richter,
P. Marquetand, L. González:
“”Mixed Quantum-Classical
Dynamics in the Adiabatic Representation to Simulate Molecules Driven by
Strong Laser Pulses. J. Phys. Chem. A, 116, 2800-2807
(2012). - [41]
-
P. Marquetand, M. Richter, J. González-Vázquez, I. Sola, L. González:
“”Nonadiabatic ab initio
molecular dynamics including spin-orbit coupling and laser fields.
Faraday Discuss., 153, 261-273 (2011). - [42]
-
S. Mai, P. Marquetand, L. González:
“”A General Method to
Describe Intersystem Crossing Dynamics in Trajectory Surface Hopping.
Int. J. Quantum Chem., 115, 1215-1231 (2015). - [43]
-
S. Mai, F. Plasser, P. Marquetand, L. González:
“”General
trajectory surface hopping method for ultrafast nonadiabatic dynamics. In
M. Vrakking, F. Lepine (editors), Attosecond Molecular Dynamics,
chapter 10, 348-385, The Royal Society of Chemistry (2018). - [44]
-
S. Mai, M. Richter, P. Marquetand, L. González:
“”Excitation of
Nucleobases from a Computational Perspective II: Dynamics. In
M. Barbatti, A. C. Borin, S. Ullrich (editors), Photoinduced Phenomena
in Nucleic Acids I, volume 355 of Topics in Current Chemistry,
99-153, Springer Berlin Heidelberg (2015). - [45]
-
L. González, P. Marquetand, M. Richter, J. González-Vázquez, I. Sola:
“”Ultrafast
laser-induced processes described by ab initio molecular dynamics. In
R. de Nalda, L. Bañares (editors), Ultrafast Phenomena in Molecular
Sciences, volume 107 of Springer Series in Chemical Physics,
145-170, Springer (2014). - [46]
-
M. Richter, S. Mai, P. Marquetand, L. González:
“”Ultrafast Intersystem
Crossing Dynamics in Uracil Unravelled by Ab Initio Molecular Dynamics.
Phys. Chem. Chem. Phys., 16, 24 423-24 436 (2014). - [47]
-
L. Martínez-Fernández, J. González-Vázquez, L. González,
I. Corral: “”Time-resolved
insight into the photosensitized generation of singlet oxygen in
endoperoxides. J. Chem. Theory Comput., accepted (2014). - [48]
-
M. E. Corrales, V. Loriot, G. Balerdi, J. González-Vázquez,
R. de Nalda, L. Bañares, A. H. Zewail:
“”Structural dynamics
effects on the ultrafast chemical bond cleavage of a photodissociation
reaction. Phys. Chem. Chem. Phys., 16, 8812-8818 (2014). - [49]
-
C. E. Crespo-Hernández, L. Martínez-Fernández, C. Rauer, C. Reichardt,
S. Mai, M. Pollum, P. Marquetand, L. González, I. Corral:
“”Electronic and Structural
Elements That Regulate the Excited-State Dynamics in Purine Nucleobase
Derivatives. J. Am. Chem. Soc., 137, 4368-4381 (2015). - [50]
-
M. Marazzi, S. Mai, D. Roca-Sanjuán, M. G. Delcey, R. Lindh, L. González,
A. Monari:
“”Benzophenone
Ultrafast Triplet Population: Revisiting the Kinetic Model by Surface-Hopping
Dynamics. J. Phys. Chem. Lett., 7, 622-626 (2016). - [51]
-
M. Richter, B. P. Fingerhut:
“”Simulation of
Multi-Dimensional Signals in the Optical Domain: Quantum-Classical Feedback
in Nonlinear Exciton Propagation. J. Chem. Theory Comput.,
12, 3284-3294 (2016). - [52]
-
J. Cao, Z.-Z. Xie, X. Yu:
“”Excited-state
dynamics of oxazole: A combined electronic structure calculations and dynamic
simulations study. Chem. Phys., 474, 25 – 35 (2016). - [53]
-
A. Banerjee, D. Halder, G. Ganguly, A. Paul:
“”Deciphering the cryptic
role of a catalytic electron in a photochemical bond dissociation using
excited state aromaticity markers. Phys. Chem. Chem. Phys.,
18, 25 308-25 314 (2016). - [54]
-
S. Mai, P. Marquetand, L. González:
“”Intersystem
Crossing Pathways in the Noncanonical Nucleobase 2-Thiouracil: A
Time-Dependent Picture. J. Phys. Chem. Lett., 7, 1978-1983
(2016). - [55]
-
S. Mai, M. Pollum, L. Martínez-Fernández, N. Dunn, P. Marquetand,
I. Corral, C. E. Crespo-Hernández, L. González:
“”The Origin of Efficient
Triplet State Population in Sulfur-Substituted Nucleobases. Nat.
Commun., 7, 13 077 (2016). - [56]
-
F. Peccati, S. Mai, L. González:
“”Insights into the
Deactivation of 5-Bromouracil after UV Excitation. Phil. Trans. R.
Soc. A, 375, 20160 202 (2017). - [57]
-
M. Murillo-Sánchez, S. M. Poullain, J. González-Vázquez, M. Corrales,
G. Balerdi, L. Bañares:
“”Femtosecond
photodissociation dynamics of chloroiodomethane in the first absorption
band. Chem. Phys. Lett., 683, 22 – 28 (2017), ahmed Zewail
(1946-2016) Commemoration Issue of Chemical Physics Letters. - [58]
-
A. C. Borin, S. Mai, P. Marquetand, L. González:
“”Ab initio molecular
dynamics relaxation and intersystem crossing mechanisms of 5-azacytosine.
Phys. Chem. Chem. Phys., 19, 5888-5894 (2017). - [59]
-
S. Mai, M. Richter, P. Marquetand, L. González:
“”The DNA
Nucleobase Thymine in Motion – Intersystem Crossing Simulated with Surface
Hopping. Chem. Phys., 482, 9-15 (2017). - [60]
-
F. M. Siouri, S. Boldissar, J. A. Berenbeim, M. S. de Vries:
“”Excited State
Dynamics of 6-Thioguanine. J. Phys. Chem. A, 121,
5257-5266 (2017). - [61]
-
D. Bellshaw, D. A. Horke, A. D. Smith, H. M. Watts, E. Jager, E. Springate,
O. Alexander, C. Cacho, R. T. Chapman, A. Kirrander, R. S. Minns:
“”Ab-initio
surface hopping and multiphoton ionisation study of the photodissociation
dynamics of CS2. Chem. Phys. Lett., 683, 383-388 (2017). - [62]
-
S. Sun, B. Mignolet, L. Fan, W. Li, R. D. Levine, F. Remacle:
“”Nuclear Motion
Driven Ultrafast Photodissociative Charge Transfer of the PENNA Cation: An
Experimental and Computational Study. J. Phys. Chem. A,
121, 1442-1447 (2017). - [63]
-
C. Rauer, J. J. Nogueira, P. Marquetand, L. González:
“”Cyclobutane Thymine
Photodimerization Mechanism Revealed by Nonadiabatic Molecular Dynamics.
J. Am. Chem. Soc., 138, 15 911-15 916 (2016). - [64]
-
A. J. Atkins, L. González:
“”Trajectory
Surface-Hopping Dynamics Including Intersystem Crossing in
[Ru(bpy)3]2+. J. Phys. Chem. Lett., 8, 3840-3845
(2017). - [65]
-
T. Schnappinger, P. Kolle, M. Marazzi, A. Monari, L. González,
R. de Vivie-Riedle: “”Ab
initio molecular dynamics of thiophene: the interplay of internal conversion
and intersystem crossing. Phys. Chem. Chem. Phys., 19,
25 662-25 670 (2017). - [66]
-
S. Mai, F. Plasser, M. Pabst, F. Neese, A. Köhn, L. González:
“”Surface Hopping Dynamics
Including Intersystem Crossing using the Algebraic Diagrammatic Construction
Method. J. Chem. Phys., 147, 184 109 (2017). - [67]
-
J. P. Zobel, J. J. Nogueira, L. González:
“”The Mechanism of
Ultrafast Intersystem Crossing in 2-Nitronaphthalene. Chem. Eur. J.,
DOI:10.1002/chem.201705854 (2018). - [68]
-
C. Rauer, J. J. Nogueira, P. Marquetand, L. González:
“”Stepwise
photosensitized thymine dimerization mediated by an exciton intermediate.
Monatsh. Chem., 149, 1-9 (2018). - [69]
-
J. Cao:
“”The
position of the N atom in the pentacyclic ring of heterocyclic molecules
affects the excited-state decay: A case study of isothiazole and thiazole.
J. Mol. Struct., DOI:10.1016/j.molstruc.2017.11.008 (2018). - [70]
-
R. J. Squibb, M. Sapunar, A. Ponzi, R. Richter, A. Kivimäki, O. Plekan,
P. Finetti, N. Sisourat, V. Zhaunerchyk, T. Marchenko, L. Journel,
R. Guillemin, R. Cucini, M. Coreno, C. Grazioli, M. Di Fraia, C. Callegari,
K. C. Prince, P. Decleva, M. Simon, J. H. D. Eland, N. Dosli\’c,
R. Feifel, M. N. Piancastelli:
“”Acetylacetone
photodynamics at a seeded free-electron laser. Nat. Commun.,
9, 63 (2018). - [71]
-
L. Wang, D. Trivedi, O. V. Prezhdo:
“”Global Flux Surface
Hopping Approach for Mixed Quantum-Classical Dynamics. J. Chem.
Theory Comput., 10, 3598-3605 (2014). - [72]
-
G. Granucci, M. Persico, A. Toniolo:
“”Direct Semiclassical
Simulation of Photochemical Processes with Semiempirical Wave Functions.
J. Chem. Phys., 114, 10 608-10 615 (2001). - [73]
-
F. Plasser, G. Granucci, J. Pittner, M. Barbatti, M. Persico, H. Lischka:
“”Surface Hopping Dynamics
using a Locally Diabatic Formalism: Charge Transfer in The Ethylene Dimer
Cation and Excited State Dynamics in the 2-Pyridone Dimer. J. Chem.
Phys., 137, 22A514 (2012). - [74]
-
F. Plasser, M. Ruckenbauer, S. Mai, M. Oppel, P. Marquetand, L. González:
“”Efficient and
Flexible Computation of Many-Electron Wave Function Overlaps. J.
Chem. Theory Comput., 12, 1207 (2016). - [75]
-
J. P. Dahl, M. Springborg:
“”The Morse oscillator
in position space, momentum space, and phase space. J. Chem. Phys.,
88, 4535-4547 (1988). - [76]
-
R. Schinke: Photodissociation Dynamics: Spectroscopy and Fragmentation of
Small Polyatomic Molecules. Cambridge University Press (1995). - [77]
-
M. Barbatti, K. Sen:
“”Effects of different
initial condition samplings on photodynamics and spectrum of pyrrole.
Int. J. Quantum Chem., 116, 762-771 (2016). - [78]
-
M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar,
M. Eckert-Maksi\’c, H. Lischka:
“”The
on-the-fly surface-hopping program system Newton-X: Application to ab
initio simulation of the nonadiabatic photodynamics of benchmark systems.
J. Photochem. Photobiol. A, 190, 228-240 (2007). - [79]
-
D. Cremer, J. A. Pople:
“”General definition of
ring puckering coordinates. J. Am. Chem. Soc., 97,
1354-1358 (1975). - [80]
-
J. C. A. Boeyens: “”The
conformation of six-membered rings. J. Cryst. Mol. Struct.,
8, 317 (1978). - [81]
-
L. Kurtz, A. Hofmann, R. de Vivie-Riedle:
“”Ground state normal mode
analysis: Linking excited state dynamics and experimental observables.
J. Chem. Phys., 114, 6151-6159 (2001). - [82]
-
F. Plasser: Dynamics Simulation of Excited State Intramolecular Proton
Transfer. Master’s thesis, University of Vienna (2009). - [83]
-
A. Amadei, A. B. M. Linssen, H. J. C. Berendsen:
“”Essential dynamics
of proteins. Proteins: Struct., Funct., Bioinf., 17,
412-425 (1993). - [84]
-
S. Nangia, A. W. Jasper, T. F. Miller, D. G. Truhlar:
“”Army Ants Algorithm for
Rare Event Sampling of Delocalized Nonadiabatic Transitions by Trajectory
Surface Hopping and the Estimation of Sampling Errors by the Bootstrap
Method. J. Chem. Phys., 120, 3586-3597 (2004). - [85]
-
M. J. Bearpark, M. A. Robb, H. B. Schlegel:
“”A direct
method for the location of the lowest energy point on a potential surface
crossing. Chem. Phys. Lett., 223, 269 (1994). - [86]
-
B. G. Levine, J. D. Coe, T. J. Martínez:
“”Optimizing Conical
Intersections without Derivative Coupling Vectors: Application to Multistate
Multireference Second-Order Perturbation Theory (MS-CASPT2). J.
Phys. Chem. B, 112, 405-413 (2008). - [87]
-
M. Ruckenbauer, S. Mai, P. Marquetand, L. González:
“”Photoelectron spectra of
2-thiouracil, 4-thiouracil, and 2,4-dithiouracil. J. Chem. Phys.,
144, 074 303 (2016). - [88]
-
F. Plasser, L. González:
“”Communication:
Unambiguous comparison of many-electron wavefunctions through their
overlaps. J. Chem. Phys., 145, 021 103 (2016). - [89]
-
F. Plasser, S. Goméz, S. Mai, L. González:
“”Highly efficient surface
hopping dynamics using a linear vibronic coupling model. Phys. Chem.
Chem. Phys., Advance Article, DOI:10.1039/C8CP05 662E (2018). - [90]
-
J. Westermayr, M. Gastegger, P. Marquetand:
“”Combining
SchNet and SHARC: The SchNarc Machine Learning Approach for Excited-State
Dynamics. J. Phys. Chem. Lett., 11, 3828-3834 (2020). - [91]
-
C. Zhu, S. Nangia, A. W. Jasper, D. G. Truhlar:
“”Coherent switching with
decay of mixing: An improved treatment of electronic coherence for
non-Born-Oppenheimer trajectories. J. Chem. Phys., 121,
7658-7670 (2004). - [92]
-
Y. Shu, L. Zhang, S. Mai, S. Sun, L. González, D. G. Truhlar:
“”Implementation of
Coherent Switching with Decay of Mixing into the SHARC Program. J.
Chem. Theory Comput., 16, 3464-3475 (2020). - [93]
-
Y. Shu, L. Zhang, S. Sun, D. G. Truhlar:
“”Time-Derivative
Couplings for Self-Consistent Electronically Nonadiabatic Dynamics.
J. Chem. Theory Comput., 16, 4098-4106 (2020). - [94]
-
Y. Shu, D. G. Truhlar:
“”Decoherence and
Its Role in Electronically Nonadiabatic Dynamics. J. Chem. Theory
Comput. (2023). - [95]
-
Y. Shu, L. Zhang, Z. Varga, K. A. Parker, S. Kanchanakungwankul, S. Sun, D. G.
Truhlar:
“”Conservation of
Angular Momentum in Direct Nonadiabatic Dynamics. J. Phys. Chem.
Lett., 11, 1135-1140 (2020). - [96]
-
Y. Shu, L. Zhang, D. Wu, X. Chen, S. Sun, D. G. Truhlar: “”New Gradient
Correction Scheme for Electronically Nonadiabatic Dynamics Involving Multiple
Spin States. J. Chem. Theory Comput. (2023). - [97]
-
A. W. Jasper, S. N. Stechmann, D. G. Truhlar:
“”Fewest-switches with time
uncertainty: A modified trajectory surface-hopping algorithm with better
accuracy for classically forbidden electronic transitions. J. Chem.
Phys., 116, 5424-5431 (2002). - [98]
-
X. Zhao, Y. Shu, L. Zhang, X. Xu, D. G. Truhlar:
“”Direct
Nonadiabatic Dynamics of Ammonia with Curvature-Driven Coherent Switching
with Decay of Mixing and with Fewest Switches with Time Uncertainty: An
Illustration of Population Leaking in Trajectory Surface Hopping Due to
Frustrated Hops. J. Chem. Theory Comput., 19, 1672-1685
(2023). - [99]
-
H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz:
“”Molpro: A general-purpose
quantum chemistry program package. WIREs Comput. Mol. Sci.,
2, 242-253 (2012). - [100]
-
H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, et al.: “”MOLPRO,
version 2012.1, a package of ab initio programs. www.molpro.net (2012). - [101]
-
G. Karlström, R. Lindh, P.- Å. Malmqvist, B. O. Roos, U. Ryde,
V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady,
L. Seijo:
“”MOLCAS: a
program package for computational chemistry. Comput. Mater. Sci.,
28, 222 – 239 (2003). - [102]
-
F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P.- Å. Malmqvist,
P. Neogrády, T. B. Pedersen, M. Pitonák, M. Reiher, B. O. Roos,
L. Serrano-Andrés, M. Urban, V. Veryazov, R. Lindh:
“”MOLCAS 7: The Next
Generation. J. Comput. Chem., 31, 224-247 (2010). - [103]
-
F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey,
L. De Vico, I. Fdez. Galván, N. Ferré, L. M. Frutos, L. Gagliardi,
M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma,
P.- Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B.
Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta,
I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur,
A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart,
F. Zapata, R. Lindh:
“”Molcas 8: New
Capabilities for Multiconfigurational Quantum Chemical Calculations Across
the Periodic Table. J. Comput. Chem., 37, 506-541 (2015). - [104]
-
I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach,
J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru,
J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag,
L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell,
M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht,
G. Kovacevi\’c, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai,
J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell,
M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M.
Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar,
M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser,
T. A. Wesolowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel,
R. Lindh:
“”OpenMolcas: From
Source Code to Insight. J. Chem. Theory Comput., 15,
5925-5964 (2019). - [105]
-
H. Lischka, T. Müller, P. G. Szalay, I. Shavitt, R. M. Pitzer, R. Shepard:
“”Columbus – a program
system for advanced multireference theory calculations. WIREs Comput.
Mol. Sci., 1, 191-199 (2011). - [106]
-
H. Lischka, R. Shepard, I. Shavitt, R. M. Pitzer, M. Dallos, T. Müller, P. G.
Szalay, F. B. Brown, R. Ahlrichs, H. J. Böhm, A. Chang, D. C. Comeau,
R. Gdanitz, H. Dachsel, C. Ehrhardt, M. Ernzerhof, P. Höchtl, S. Irle,
G. Kedziora, T. Kovar, V. Parasuk, M. J. M. Pepper, P. Scharf, H. Schiffer,
M. Schindler, M. Schüler, M. Seth, E. A. Stahlberg, J.-G. Zhao,
S. Yabushita, Z. Zhang, M. Barbatti, S. Matsika, M. Schuurmann, D. R.
Yarkony, S. R. Brozell, E. V. Beck, , J.-P. Blaudeau, M. Ruckenbauer,
B. Sellner, F. Plasser, J. J. Szymczak: “”COLUMBUS, an ab initio
electronic structure program, release 7.0 (2012). - [107]
-
S. Yabushita, Z. Zhang, R. M. Pitzer:
“”Spin-Orbit
Configuration Interaction Using the Graphical Unitary Group Approach and
Relativistic Core Potential and Spin-Orbit Operators. J. Phys. Chem.
A, 103, 5791-5800 (1999). - [108]
-
S. Mai, T. Müller, P. Marquetand, F. Plasser, H. Lischka, L. González:
“”Perturbational Treatment
of Spin-Orbit Coupling for Generally Applicable High-Level Multi-Reference
Methods. J. Chem. Phys., 141, 074 105 (2014). - [109]
-
E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford,
O. Baseggio, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerritger,
L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson,
J. M. Dieterich, D. E. Ellis, M. van Faassen, A. Ghysels, A. Giammona,
S. J. A. van Gisbergen, A. Goez, A. W. Götz, S. Gusarov, F. E. Harris,
P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert,
J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko,
M. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M.
Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga,
S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post,
C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, J. I. Rodríguez,
P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot,
G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà,
S. M., M. Swart, D. Swerhone, G. te Velde, V. Tognetti, P. Vernooijs,
L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van
Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo, A. L. Yakovlev:
“”ADF2019, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam,
The Netherlands, https://www.scm.com. - [110]
-
“”TURBOMOLE V7.0, A development of University of Karlsruhe and
Forschungszentrum Karlsruhe GmbH (2015). - [111]
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R.
Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson,
H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino,
G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda,
J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven,
J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd,
E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand,
K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi,
M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross,
V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev,
A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin,
K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg,
S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz,
J. Cioslowski, , D. J. Fox: “”Gaussian 09, Revision A.1. Gaussian,
Inc.: Wallingford CT, 2009 (2009). - [112]
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R.
Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li,
M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts,
B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg,
D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng,
A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega,
G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa,
M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven,
K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J.
Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A.
Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C.
Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo,
R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B.
Foresman, D. J. Fox: “”Gaussian16 Revision A.03 (2016), gaussian
Inc. Wallingford CT. - [113]
-
F. Neese: “”Software update:
the ORCA program system, version 4.0. WIREs Comput. Mol. Sci.,
8, e1327 (2017). - [114]
-
T. Shiozaki: “”BAGEL:
Brilliantly Advanced General Electronic-structure Library. WIREs
Comput. Mol. Sci., 8, e1331 (2018). - [115]
-
G. A. Meek, B. G. Levine:
“”Evaluation of the
Time-Derivative Coupling for Accurate Electronic State Transition
Probabilities from Numerical Simulations. J. Phys. Chem. Lett.,
5, 2351-2356 (2014). - [116]
-
G. Granucci, M. Persico, A. Zoccante:
“”Including quantum
decoherence in surface hopping. J. Chem. Phys., 133,
134 111 (2010). - [117]
-
A. W. Jasper, D. G. Truhlar:
“”Improved
treatment of momentum at classically forbidden electronic transitions in
trajectory surface hopping calculations. Chem. Phys. Lett.,
369, 60 – 67 (2003). - [118]
-
C. Zhu, A. W. Jasper, D. G. Truhlar:
“”Non-Born-Oppenheimer
Trajectories with Self-Consistent Decay of Mixing. J. Chem. Phys.,
120 (2004). - [119]
-
C. Zhu, A. W. Jasper, D. G. Truhlar:
“”Non-Born-Oppenheimer
Liouville-von Neumann Dynamics. Evolution of a Subsystem Controlled by Linear
and Population-Driven Decay of Mixing with Decoherent and Coherent
Switching. J. Chem. Theory Comput., 1, 527-540 (2005). - [120]
-
H. Köppel, W. Domcke, L. S. Cederbaum: “”Multimode molecular
dynamics beyond the Born-Oppenheimer approximation. Adv. Chem. Phys.,
57, 59-246 (1984). - [121]
-
M. Barbatti, G. Granucci, M. Ruckenbauer, F. Plasser, J. Pittner, M. Persico,
H. Lischka: “”NEWTON-X: a package for Newtonian dynamics close to
the crossing seam, version 1.2. www.newtonx.org (2011). - [122]
-
P. Marquetand: Vectorial properties and laser control of molecular
dynamics. Ph.D. thesis, University of Würzburg (2007),
http://opus.bibliothek.uni-wuerzburg.de/volltexte/2007/2469/. - [123]
-
L. Verlet: “”Computer
Ëxperiments” on Classical Fluids. I. Thermodynamical Properties of
Lennard-Jones Molecules. Phys. Rev., 159, 98-103 (1967).